足球比赛

- 我们可以考虑枚举主队的进球数 i i i,则客队的进球数为 j j j,且 j < i jj<i时主队获胜,而主队赢 i i i球的概率为 p i ∗ ( 1 − p ) n − i p^{i}*(1-p)^{n-i} pi∗(1−p)n−i,客队赢 j j j球的概率为 q j ∗ ( 1 − q ) n − j q^{j}*(1-q)^{n-j} qj∗(1−q)n−j
- 则主队进哪 i i i场球又是任意的,我们可以得到如下柿子: a n s = ∑ i = 1 n ( p i ∗ ( 1 − p ) n − i ∗ C n i ∗ ∑ j = 0 i − 1 ( q j ∗ ( 1 − q ) n − j ∗ C n j ) ) ans=\sum^{n}_{i=1}({p^{i}*(1-p)^{n-i}*C_{n}^{i}*\sum^{i-1}_{j=0}(q^{j}*(1-q)^{n-j}*C^{j}_{n})}) ans=i=1∑n(pi∗(1−p)n−i∗Cni∗j=0∑i−1(qj∗(1−q)n−j∗Cnj))
- 很容易想到 n 2 n^{2} n2递推,但也很容易看出来第二项可以前缀和求
- 还有一个关键是推逆元,先递推出 i i i的逆元 i n v [ i ] inv[i] inv[i],再前缀积求出阶乘逆元 i n v [ i ] inv[i] inv[i]
- 注意溢出问题和空间限制
#include
using namespace std;
#define maxn 10000050
const long long mod = 1e9+7;
int inv[maxn];
long long n,jcn,p,q,inv_p1,inv_q1;
inline long long read_() {
long long x_=0,f_=1;char c_=getchar();
while(c_<'0'||c_>'9') {if(c_=='-') f_=-1;c_=getchar();}
while(c_>='0'&&c_<='9') {x_=(x_<<1)+(x_<<3)+c_-'0';c_=getchar();}
return x_*f_;
}
inline long long quick_pow_(long long a,long long b) {
long long ans=1;
while(b) {
if(b&1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans%mod;
}
inline void init_() {
inv[0] = inv[1] = 1;
for(int i = 2;i <= n; ++i) {
inv[i] = (long long) (mod-mod/i) * inv[mod%i] % mod;
}
for(int i = 2;i <= n; ++i) inv[i] = (long long) inv[i-1] * inv[i] % mod;
jcn=1;
for(int i = 2; i <= n; ++i) { jcn *= i ; jcn %= mod ; }
}
inline long long C_(int x) {
return jcn % mod * inv[x] % mod * inv[n-x] % mod ;
}
void readda_() {
n = read_();
init_();
long long x = read_(),y = read_();
long long z = quick_pow_(y,mod-2) %mod ;
p = x * z % mod ;
long long p_1 = (y-x) * z % mod;
x = read_();y = read_();
z = quick_pow_(y,mod-2) % mod ;
q = x * z % mod ;
long long q_1 = (y-x) * z % mod;
inv_p1 = quick_pow_(p_1,mod-2) % mod ;
inv_q1 = quick_pow_(q_1,mod-2) % mod ;
long long la_p1 = quick_pow_(p_1,n) % mod ;
long long la_q1 = quick_pow_(q_1,n) % mod ;
long long la_p=1,la_q = 1 ;
long long ans=0,sum = la_q1 % mod ;
for(int i=1;i<=n;++i) {
la_p = la_p % mod * p % mod;
la_p1 = la_p1 % mod *inv_p1 % mod;
if(p_1==0&&i==n) la_p1=1;
ans = ( ans % mod + la_p % mod * la_p1 % mod * C_(i) % mod * sum % mod ) % mod ;
la_q = la_q * q % mod ;
la_q1 = la_q1 * inv_q1 % mod;
sum = ( sum % mod + la_q % mod * la_q1 % mod * C_(i) % mod ) % mod ;
} printf("%lld",ans % mod);
}
int main( ) {
readda_();
return 0;
}
文明
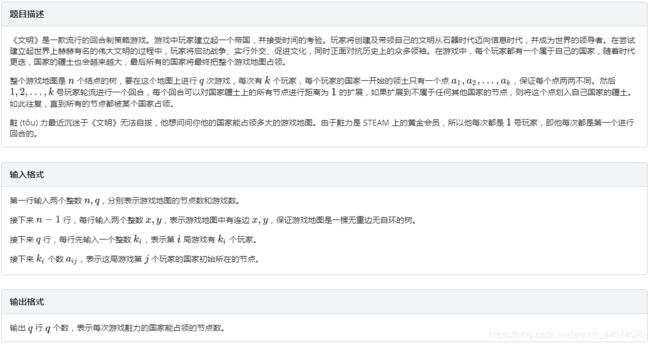
- 暴力 b f s 48 bfs48 bfs48分 c o d e code code
#include
using namespace std;
#define maxn 500050
int n,m,k,a[maxn],b[maxn],sze=0,head[maxn];
struct edge {
int v,nxt;
}e[maxn<<1];
inline int read_() {
int x_=0,f_=1;char c_=getchar();
while(c_<'0'||c_>'9') {if(c_=='-') f_=-1;c_=getchar();}
while(c_>='0'&&c_<='9') {x_=(x_<<1)+(x_<<3)+c_-'0';c_=getchar(); }
return x_*f_;
}
inline void init_() {
freopen("civilization.in","r",stdin);
freopen("civilization.out","w",stdout);
}
inline void add_(int u,int v) {
e[++sze].v=v;
e[sze].nxt=head[u];
head[u]=sze;
}
inline void solve_() {
queue<int>q;
for(int i=1;i<=k;++i) q.push(b[i]);
int ans=0;
while(!q.empty()) {
int u=q.front();q.pop();
if(a[u]==1) ++ans;
for(int i=head[u];~i;i=e[i].nxt) {
int v=e[i].v;
if(a[v]!=0) continue;
a[v]=a[u];
q.push(v);
}
}
printf("%d\n",ans);
}
void readda_() {
n=read_();m=read_();
int x,y;memset(head,-1,sizeof(head));
for(int i=1;i<n;++i) {
x=read_();y=read_();
add_(x,y);add_(y,x);
}
while(m--) {
k=read_();
for(int i=0;i<=n;++i) a[i]=0;
for(int i=1;i<=k;++i) {
x=read_();
a[x]=i;b[i]=x;
}
bool flag=true;
for(int i=head[b[1]];~i;i=e[i].nxt) {
int v=e[i].v;
if(!a[v]) {flag=false;break;}
}
if(flag) {printf("1\n");continue;}
solve_();
}
}
int main() {
init_();
readda_();
return 0;
}
- 其实很容易想到树链剖分来做,每次设当前的一号节点为假根,将线段树区间全部赋为 1 1 1,.每次考虑 r o o t root root与 u u u的链,先求出他们的 l c a lca lca,如果中点在靠右边的 u u u这边,先跳到 u u u这个点 m i d mid mid,则 r o o t root root无法对 m i d mid mid以及其子树染色,于是我们线段树将这段区间赋为 0 0 0。另一种情况,当 m i d mid mid在靠近假根 r o o t root root的一侧,则也是先跳到 m i d mid mid这个点,可以发现,这时只能给 m i d mid mid及其子树染色为 1 1 1,于是我们将除了这个子树的其他区间全部赋为 0 0 0。最后求和一下。
- 注意求 L C A LCA LCA和 j u m p jump jump的细节
- 思考一个问题 ? ? ? ??? ???
#include
using namespace std;
#define maxn 500050
#define lson l,mid,nod<<1
#define rson mid+1,r,nod<<1|1
int seg[maxn],rev[maxn],top[maxn],root,n,m,sze[maxn],f[maxn],dep[maxn],son[maxn],tot=0,head[maxn];
struct edge {
int v,nxt;
}e[maxn<<1];
struct node {
int sum,la;
node(){la=-1;}
}tr[maxn<<2];
inline int read_() {
int x_=0,f_=1;char c_=getchar();
while(c_<'0'||c_>'9') {if(c_=='-') f_=-1;c_=getchar();}
while(c_>='0'&&c_<='9') {x_=(x_<<1)+(x_<<3)+c_-'0';c_=getchar();}
return x_*f_;
}
inline void add_(int u,int v) {
e[++tot].v=v;
e[tot].nxt=head[u];
head[u]=tot;
}
void dfs_1_(int u,int fa) {
dep[u]=dep[fa]+1;
f[u]=fa;sze[u]=1;
for(int i=head[u];~i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa) continue;
dfs_1_(v,u);
sze[u]+=sze[v];
if(sze[v]>sze[son[u]]) son[u]=v;
}
}
void dfs_2_(int u,int fa) {
if(son[u]) {
seg[son[u]]=++seg[0];
top[son[u]]=top[u];
rev[seg[0]]=son[u];
dfs_2_(son[u],u);
}
for(int i=head[u];~i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa) continue;
if(!top[v]) {
seg[v]=++seg[0];
top[v]=v;
rev[seg[0]]=v;
dfs_2_(v,u);
}
}
}
inline int LCA_(int u,int v) {
while(top[u]!=top[v]) {
if(dep[top[u]]<dep[top[v]]) swap(u,v);
u=f[top[u]];
}
if(dep[u]<dep[v]) return u;
else return v;
}
inline int jump_(int u,int v) {
while(dep[u]-dep[top[u]]+1<=v) {
v-=dep[u]-dep[top[u]]+1;
u=f[top[u]];
}
return rev[seg[u]-v];
}
inline void xiugai_(int l,int r,int nod,int v) {
tr[nod].sum = (r-l+1) * v;
tr[nod].la = v;
}
inline void pushup_(int nod) {
tr[nod].sum = tr[nod<<1].sum + tr[nod<<1|1].sum ;
}
void update_(int l,int r,int nod,int LL,int RR,int v) {
if(LL<=l&&RR>=r) {
xiugai_(l,r,nod,v);
return ;
}
int mid=(l+r)>>1;
if(tr[nod].la!=-1) {xiugai_(lson,tr[nod].la);xiugai_(rson,tr[nod].la);tr[nod].la=-1;}
if(LL<=mid) update_(lson,LL,RR,v);
if(RR>mid) update_(rson,LL,RR,v);
pushup_(nod);
}
void readda_() {
n=read_();m=read_();
int x,y;memset(head,-1,sizeof(head));
for(int i=1;i<n;++i) {
x=read_();y=read_();
add_(x,y);add_(y,x);
}
dep[0]=0;dfs_1_(1,0);
seg[0]=seg[1]=rev[1]=top[1]=1;
dfs_2_(1,0);
int cnt,lca,lf,ri,dis,mid;
while(m--) {
cnt=read_();root=read_();
update_(1,n,1,1,n,1);
for(int i=2;i<=cnt;++i) {
x=read_();
lca=LCA_(x,root);
lf=dep[root]-dep[lca]+1;
ri=dep[x]-dep[lca]+1;
dis=lf+ri-1;
mid=dis>>1;
if(mid<ri) {
y=jump_(x,mid-1);
update_(1,n,1,seg[y],seg[y]+sze[y]-1,0);
}
else {
y=jump_(root,dis-mid-1);
update_(1,n,1,1,seg[y]-1,0);
update_(1,n,1,seg[y]+sze[y],n,0);
}
}
printf("%d\n",tr[1].sum);
}
}
int main() {
freopen("a.txt","r",stdin);
readda_();
return 0;
}
贪玩蓝月
- 先考虑不删除的情况,我们可以使用背包维护答案:,定义 f [ i ] [ j ] f[i][j] f[i][j]表示前 i i i个物品,体积之和对 m o d mod mod取模的模数为 j j j时的最大值。则: f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ ( ( j − w ) % m o d + m o d ) % m o d ) ] + v ) f[i][j]=max(f[i-1][j],f[i-1][((j-w)\%mod+mod)\%mod)]+v) f[i][j]=max(f[i−1][j],f[i−1][((j−w)%mod+mod)%mod)]+v)
- 可以发现,如果我们双端队列来维护数据的话,则弹出一个队首元素就需要重新维护整个 f f f数组。考虑能不能换个数据结构?用两个栈来维护,第一个栈顶维护较前端的元素,第二个栈维护较后端的元素。
- 考虑查询如何操作?相当于对于右边栈的 f [ r t o p ] [ i ] f[r_{top}][i] f[rtop][i]找一个 f [ l t o p ] [ j ] f[l_{top}][j] f[ltop][j]满足 l < = ( i + j ) % m o d < = r l<=(i+j)\%mod<=r l<=(i+j)%mod<=r,并且使 f [ r t o p ] [ i ] + f [ l t o p ] [ j ] f[r_{top}][i]+f[l_{top}][j] f[rtop][i]+f[ltop][j]最大。每次对于右栈的 f [ r t o p ] [ i ] f[r_{top}][i] f[rtop][i],如何求出合理的左栈的 j j j区间,可以发现,我们需要找出 x x x满足: l < = ( i + x ) % m o d < = r l<=(i+x)\%mod<=r l<=(i+x)%mod<=r,根据同余的性质,不难得出: ( l − i ) % m o d < = x < = ( r − i ) % m o d (l-i)\%mod<=x<=(r-i)\%mod (l−i)%mod<=x<=(r−i)%mod
- 于是我们对于每次的 f [ r t o p ] [ i ] f[r_{top}][i] f[rtop][i],都到左栈对用的区间 x 属 于 [ l − i , r − i ] x属于[l-i,r-i] x属于[l−i,r−i]去找最大的 f [ l t o p ] [ x ] f[l_{top}][x] f[ltop][x],对于所有的取个最大值就是答案,如果答案小于 0 0 0,输出 − 1 -1 −1
- 注意:有可能会出现 ( l − i ) > ( r − i ) (l-i)>(r-i) (l−i)>(r−i)的情况,这个时候查询区间应该是 [ 0 , r − i ] [0,r-i] [0,r−i]和 [ l − i , m o d ) [l-i,mod) [l−i,mod)
#include
using namespace std;
#define maxm 50050
#define maxp 550
#define INF 1000000000000000
#define lson l,mid,nod<<1
#define rson mid+1,r,nod<<1|1
int m,mod;
long long tr[maxp<<2];
pair<int,int>d[maxm];
char s[5];
struct stack_ {
int top;
long long f[maxm][maxp];
pair<int,int>a[maxm];
inline void init_() {
top = 0;f[0][0] = 0;
for(int i=1;i<mod;++i) f[0][i] = -INF;
}
inline void push_(int w,int v) {
a[++top] = make_pair(w,v);
for(int i=0;i<mod;++i)
f[top][i]=max(f[top-1][i],f[top-1][((i-w)%mod+mod)%mod]+v);
}
} L , R ;
inline int read_() {
int x_=0,f_=1;char c_=getchar();
while(c_<'0'||c_>'9') {if(c_=='-') f_=-1;c_=getchar();}
while(c_>='0'&&c_<='9') {x_=(x_<<1)+(x_<<3)+c_-'0';c_=getchar();}
return x_*f_;
}
inline void rebuild_() {
int cnt = 0;
for(int i=L.top;i>=1;--i) d[++cnt] = L.a[i];
for(int i=1;i<=R.top;++i) d[++cnt] = R.a[i];
L.init_();R.init_();
int mid = cnt >> 1;
for(int i=mid;i>=1;--i) L.push_(d[i].first,d[i].second);
for(int i=mid+1;i<=cnt;++i) R.push_(d[i].first,d[i].second);
}
void build_(int l,int r,int nod) {
if(l==r) {
tr[nod] = L.f[L.top][l];
return ;
}
int mid = (l+r) >> 1;
build_(lson);build_(rson);
tr[nod] = max( tr[nod<<1] , tr[nod<<1|1] ) ;
}
long long query_(int l,int r,int nod,int LL,int RR) {
if(LL<=l&&RR>=r) return tr[nod] ;
int mid = (l+r) >> 1;
long long ans = -INF;
if(LL<=mid) ans = query_(lson,LL,RR);
if(RR>mid) ans = max(ans,query_(rson,LL,RR));
return ans ;
}
inline void solve_(int x,int y) {
build_(0,mod,1);
int l,r;
long long ans = -1 , maxd ;
for(int i=0;i<mod;++i) {
if(R.f[R.top][i]<0) continue;
l = ( (x-i) % mod + mod ) % mod;
r = ( (y-i) % mod + mod ) % mod;
if(l<=r) maxd = query_(0,mod,1,l,r);
else {
maxd = query_(0,mod,1,l,mod-1);
maxd = max( maxd , query_(0,mod,1,0,r) );
}
ans = max( ans , maxd + R.f[R.top][i] ) ;
}
printf("%lld\n",ans) ;
}
void readda_() {
read_();
m=read_();mod=read_();
L.init_();R.init_();
int x,y;
while(m--) {
scanf("%s",s);
if(s[0]=='I'&&s[1]=='F') {
x=read_();y=read_();
L.push_(x,y);
}
else if(s[0]=='I'&&s[1]=='G') {
x=read_();y=read_();
R.push_(x,y);
}
else if(s[0]=='D'&&s[1]=='F') {
if(!L.top) rebuild_();
if(!L.top) --R.top;
else --L.top;
}
else if(s[0]=='D'&&s[1]=='G') {
if(!R.top) rebuild_();
if(!R.top) --L.top;
else --R.top;
}
else if(s[0]=='Q') {
x=read_();y=read_();
solve_(x,y);
}
}
}
int main() {
freopen("a.txt","r",stdin);
readda_();
return 0;
}

