Pytorch入门+实战系列二：Pytorch基础理论和简单的神经网络实现

Pytorch官方文档：https://pytorch.org/docs/stable/torch.html?

1. 写在前面

今天开始，兼顾Pytorch学习， 如果刚刚接触深度学习并且想快速搭建神经网络完成任务享受快感，当然是Keras框架首选，但是如果想在深度学习或人工智能这条路上走的更远，只有Keras就显得有点独木难支，这时候我们需要一个更加强大的框架，这里我想学习Pytorch，它代码通俗易懂，接近Python原生，学起来也容易一些，所以接下来会整理自己在快速入门Pytorch道路上的所见所得，这个系列会有8篇理论+实战的文章，也是我正在学习的B站上的Pytorch入门实战课程，我会把学习过程的笔记和所思所想整理下来，也希望能帮助更多的人进军Pytorch。想要快速学习Pytorch，最好的秘诀就是手握官方文档，然后不断的实战加反思。

如果想真正的理解知识，那么最好的方式就是用自己的话再去描述一遍， 通过这个系列，我相信能够打开Pytorch的大门，去眺望一个新的世界。

今天是课程的第一节课，在这一节课中，我们会学习Pytorch的基本理论知识并进行演示，不是面面俱到，只是点到为止（要善于查官方文档）。 然后我们会先用numpy搭建一个简单的两层神经网络进行热身（这里会带你领略前向传播，反向传播的细节计算），之后，我们会用Pytorch一步一步的替代numpy里面的步骤，最后形成一个Pytorch版本的两层神经网络，在这个过程中，你会亲身体会到Pytorch的强大。 完成上面的任务之后，就应该学会搭建简单的神经网络了，那么就小试牛刀一下，搭建一个神经网络并教会他玩一个简单的游戏！

分享大纲如下：

• Pytorch的基本知识
• 热身： numpy实现简单的两层神经网络（自己实现神经网络前向，反向传播，有利于理解神经网络的计算原理）
• Pytorch一步一步的替代上面的网络
• 教你的网络玩FizzBuzz小游戏

OK， let’s go!

2. Pytorch的基础知识

2.1 什么是Pytorch？

PyTorch是一个基于Python的科学计算库，它有以下特点:

• 类似于NumPy，但是它可以使用GPU
• 可以用它定义深度学习模型，可以灵活地进行深度学习模型的训练和使用

2.2 Tensors

Tensor类似与NumPy的ndarray，唯一的区别是Tensor可以在GPU上加速运算。

下面实际演练一下Tensor的一些构造方式：

# 导入Pytorch
import torch

# 构造一个未初始化的5 * 3的矩阵
x = torch.empty(5, 3)    # 5行3列的未初始化Tensor

# 构造一个随机初始化的矩阵
x = torch.rand(5, 3)  # 5行3列的随机初始化Tensor， 都在0-1之间

# 构造一个全部为0， 类型为long的矩阵
x = torch.zeros(5, 3, dtype=torch.long)   # dtype属性可以指定类型 5行3列的全0tensor

# 从数据中直接构造tensor
x = torch.tensor([5.5, 3])   # tensor([5.5000, 3.0000])

# 可以从一个已有的Tensor构建一个tensor
# 这些方法会重用原来的Tensor的特征，例如数据类型，除非提供新的数据
x = x.new_ones(5, 3, dtype=torch.double)  # 5行3列全1Tensor
y = torch.randn_like(x, dtype=torch.float)  # y也是5行3列

# 得到Tensor的形状
x.size()
x.shape()

2.3 演示一些简单运算

# 加法运算
x = x.new_ones(5, 3, dtype=torch.double)  # new_* methods take in sizes
y = torch.rand(5, 3)
print(x+y)
print(torch.add(x,y))  # 另一种加法的写法

# 加法： 把输出作为一个变量
result = torch.empty(5,3)
torch.add(x, y, out=result)
print(result)

# in-place加法
y.add_(x)
print(y)   # 这时候是y本身加上了x

"""任何in-place的运算都会以``_``结尾。举例来说：``x.copy_(y)``, ``x.t_()``, 会改变 ``x``"""

各种类似NumPy的indexing都可以在PyTorch tensor上面使用。

# 切片
print(x[:,1])

# Resizing:如果希望resize/reshape一个tensor，可以使用torch.view
x = torch.randn(4,4)
y = x.view(16)   # 相当与成了一维的了
z = x.view(-1, 8)  # the size -1 is inferred from other dimensions

# 如果有一个只有一个元素的tensor，使用.item()方法可以把里面的value变成Python数值
x = torch.randn(1)
print(x)   # tensor([0.4276])
print(x.item())  # 0.4276

更多阅读

各种Tensor operations, 包括transposing, indexing, slicing,mathematical operations, linear algebra, random numbers在
.

2.4 Numpy和Tensor之间的转化

• 在Torch Tensor和Numpy array之间的转化非常容易
• Torch Tensor和Numpy array会共享内存，所以改变其中一项也会改变另一项
• 把Torch Tensor转变成Numpy array 函数 张量.numpy()
• Numpy array 转变成Torch Tensor 用 torch.from_numpy(array)

"""Torch Tensor 转变成Numpy array"""
a = torch.ones(5)
print(a)   # tensor([1., 1., 1., 1., 1.])
b = a.numpy()
print(b)   # [1. 1. 1. 1. 1.]

# 改变numpy里面的数值
a.add_(1)
print(a)    # tensor([2., 2., 2., 2., 2.])
print(b)     # [2. 2. 2. 2. 2.]

"""Numpy array转成Torch Tensor"""
a = np.ones(5)
b = torch.from_numpy(a)
print(a)   # [1. 1. 1. 1. 1.]
print(b)    # tensor([1., 1., 1., 1., 1.])

np.add(a, 1, out=a)  # 这个是在原内存上操作
print(a)  # [2. 2. 2. 2. 2.]
print(b)   # tensor([2., 2., 2., 2., 2.])  

a = a + 1   # 这个是新开辟了一块空间，注意和上面区分
print(a)   # [3. 3. 3. 3. 3.]
print(b)   # tensor([2., 2., 2., 2., 2.])  

所有的CPU上的Tensor都支持转成numpy或者从numpy转成Tensor

2.5 CUDA Tensors

如果有GPU的话，我们可以使用.to方法，Tensor被移动到别的device上去

if torch.cuda.is_available():
	device = torch.device("cuda")   # 一个GPU对象
	y = torch.ones_like(x, device=device)
	x = x.to(device)   # x从CPU移到GPU
	z = x + y
	print(z)      # 这是在GPU上完成的加法运算，结果存到z
	print(z.to("cpu", toch.double)  # 把z从GPU移到CPU

一个Tensor在GPU上，是无法直接转成numpy的， 需要先转到CPU上

# y.data.numpy()    这个会报错
y.to("cpu").data.numpy()

把模型搬到GPU上 (如果想用GPU，需要把东西搬到GPU上去)

model = model.cuda()

3. 热身： 用numpy实现两层神经网络

一个全连接ReLU神经网络，一个隐藏层，没有bias。用来从x预测y，使用L2 Loss。

• $hidden=W_{1}X$
• $a=max(0,h)$
• $y_{hat}=W_{2}a$

这一实现完全使用numpy来计算前向神经网络，loss，和反向传播。

• forward pass
• loss
• backward pass

numpy ndarray是一个普通的n维array。它不知道任何关于深度学习或者梯度(gradient)的知识，也不知道计算图(computation graph)，只是一种用来计算数学运算的数据结构。

我们实现的神经网络长下面这个样子，我已经标注好了参数的维度，并且也把计算过程写了一下：

下面我们根据上面的计算过程，用numpy一步步的实现这个网络：

# 定义样本数，输入层，隐藏层，输出层的参数
N, D_in, H, D_out = 64, 1000, 100, 10

# 创造训练样本x,y  这里随机产生
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)

# 随机初始化参数w1， w2
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)

# 下面就是实现神经网络的计算过程
learning_rate = 1e-6
epochs = 500
for epoch in range(epochs):
	# 前向传播
	h = x.dot(w1)
	h_relu = np.maximum(h, 0)
	y_pred = h_relu.dot(w2)
	
	# 计算损失
	loss = np.square(y_pred-y).sum()
	print(epoch, loss)
	
	# 反向传播
	# w2的梯度
	grad_y_pred = 2.0 * (y_pred-y)
	grad_w2 = h_relu.T.dot(grad_y_pred)
	# w1的梯度
	grad_h_relu = grad_y_pred.dot(w2.T)
	grad_h = grad_h_relu.copy()
	grad_h[h<0] = 0
	grad_w1 = x.T.dot(grad_h)
	
	# 更新参数
	w1 -= learning_rate * grad_w1
	w2 -= learning_rate * grad_w2

这样就完成了numpy手写两层神经网络的过程。可以运行一下，会发现loss值随着迭代次数的增加，会减小。

但是你会发现，上面这个过程很复杂的，尤其是反向传播那块，得需要自己小心翼翼的求导数。

所以，我们下面看看Pytorch版本是如何一步一步的取代numpy版本的代码的。（你会享受下面的过程 ）

4. Pytorch一步一步的替代上面的网络

4.1 Pytorch: Tensors

这次我们使用PyTorch tensors来创建前向神经网络，计算损失，以及反向传播。(也就是先把numpy的写法，换成tensor的写法）

一个PyTorch Tensor很像一个numpy的ndarray。但是它和numpy ndarray最大的区别是，PyTorch Tensor可以在CPU或者GPU上运算。如果想要在GPU上运算，就需要把Tensor换成cuda类型。

# 定义输入，中间，输出层的个数和上面一样
N, D_in, H, D_out = 64, 1000, 100, 10

# 随机创建训练数据   这里的np.random.randn换成Pytorch的写法
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 初始化权重
w1 = torch.randn(D_in, H)
w2 = torch.randn(H, D_out)

#下面训练网络，和上面版本过程一致，只不过有些地方换成了Pytorch的写法而已
learnint_rate = 1e-6
epochs = 500

for epoch in range(epochs):
	# 前向传播   矩阵的点乘这里换成了mm
	h = x.mm(w1)
	h_relu = h.clamp(min=0)     # 这个张量里面换成了clamp操作，来保证元素取值控制在区间内
	y_pred = h_relu.mm(w2)

	# 计算损失   这里要使用张量的item()取出值来
	loss = (y_pred-y).pow(2).sum().item()
	print(epoch, loss)
	
	# 反向传播, 转置操作换成了t(). copy()换成了clone()
	# compute the gradient
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h_relu.t().mm(grad_y_pred)
    grad_h_relu = grad_y_pred.mm(w2.T)
    grad_h = grad_h_relu.clone()
    grad_h[h<0] = 0
    grad_w1 = x.t().mm(grad_h)
	
	# 更新参数
	w1 -= learning_rate  * grad_w1
    w2 -= learning_rate * grad_w2

这一块，没有太大的改变，只不过是把numpy的数组操作，换成了相应的张量运算，下面我们看看Pytorch一个强大的地方：自动求导，这时候你会发现代码简洁了很多。

4.2 Pytorch: Tensor 和 autograd

PyTorch的一个重要功能就是autograd，也就是说只要定义了forward pass(前向神经网络)，计算了loss之后，PyTorch可以自动求导计算模型所有参数的梯度。

一个PyTorch的Tensor表示计算图中的一个节点。如果x是一个Tensor并且x.requires_grad=True那么x.grad是另一个储存着x当前梯度(相对于一个scalar，常常是loss)的向量。

我们再改动上面代码之前，先看一个简单的自动求导的例子：

x = torch.tensor(1., requires_grad=True)
w = torch.tensor(2., requires_grad=True)
b = torch.tensor(3., requires_grad=True)

y = w * x + b

y.backward()      # 求导只需这一句话

print(w.grad)    # tensor(1.)   也就是x
print(b.grad)    # tensor(1.)    b求导本身为1
print(x.grad)     # tensor(2.)   也就是w

好了，我们尝试引进Pytorch的自动求导机制

# 这里依然不变
N, D_in, H, D_out = 64, 1000, 100, 10   # N表示训练数据的个数， D_in表示输入的特征数 H是中间层，

# 随机创建一下训练数据   这里也不变
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 这里随机初始化权重，需要requires_grad=True  需要保留梯度
w1 = torch.randn(D_in, H, requires_grad=True)
w2 = torch.randn(H, D_out, requires_grad=True)

# 开始神经网络计算
learning_rate = 1e-6
epoches = 500

for epoch in range(epoches):
	# 前向传播，简单精简一下
	y_pred = x.mm(w1).clamp(min=0).mm(w2)
	
	# 计算损失和上面一样
	loss = (y_pred-y).pow(2).sum()
	print(epoch, loss.item())

	# 反向传播  这里我们使用自动求导机制，一句话就搞定
	loss.backward()

	# 更新参数，注意，这时候我们不需要计算w的梯度了，所以得关上梯度计算
	with torch.no_grad():
		w1 -= learning_rate * w1.grad
		w2 -= learning_rate * w2.grad
		
		# 这里还有个关键的地方，就是Pytorch的求导机制是默认采用累加的方式，也就是每一代求完梯度，不会自动清零，下一代的梯度是前一代加上本一代的梯度，这时候就错了，所以我们得自动每一代之后，梯度清零
		w1.grad.zero_()
		w2.grad.zero_()

好了，这个版本的两层神经网络计算，就简单一些了，反向传播过程只需要一句话就搞定了。

但是那两个小问题要注意：

• 更新参数的时候，我们如果不需要求参数的梯度，我们应该关上梯度计算，这样会节省内存空间
• Pytorch的求导机制默认是累加，我们需要每一代之后，参数的导数给它清零

好了，我们已经知道了Pytorch的自动求导机制，.backward()。 这时候，会把前面声明时需要求导的参数的导数保存在相应的.grad变量中，我们可以直接使用。 下面我们看还能不能精简，哈哈，能的，前向传播也可以通过模型的方式。

4.3 Pytorch: nn

这次我们使用PyTorch中nn这个库来构建网络。 用PyTorch autograd来构建计算图和计算gradients， 然后PyTorch会帮我们自动计算gradient。

# 这次先导入nn的库
import torch.nn as nn

# 定义输入，中间，输出层的单元数量
N, D_in, H, D_out = 64, 1000, 100, 10   # N表示训练数据的个数， D_in表示输入的特征数 H是中间层，

# 创建训练数据，和上面一样
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 这里我们不定义w了，使用nn建立一个模型进行前向传播的过程计算,这里建模型，就类似于Keras的Sequential了，非常方便
model = torch.nn.Sequential(
	torch.nn.Linear(D_in, H),
	torch.nn.ReLU(),
	torch.nn.Linear(H, D_out)
)

# 这里我们初始化一下子我们的参数(这一步非关键，但是初始化完了之后发现训练的效果好，你可以对比看看，不加这两句的话增大学习率也可以)
torch.nn.init.normal_(model[0].weight)
torch.nn.init.normal_(model[1].weight)

# 开始神经网络的计算
loss_fn = nn.MSELoss(reduction='sum')
learning_rate = 1e-6

for it in range(500):
	# 前向传播，建立模型即可, 也是一句话搞定
	y_pred = model(x)
	
	# 计算损失  这里的损失函数用Pytorch版
	loss = loss_fn(y_pred, y)
	print(it, loss.item())

	# 参数导数归0，然后反向传播，这里会计算所有需要求导参数的梯度保存到一个参数列表中
	model.zero_grad()
	loss.backward()

	# 更新参数, 这个地方注意，使用model之后，反向传播得到的参数会在一个参数列表中model.parameters() 我们需要在这里面求出参数来进行改变
	with torch.no_grad():
		for param in model.parameters():  # param (tensor, grad)的形式
			param -= learning_rate * param.grad

这一个版本中，我们使用了Pytorch里面的nn模型，替换了numpy手写的前向传播部分，然后用换了一下损失函数计算方式，然后借助Pytorch的自动求导机制完成了反向传播部分。我们还有差一个地方，就成了全自动模式，那就是更新参数了。下一步我们把这个也换掉。

4.4 Pytorch:optim

这一次我们不再手动更新模型的weights,而是使用optim这个包来帮助我们更新参数。 optim这个package提供了各种不同的模型优化方法，包括SGD+momentum, RMSProp, Adam等等。

# 定义输入输出层的个数 和上面一样
N, D_in, H, D_out = 64, 1000, 100, 10

# 创造训练集
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 定义模型
model = torch.nn.Sequential(
	torch.nn.Linear(D_in, H),
	torch.nn.ReLU(),
	torch.nn.Linear(H, D_out)
)

# 如果训练效果不好，也可以加上这两句试试，深度学习有点玄学
#torch.nn.init.normal_(model[0].weight)
#torch.nn.init.normal_(model[1].weight)

# 开始神经网络的计算,但是这里我们使用优化器帮我们更新参数
learning_rate = 1e-6
loss_fn = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

for it in range(500):
	# 前向传播
	y_pred = model(x)

	# 计算损失
	loss = loss_fn(y_pred, y)
	print(it, loss.item())

	# 梯度清零, 然后反向传播
	optimizer.zero_grad()
	loss.backward()

	# 更新参数，这里只需要一句话
	optimizer.step()

好了，我们基本上大功告成，已经把numpy的两层神经网络的计算换成了Pytorch版本了，换完之后，我们会发现，原来我们需要的复杂运算，在Pytorch里面只需要几句话就搞定了。

简单总结一下上面的替换过程：

• 首先，我们把把numpy的计算形式换成了tensor的计算形式，形成第一个版本
• 然后，我们使用Pytorch的自动求导机制loss.backward()替换了反向传播过程，形成了第二个版本
• 然后，我们使用Pytorch的nn模型，建立model，替换了前向传播，并且调用了Pytorch写好的损失函数替换了计算损失的过程
• 最后，我们使用optim库里面的优化函数，替换了更新参数的过程

这样，Pytorch的两层神经网络完毕。

但是，仍然有一个问题，就是nn.Sequential就类似于Keras的Sequential，只能类似堆积木般的一层一层往上堆，线性模块。不太擅长搭建复杂的模型，所以Keras那边有一个model系列。 而对应Pytorch里面，我们也有对应的解决办法，那就是自定义nn.Modules模型。 我们接着往下看。

4.5 Pytorch: 自定义nn Modules

我们可以定义一个模型，这个模型继承自nn.Module类。如果需要定义一个比Sequential模型更加复杂的模型，就需要定义nn.Module模型。

# 我们定义一个两层的神经网络类，这个继承与nn.Module模块
class TwoLayerNet(torch.nn.Module):
	
	# 定义成员层
	def __init__(self, D_in, H, D_out):
		super(TwoLayerNet, self).__init__()
		self.liner1 = torch.nn.Linear(D_in, H)
		self.linear2 = torch.nn.Linear(H, D_out)
	
	# 定义前向传播
	def forward(self, x):
		h_relu = self.linear1(x).clamp(min=0)
		y_pred = self.linear2(h_relu)
		return y_pred

# 这样就定义了一个二层神经网络的类

N, D_in, H, D_out = 64, 1000, 100, 10

x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 定义一个模型
model = TwoLayer(D_in, H, D_out)

# 开始计算神经网络
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)

for it in range(500):
	# 前向传播
	y_pred = model(x)

	# 计算损失
	loss = criterion(y_pred, y)
	print(it, loss)

	# 反向传播, 更新参数
	optimizer.zero_grad()
	loss.backward()
	optimizer.step()

看完这个，你会发现，这啥？ 这不基本上啥也没改吗？ 无非就是把model的定义写成了一个类的形式， 看起来还不如nn.Sequential搭建起来简单，但是，我们发现了吗？ 这个写法更加灵活了，我们可以在类里面的forward函数中，自定义任何复杂结构的神经网络。 而前面的Sequential，灵活性不够，这个就类似于Keras的Sequential和Model这两种方式的定义神经网络的方法。 Pytorch这里也是给出了两种，一般简单的网络，Sequential就可以搞定，但是复杂的，我们还得用下面这个写法，所以习惯了就好。 如果对于Keras好奇，我也正在写关于Keras的一个系列，那个读完之后会有一种修仙的快感

好了， 我们已经会用Pytorch搭建神经网络了，下面亲手搭一个神经网络，教你的神经网络玩个游戏吧，看看表现咋样？

5. 教你的网络玩FizzBuzz小游戏

FizzBuzz是一个简单的小游戏。游戏规则如下：从1开始往上数数，当遇到3的倍数的时候，说fizz，当遇到5的倍数，说buzz，当遇到15的倍数，就说fizzbuzz，其他情况下则正常数数。

这个就类似于我们酒席上玩的那个数数游戏，只不过是个简化版，你看到规则之后，转念一想，这还不简单，分分钟写个程序，按照这个规则从1-1000遍历，遇到3的倍数，输出fizz，遇到5的倍数，输出buzz， 遇到15的倍数，输出fizzbuzz。其他情况正常输出。 哈哈哈，你真这么写，我也无语，但那不是你机器玩的，那是你玩的， 我们的目的是搭建一个网络，让网络玩这个游戏。 看看网络怎么玩？

分下面几个步骤：

1. 我们先写一个编码函数，就是传进一个数，如果是3的倍数，返回1， 是5的倍数，返回2， 是15的倍数，返回3，其他情况返回0，这个好写吧：

def fizz_buzz_endode(i):
	if i % 15 == 0: return 3
	elif i % 5 == 0: return 2
	elif i % 3 == 0: return 1
	else: return 0

2. 我们写一个解码函数，就是根据上面的返回数，我们得到fuzz,buzz还是别的

def fizz_buzz_decode(i, prediction):
	return [str(i), "fizz", "buzz", "fizzbuzz"][prediction]

3. 我么定义模型的输入，由于我们是数数，但是训练模型的时候，我们得把数转换成特征的方式网络才能懂，所以这里采用二进制的编码形式

import numpy as np
import torch

NUM_DIGITS = 10

def binary_encode(i, num_digits):
	return np.array([i >> d & 1 for d in range(num_digits)]

# 准备训练集
trX = torch.Tensor([binary_encode(i, NUM_DIGITS) for i in range(101, 2 ** NUM_DIGITS)])
trX = torch.Tensor([fizz_buzz_encode(i) for i in range(101, 2 ** NUM_DIGITS)])

4. 然后用Pytorch定义模型
   这实际上是一个4分类的问题，就是输入数字，看看模型输出的是哪一个类别。

NUM_HIDDEN = 100
model = torch.nn.Sequential(
	torch.nn.Linear(NUM_DIGITS, NUM_HIDDEN),
	torch.nn.ReLU(),
	torch.nn.Linear(NUM_HIDDEN, 4)
)

5. 模型的训练

• 为了让我们的模型学会FizzBuzz这个游戏，我们需要定义一个损失函数，和一个优化算法。
• 这个优化算法会不断优化（降低）损失函数，使得模型的在该任务上取得尽可能低的损失值。
• 损失值低往往表示我们的模型表现好，损失值高表示我们的模型表现差。
• 由于FizzBuzz游戏本质上是一个分类问题，我们选用Cross Entropyy Loss函数。
• 优化函数我们选用Stochastic Gradient Descent。

loss_fn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr = 0.05)
BATCH_SIZE = 128

for epoch in range(10000):
	for start in range(0, len(trX), BATCH_SIZE):
		end = start + BATCH_SIZE
		batchX = trX[start:end]
		batchY = trY[start:end]

		y_pred = model(batchX)
		loss = loss_fn(y_pred, batchY)

		optimizer.zero_grad()
		loss.backward()
		optimizer.step()
	
	loss = loss_fn(model(trX),trY).item()
	print(epoch, loss)

6. 最后用我们训练好的模型尝试在1-100上玩FIZZBUZZ游戏

testX = torch.Tensor([binary_encode(i, NUM_DIGITS) for i in range(1, 101)])
with torch.no_grad():
    testY = model(testX)
predictions = zip(range(1, 101), list(testY.max(1)[1].data.tolist()))

print([fizz_buzz_decode(i, x) for (i, x) in predictions])

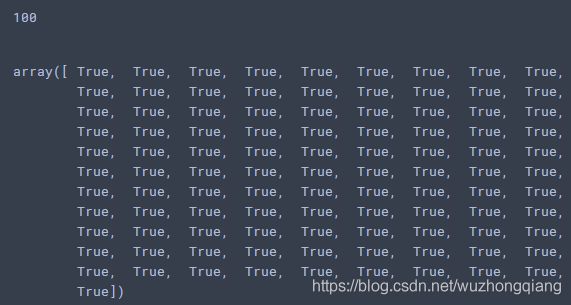
我们可以看一下网络玩的结果：

我们对比一下真实情况，看看网络错了多少：

print(np.sum(testY.max(1)[1].numpy() == np.array([fizz_buzz_encode(i) for i in range(1,101)])))
testY.max(1)[1].numpy() == np.array([fizz_buzz_encode(i) for i in range(1,101)])

我们可以发现，100个数，模型错了7个， 对了93个数，还算可以吧，毕竟只是单层的网络，你可以换成多层或者调调参数试试会不会好一些。（我加了一层60个单元的隐藏，然后特征长度改成了15，这样稍微简单一改，模型就到了100%的效果，并且只需要1000次迭代），你也可以试试其他的，既然有这么好的机会，好好利用，改改参数学习率啥的，换换优化方法啥的都可以

哈哈，是不是有种成就感呢？ 从没听过到Pytorch，到可以用Pytorch搭建神经网络并教他玩游戏，并且他也表现的不错，哈哈

6. 总结

好了，今天的内容到这里吧，稍微一下就10000多字，可能都没耐心看了吧， 但是上面的这个过程，如果深入进去，也是挺好玩的。 我还是简单总结一下吧：

首先，我们从Pytorch的理论出发，简单的介绍了理论知识，由于理论太多，没法面面俱到，只能点到为止，所以我们得擅长去查阅Pytorch手册，遇到不会的，及时查阅及时整理，才能把理论慢慢的学会了。

然后我们动手用numpy完成了两层的神经网络搭建，这个过程中，你亲自完成了前向传播，计算损失，反向传播，更新参数等操作，算是把神经网络这个黑盒子的过程打开了。 对神经网络的计算有种焕然一新的感觉。

然后，我们一步一步的从把numpy操作换成tensor操作开始，更换Pytorch的版本，接下来用autograd机制替代反向传播，用nn模型替代前向传播，用Pytorch的计算误差的方式和优化器替代计算损失和更新参数的部分，使得完成了一个Pytorch版本的两层神经网络，这个过程中，你亲身体会Pytorch的简洁和优秀。然后为了能搭建复杂的网络，我们写了一个类，继承了nn.modules模块，以后得熟悉这个写法。

最后，我们亲手搭建神经网络，并让他玩了一个小游戏，结果证明，他表现的还不错

一整套流程下来，希望有所收获吧，不管是知识上的还是乐趣上的都算，哈哈。 继续加油吧，我们进入Pytorch的下一篇，我们要学点高深的本领了，那么就从伟大的nlp开始吧，用Pytorch搭建语言模型。

如果对Keras也感兴趣，我现在正在写一个Keras的系列
这个更有趣，这个采用了将夜里面的升级方式，从感知开始，学习Keras的基础知识，学完之后就有了快速搭建神经网络的能力，然后升级进入Keras初识境，在这里面，会手把手用Keras搭建谷歌的Wide&Deep model(DNN)模型完成一个分类任务，搭建lenet5,alexnet,vgg16(CNN)玩转手写数字识别，搭建LSTM(RNN)进行唐诗的生成，搭建LSTM+attention完成机器翻译的小任务，搭建GAN(生成对抗网络)直接帮助我们生成手写数字或者其他类型的图片等，感知初步会有5篇文章，5个项目，这样下来，就能够用Keras把DNN，CNN，RNN，GAN等玩一个遍，这样就破镜了，进入不惑境界。 后面的故事还没有想好怎么进行，毕竟自己也在修炼中，用将夜里面的一句话来说，后面还是不可知之地，感知的部分也正在写，目前只完成了深度学习框架之Keras感知：你会快速搭建各种经典卷积神经网络(LeNet、AlexNet、VGG16)玩转手写数字识别吗？这一篇CNN。

总之，这是一个很有趣的修仙过程，哈哈，等着成仙吧