八种基本排序及其时间复杂度
排序的例子(步骤)是方便理解用的,与程序无关,程序自动生成n个随机数排序并输出运算时间,如想输出排序后的数,请自行更改
1.冒泡排序
将相邻的两个数两两比较,每次外循环都将最大的数移到最后,每次内循环比较两个数,如果后一个数小于前一个数,两个数交换。
15 6 34 22 8 12 30
6 15 22 8 12 30 34
6 15 8 12 22 30 34
6 15 8 12 22 30 34
6 8 12 15 22 30 34
6 8 12 15 22 30 34
6 8 12 15 22 30 34
#include
#include
#include
unsigned long long a[50000000];
double maopao(unsigned long long a[],int n)
{
int i,j,temp;
clock_t beg,end;//起始时间和结束时间
double time;
beg=clock();
for(i=0;i
{
for(j=1;j<=n-1-i;j++)
{
if(a[j]
{
temp=a[j];
a[j]=a[j-1];
a[j-1]=temp;
}
}
}
end=clock();
time=(double)(end-beg)/CLOCKS_PER_SEC;
return time; //运行时间
}
int main()
{
int n,i;
printf("请输入数字个数:");
scanf("%d",&n);
srand(time(NULL));
for(i=0;i
a[i]=rand();
}
printf("选择排序运行时间%f",maopao(a,n));
for(i=0;i
a[i]=i;
}
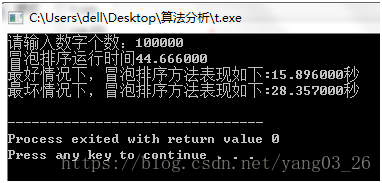
printf("最好情况下,冒泡排序方法表现如下:%f秒\n",maopao(a,n));
for(i=0;i
a[n-i-1]=i;
}
printf("最坏情况下,冒泡排序方法表现如下:%f秒\n",maopao(a,n));
return 0;
}
冒泡排序是最慢的排序算法,实际运用中效率最低,当数列为由小到大的有序数列时为最好情况,当由大到小时为为最坏情况。
2.选择排序
每进行一次外循环都找到一个最大的数移到后面,每次内循环将最大的数与数组中的某个数比较,如果最大值小于那个数,将那个数的下角标记录到max中。
15 6 34 22 8 12 30
15 6 30 22 8 12 34
15 6 12 22 8 30 34
15 6 12 8 22 30 34
8 6 12 15 22 30 34
8 6 12 15 22 30 34
6 8 12 15 22 30 34
#include
#include
#include
unsigned long long a[50000000];
double xuanze(unsigned long long a[],int n)
{
int max,i,j,temp;
clock_t beg,end;//起始时间和结束时间
double time;
beg=clock();
for(i=0;i
{
max=0;
for(j=1;j<=n-1-i;j++)
{
if(a[max]
{
max=j;
}
}
temp=a[max];
a[max]=a[n-1-i];
a[n-1-i]=temp;
}
end=clock();
time=(double)(end-beg)/CLOCKS_PER_SEC;
return time; //运行时间
}
int main()
{
int n,i;
printf("请输入数字个数:");
scanf("%d",&n);
srand(time(NULL));
for(i=0;i
a[i]=rand();
}
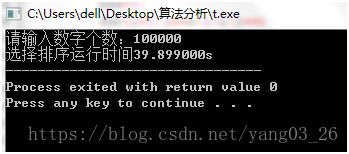
printf("选择排序运行时间%fs",xuanze(a,n));
return 0;
}
选择排序和冒泡排序差不多,使用较少
3.归并排序
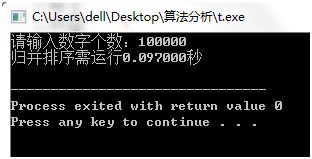
先将数组分成两份,再将两段分别进行归并排序后合到一起。
15 6 34 22 8 12 30
15 6 34 22| 8 12 30
15 6 | 34 22 | 8 12 | 30
15| 6 | 34| 22|8 |12| 30
6 15| 22 34 | 8 12| 30
6 15 22 34 |8 12 30
6 8 12 15 22 30 34
#include
#include
#include
unsigned long long a[50000000];
unsigned long long b[50000000];
void guibing(unsigned long longa[],unsigned long long b[],int i,int mid,int j)//将两段有序序列按从大到小合并
{
intm=i,n=mid+1,k=i,p;//m为头,n为后一段的第一个,k为数字存入b数组的位置
while(m!=mid+1&&n!=j+1)//当两端都未比较完时即都有剩余数时
{
if(a[m]>=a[n])//如果前段第一个数大于等于后一段第一个数
{
b[k]=a[m];//将后一段第一个数存入b数组中
m++;//后一段的第一个后移在进行比较
k++;
}
else
{
b[k]=a[n];//将前一段第一个数存入b中
n++;
k++;
}
}
while(m!=mid+1)//当二者有一个读取完,将剩下一个的有序数列直接存入b中
{
b[k]=a[m];//将后一段第一个数存入b数组中
k++;
m++;
}
while(n!=j+1)//当二者有一个读取完,将剩下一个的有序数列直接存入b中
{
b[k]=a[n];//将前一段第一个数存入b中
k++;
n++;
}
for(p=i;p<=j;p++)//将b给a
{
a[p]=b[p];
}
}
double fenduan(unsigned long longa[],unsigned long long b[],int i,int j)//将数据分段
{
intmid;
clock_t beg,end;//起始时间和结束时间
doubletime;
beg=clock();
if(i { mid=(i+j)/2;//分段的下角标 fenduan(a,b,i,mid);//前一段在调用本身函数进行分段直到首尾相等为止 fenduan(a,b,mid+1,j);//后一段在调用本身函数进行分段直到首尾相等为止 guibing(a,b,i,mid,j);//将排序后的有序数列归并 } end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; returntime; //归并函数运行时间 } int main() { intn,i; printf("请输入数字个数:"); scanf("%d",&n); srand(time(NULL)); for(i=0;i a[i]=rand(); } printf("归并排序需运行%f秒\n",fenduan(a,b,0,n));//随机序列 return0; } 归并排序不适合数据量较大的时候用,因为运用递归,数据量较大时,容易堆栈溢出错误。 4.基数排序 利用计数排序的原理,从最低位开始,进行按位的大小排序,直到最高位为止 #include #include #include unsigned long long a[50000000]; unsigned long long e[50000000]; unsigned long long b[50000000]; unsigned long long d[50000000]; void jishu(unsigned long long a[],unsignedlong long n) { unsignedlong long c[10],p=1,q=10; unsignedlong long i; for(i=1;i<=n;i++) { e[i]=a[i]; } while(p!=0) { for(i=0;i<=9;i++) { c[i]=0; } for(i=1;i<=n;i++) { b[i]=e[i]%10; } for(i=1;i<=n;i++) { c[b[i]]=c[b[i]]+1; } for(i=1;i<=9;i++) { c[i]=c[i]+c[i-1]; } for(i=n;i>=1;i--) { d[c[b[i]]]=a[i]; c[b[i]]=c[b[i]]-1; } for(i=1;i<=n;i++) { a[i]=d[i]; } p=0; for(i=1;i<=n;i++) { e[i]=a[i]; e[i]=e[i]/q; if(e[i]!=0) { p++; } } q=q*10; } } int main() { unsignedlong long n,i; printf("请输入数字个数(n<50000000):"); scanf("%d",&n); srand(time(NULL)); for(i=1;i<=n;i++){//随机生成待排数组0 a[i]=rand(); } clock_t beg,end;//起始时间和结束时间 doubletime; beg=clock(); jishu(a,n); end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; printf("随机生成数时基数排序运行时间:%f s\n",time); return0; } 基数排序(LSD)适用于位数较少的数列排序,如果位数较大,采用(MSD)方法,(MSD:与LDS相反从高位开始比较),适合用于字符串或整数。 5.计数排序 先将数组c赋值为0,依照c的下角标即为a数组中存的值,在c中依照下角标记录a数组中个数字出现的次数,再从第二个开始,将c中前一个数加到后一个数中,即为a数组中各数的地址,在按c数组的下角标来找a数组中数的真正地址来将数存入数组b中 8 10 4 2 9 6 3 C: 下角标0 1 2 3 4 5 6 7 8 9 10 值 0 0 1 1 1 0 1 0 1 1 1 C: 下角标0 1 2 3 4 5 6 7 8 9 10 地址 0 0 1 2 3 3 4 4 5 6 7 A: 值 8 10 4 2 9 6 3 地址5 7 4 1 6 4 2 #include #include #include #include unsigned long long a[50000000]; unsigned long long b[50000000]; unsigned long long c[50000000]; double js(unsigned long long a[],int n) { inti,max=a[1]; clock_t beg,end;//起始时间和结束时间 doubletime; beg=clock(); for(i=2;i<=n;i++) { if(max { max=a[i]; } } for(i=0;i<=max;i++) { c[i]=0; } for(i=1;i<=n;i++) { c[a[i]]=c[a[i]]+1; } for(i=1;i<=max;i++) { c[i]=c[i]+c[i-1]; } for(i=n;i>=1;i--) { b[c[a[i]]]=a[i]; c[a[i]]=c[a[i]]-1; } end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; return time; } int main() { intn,i,k; printf("请输入数字个数:"); scanf("%d",&n); srand(time(NULL)); for(i=1;i<=n;i++){//随机生成待排数组 a[i]=rand()%100; } printf("计数排序运行时间%fs",js(a,n)); return 0; } 计数排序是非比较排序,快于一切比较排序,计数排序适合范围比较小的数的排序,数的范围越大效率越低,是排1~100之间的数最好的排序方法。 6.快速排序 以标兵为轴,将数组分段,轴左边都比轴小,轴右边都比轴大,再将其两段分别进行快排,直到分段后最左边的数的下角标等于或大于最右边的数的下角标时停止。 15 6 34 22 8 12 30 12 6 8 | 15 | 22 34 30 8 6 |12| 15| 22| 34 30 6 8 12 15 22 34 30 #include #include #include unsigned long long a[100000000000]; void kuaipai(unsigned long longa[],unsigned long long m,unsigned long long r) { if(m { unsignedlong long i=m; unsignedlong long j=r; unsignedlong long temp; while(i { while(a[i] { j--; } if(i { temp=a[i]; a[i]=a[j]; a[j]=temp; i++; } while(a[i] { i++; } if(i { temp=a[i]; a[i]=a[j]; a[j]=temp; j--; } } if(i==j) { kuaipai(a,m,i-1); kuaipai(a,i+1,r); } } } int main() { unsignedlong long n,i; printf("请输入数字个数:"); scanf("%d",&n); srand(time(NULL)); for(i=1;i<=n;i++){//随机生成待排数组 a[i]=rand(); } clock_t beg,end;//起始时间和结束时间 doubletime; beg=clock(); kuaipai(a,1,n); end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; printf("一般情况快排运行时间:%f s\n",time); for(i=1;i<=n;i++){//随机生成待排数组 a[i]=i; } beg=clock(); kuaipai(a,1,n); end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; printf("最坏情况下快排运行时间:%f s\n",time); return0; } 快排比大部分算法都要快,除特殊情况下,一般情况下没有比它更快的,它不适用于数据量非常大时,容易发生堆栈溢出错误,当数列有大到小或由小到大时为最坏情况,选取的轴在最两侧。 7.随机化快速排序 在快排的基础上,每次快排之前,在数组中随意取一个数,将其与分段后数组中第一个数交换,在进行快排。 #include #include #include unsigned long long a[100000000000]; void suiji(unsigned long long a[],unsignedlong long m,unsigned long long r) { if(m { unsignedlong long temp=0,p; p=rand()%(r-m+1)+m; temp=a[m]; a[m]=a[p]; a[p]=temp; unsignedlong long i=m; unsignedlong long j=r; while(i { while(a[i] { j--; } if(i { temp=a[i]; a[i]=a[j]; a[j]=temp; i++; } while(a[i] { i++; } if(i { temp=a[i]; a[i]=a[j]; a[j]=temp; j--; } } if(i==j) { suiji(a,m,i-1); suiji(a,i+1,r); } } } int main() { unsignedlong long n,i; printf("请输入数字个数:"); scanf("%d",&n); srand(time(NULL)); for(i=1;i<=n;i++){//随机生成待排数组 a[i]=rand(); } clock_t beg,end;//起始时间和结束时间 doubletime; beg=clock(); suiji(a,1,n); end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; printf("随机产生成数时随机快排运行时间:%f s\n",time); return0; } 随机化快排相当于快排的优化,同快排一样,但消除了快排的最坏情况。 8.插入排序 从第二个数开始,与已排好的序列的最后一个数比较,如果其值小于最后一个数,则与前一个数比较,到找到小于它的数,将其插入到这个数的后面 15 6 34 22 8 12 30 15 6 15 6 15 34 6 15 22 34 6 8 15 22 34 6 8 12 15 22 34 6 8 15 22 30 34 #include #include #include unsigned long long a[100000000000]; double charu(unsigned long long a [],int n) { int i,j,key;//定义开始时间与结束时间 clock_tbeg,end;//起始时间和结束时间 double time; beg=clock(); for(i=1;i key=a[i]; j=i-1; while(j>=0&&a[j]>key){ a[j+1]=a[j]; a[j]=key; j--; } } end=clock(); time=(double)(end-beg)/CLOCKS_PER_SEC; return time; //运行时间 } int main() { int n; printf("请输入数字个数:"); scanf("%d",&n); int i,j; srand(time(NULL)); for(i=0;i a[i]=rand(); } printf("插入排序需运行%f秒\n",charu(a,n)); for(i=0;i a[i]=i; } printf("最好情况下,插入排序方法表现如下:%f秒\n",charu(a,n)); for(i=0;i a[n-i-1]=i; } printf("最坏情况下,插入排序方法表现如下:%f秒\n",charu(a,n)); return 0; } 插入排序不适合数据量比较大或重复次数较多的时候,当序列由小到大时为最好情况,当序列由大到小时情况最差。 时间复杂度(如有错误欢迎提出) 排序方法 平均情况 最坏情况 最好情况 稳定性 1.冒泡排序 N^2 N^2 n 稳定 2.选择排序 N N^2 N^2 不稳定 3.归并排序 nlogn nlogn nlogn 稳定 4.基数排序 Nlog(r)m Nlog(r)m Nlog(r)m 稳定 5.计数排序 N N N 稳定 6.快速排序 nlogn N^2 nlogn 不稳定 7.随机化快速排序 nlogn Nlogn Nlogn 不稳定 8.插入排序 N^2 N^2 nlogn 不稳定