2013 ACM/ICPC 南京网络赛 1002 - Parade Show
Parade Show
Problem Description

2013 is the 60 anniversary of Nanjing University of Science and Technology, and today happens to be the anniversary date. On this happy festival, school authority hopes that the new students to be trained for the parade show. You should plan a better solution to arrange the students by choosing some queues from them preparing the parade show. (one student only in one queue or not be chosen)
Every student has its own number, from 1 to n. (1<=n<=10^5), and they are standing from 1 to n in the increasing order the same with their number order. According to requirement of school authority, every queue is consisted of exactly m students. Because students who stand adjacent in training are assigned consecutive number, for better arrangement, you will choose in students with in consecutive numbers. When you choose these m students, you will rearrange their numbers from 1 to m, in the same order with their initial one.
If we divide our students’ heights into k (1<=k<=25) level, experience says that there will exist an best viewing module, represented by an array a[]. a[i] (1<=i<=m)stands for the student’s height with number i. In fact, inside a queue, for every number pair i, j (1<=i,j<=m), if the relative bigger or smaller or equal to relationship between the height of student number i and the height of student number j is the same with that between a[i] and a[j], then the queue is well designed. Given n students’ height array x[] (1<=x[i]<=k), and the best viewing module array a[], how many well designed queues can we make at most?
Input
Multiple cases, end with EOF.
First line, 3 integers, n (1<=n<=10^5) m (1<=m<=n) k(1<=k<=25),
Second line, n students’ height array x[] (1<=x[i]<=k,1<=i<=n);
Third line, m integers, best viewing module array a[] (1<=a[i]<=k,1<=i<=m);
First line, 3 integers, n (1<=n<=10^5) m (1<=m<=n) k(1<=k<=25),
Second line, n students’ height array x[] (1<=x[i]<=k,1<=i<=n);
Third line, m integers, best viewing module array a[] (1<=a[i]<=k,1<=i<=m);
Output
One integer, the maximal amount of well designed queues.
Sample Input
10 5 10 2 4 2 4 2 4 2 4 2 4 1 2 1 2 1
Sample Output
1
Source
2013 ACM/ICPC Asia Regional Nanjing Online
Recommend
liuyiding
-----------------KMP---------------
题目大意:
要从所给的长度为n的数字串A中,连续取出能够成为完美串的数字串,问最多有多少串 ?
如何称为完美串:给出一段长度为m的数字串B,他们的大小关系已确定,只要长度为n的数字串能够满足:
对于任意(i , j), 1<=i,j<=m ,若有 B[i]
k是指A数字串是从k+1开始取的 .
我们考虑两个数字串A,B
A[1],A[2],…,A[k]与B[1],B[2],…,B[k]匹配条件: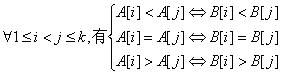
若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是: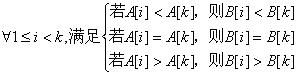
必须在与k无关的时间复杂度内完成该操作(在这里,A是模式串,B是原串)
然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作
(注意理解)
Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x
则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为:
接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK),具体实现时要注意Occur[p],Low[i],High[i]不存在的情况。
代码:
#include 
