浅谈求解最大流的方法
主要参考: 《算法导论》
引言
还是前几天参加的2014阿里巴巴春季校招(测试开发岗)笔试. 有道选择题:
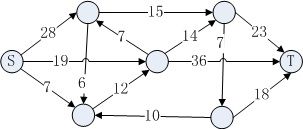
图1中标出了每条有向公路最大流量,请问从S到T最大流量是( ).
A.46 B. 47 C. 54 D.77
图1: 流网络
看到这一题的时候我非常懊悔, 因为最大流的算法记得看过, 却没复习到. 现在把它整理出来, 亡羊补牢.
接下来会先列出来相关的定义和定理. 精力有限, 只做罗列, 见谅!
然后给出这题的解题过程.
相关定义
流网络
流网络G=(V, E)是一个有向图, 图中每条边(u, v)∈E有一个非负的容量值c(u, v) ≥0. 并且对于(u, v)不存在反向边(v, u). 如果E中不存在(u, v), 则c(u, v)=0. 图1就是一个流网络.
流
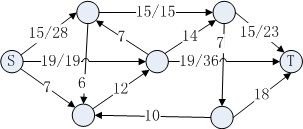
G中的流是一个实值函数f: V×V→R, 满足容量限制, 即f(u, v)≤c(u, v)和流量守恒性质, 即对于除S和T外的点满足流入与流出相等. 如图2所示.
图2: 流
残存网络
直观上说,给定G和f, 残存网络Gf就是由那些仍有空间对流量进行增加的边构成. 在流网络中, 若某条边的流量小于其容量, 则将其加入的Gf中; 若某条边流量等于其容量, 则这条边将不属于Gf
残存容量
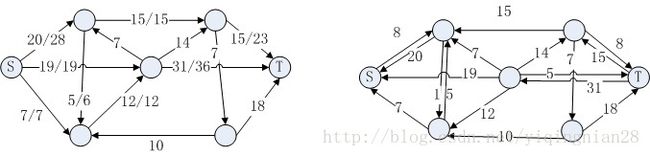
cf(u, v)的取值满足: 若(u, v)∈E, 则取c(u, v)-f(u, v)0; 若(v, u) ∈E, 则取f(v, u); 其他情况取0. 流和流对应的残存网络如图3所示.
图3: 流和流对应的残存网络
增广路径
增广路径p是残存网络Gf中一条从源节点S到汇点T的简单路径. 图4中加粗阴影所示的即是一条增广路径.
图4: 增广路径
最大流最小切割定理
设f是流网络G=(V, E)中的一个流, 源点为S, 汇点为T. 则下述条件是等价的:
(1) f是G的一个最大流.
(2) 残存网络Gf部包含任何增广路径.
(3) f的值等于G中某个切割的容量(本例中不涉及, 详情请自行百度).
Ford-Fulkerson算法
FORD_FULKERSON(G, s, t){
for each edge(u, v) ∈G.E
(u, v).f = 0
while Gf中存在一条s到t的增广路径p{
cf(p) = min{cf(u, v): (u, v) is in p}
for each edge(u, v) in p{
if (u, v)∈E {
(u, v).f += cf(p)
} else {
(v, u).f -= cf(p)
} } } }
Edmonds-Karp算法
查找增广路径可以用Edmonds-Karp算法选择从S到T的最短路径, 其中每条边的权重都为1. 也就是说以S为出发点广度优先遍历(BFS)图G, 到达T即终止.
解题过程
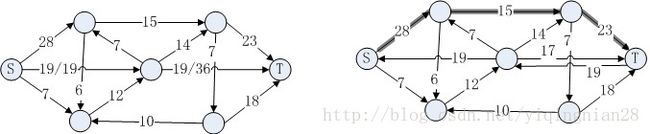
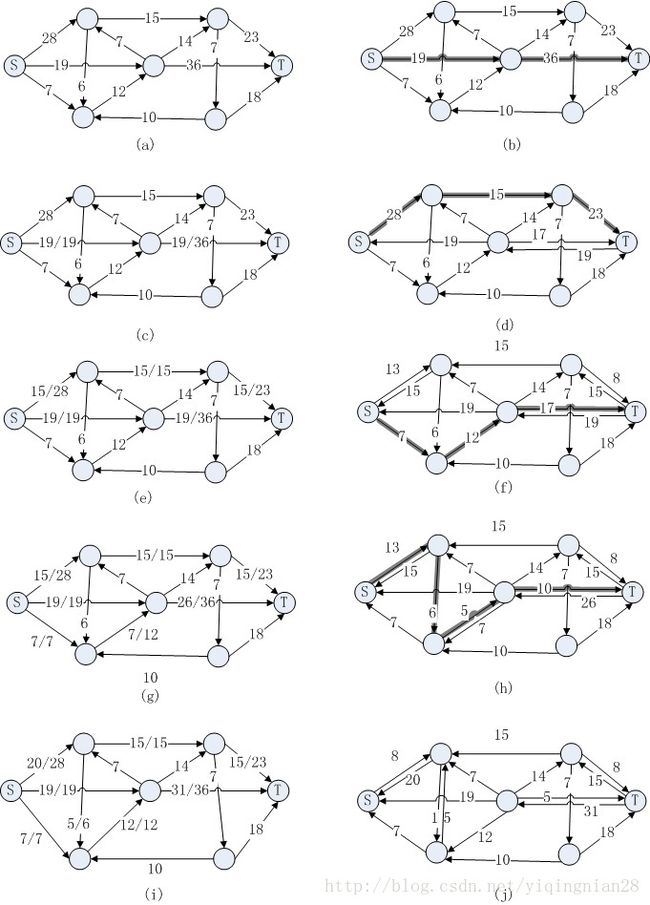
整个过程如图5所示. 图中边上的数字的含义是, f/c表示该边容量为c, 流量为f; 而单个数字c则表示容量为c, 流量为0.
图5 解题过程
图5中, 当到达(j)时已经找不到增广路径了, 则(i)中所示的流即为该流网络的最大流, 而流量则是流进T的流量总和, 即15+31=46. 故选A.
笔者水平有限, 上述过程难免会有错误, 如有发现, 还请指正!
转载请注明出处.