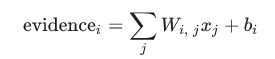人工智能实验四：深度学习算法及应用

一、实验目的

1、了解深度学习的基本原理；

2、能够使用深度学习开源工具识别图像中的数字；

3、了解图像识别的基本原理。

 

二、实验硬件软件平台

软件：操作系统：WINDOWS/Linux

应用软件：Tensorflow, PyTorch, Python，NumPy, SciPy, iPython

 

三、实验内容

安装开源深度学习工具设计并实现一个深度学习模型，它能够学习识别图像中的数字序列。然后使用数据训练它：你可以使用人工合成的数据（推荐），或直接使用现实数据。

 

源代码下载

链接：https://pan.baidu.com/s/1ud2EHK54X2KUpJsGZXS7Hg

密码：y7x1

 

本文参考资料

《深度学习之Tensorflow》

 

四、实验过程操作及现象

 

4.1 环境的搭建和配置

 

（1）本地搭建环境

 

使用实验指导书推荐环境，下载Anaconda3.4.1.1（注意版本号，官网可选，自带python3.5.4版本）

【请注意TensorFlow支持的python版本，我做实验那会它不支持python3.7，只支持老版本】

参考：https://blog.csdn.net/ITLearnHall/article/details/81708148

在命令行中执行：pip install --upgrade --ignore-installed tensorflow

即可下载安装TensorFlow到本地，如果安装的过程中提示要升级pip包，按照指令进行升级即可。

接下来是安装适应TensorFlow开发环境的python版本，因为tensorflow工具暂时还不支持最新的python3.7版本，在3.6环境下仍然有部分内容不兼容，但在3.5环境下是完美适配的。

执行以下指令：conda create --name tensorflow python=3.5，保证网络畅通即可安装完毕。

之后，执行指令activate tensorflow激活TensorFlow环境，接下来再往命令行输入spyder（Anaconda自带的python IDE），即可进入spyder界面输入python代码。

参考：https://blog.csdn.net/cs_hnu_scw/article/details/79695347

 

（2）服务器搭建环境（简单，推荐给有条件的同学）

 

使用Google colab所提供的免费服务器，注册Google账号，新建记事本输入python代码，并在菜单中的“代码执行程序”——“更改运行时刻类型”中选择python3和GPU加速，即完成了配置，需要注意的是这种方法需要科学上网（手动滑稽）。

 

4.2 各个算法的测试

 

在本次实验中，实现了两个算法，主要是两个部分，第一个部分是手写字体的数据集获取，这里我们使用了一个入门级别的计算机视觉库MINST，通过代码程序自动下载数据集到服务器存储，然后进行读取分析；第二部分是通过深度学习算法，使用训练集进行多轮次的迭代训练学习，通过训练集检测模型的准确性，输出识别数字的准确率。

 

（1）MINST数据集和数据的获取

 

MNIST是机器学习领域的一个经典问题，指的是让机器查看一系列大小为28x28像素的手写数字灰度图像，并判断这些图像代表0-9中的哪一个数字。每个数字由28*28的像素组成。

MINST包括三个数据集：训练集、测试集、验证集。data_sets.train是 55000个图像和标签（labels），作为主要训练集；data_sets.validation是5000个图像和标签，用于迭代验证训练准确度；data_sets.test 是10000个图像和标签，用于最终测试训练准确度（trained accuracy）。

在本次实验中，我们使用python代码下载MINST数据集，并保存在指定路径下：

//download.py
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

print ('MINST图像数据：',mnist.train.images)
print ('训练集规模：',mnist.train.images.shape)
print ('测试集规模：',mnist.test.images.shape)
print ('验证集规模：',mnist.validation.images.shape)

import pylab
print('数据集的第一张图片：')
im = mnist.train.images[0]
im = im.reshape(-1,28)
pylab.imshow(im)
pylab.show()

通过观察输出，我们了解了图像数据是一个28*28大小的图片和标签，其中28*28的矩阵表示的是图片数据，而标签则占用10位，我们可以将标签看作为一个数组，其中，正常情况下，数组中的每个元素都是0，只有当某一位为1的时候，它的下标，就是代表了图片中的数字，比如如果第一位为1（下标为0），且其他九位全部为0，那么，说明这张图片里面存放的手写数字是1。

据此分析，每个图片有且仅有一个标签与其对应，且每个标签中的10位，有且仅有一位是1，其余全部是零。

下图是以上代码的输出：

（2）基于softmax单层神经元的训练算法

 

下面，给出基于softmax分类单层神经元的训练算法的代码及其对应分析：（逐段分析讲解）

【这里为了解释清楚代码的每一段的作用，将代码拆分为很多个片段，如需要完整代码请去上面链接自取】

import tensorflow as tf #导入tensorflow库
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
import pylab

在第一部分阶段的时候，由于我们之前已经通过了代码下载好了MINST数据集，这里将其对应的文件位置作为路径，即可实现MINST数据集导入到算法中的操作，这里使用了一个input_data函数，有两个参数，第一个是数据集的路径，第二个是one_hot标记位。

这个one_hot标记位，表示将样本标签转化为one hot编码，这个编码的意思是：假如所有的编码一共有10类（0——9的10个数字），0的one hot就是1000000000，1的one hot就是0100000000，以此类推，属于哪一类，哪一位上就会变成1.

tf.reset_default_graph()
# tf Graph Input
x = tf.placeholder(tf.float32, [None, 784]) # mnist data维度 28*28=784
y = tf.placeholder(tf.float32, [None, 10])  # 0-9 数字=> 10 classes

这里声明了一个占位符（向量），None代表该向量的第一个维度是可以为任意长度的，因此，利用占位符X就能够保存所有任意数量的MINST图像（这里是55000张）；第二维度为784，即28的平方，代表每张图片所含有的784个像素点。

Y占位符则是保存每一张图片对应的标签，同样适用None匹配任意数量的数据集，且第二维度长度限定为10，代表与10个数字相对应。

# Set model weights
W = tf.Variable(tf.random_normal([784, 10]))
b = tf.Variable(tf.zeros([10]))

这里是定义学习参数。variable代表创建学习参数，用于之后的softmax模型构建，在这里，W使用了random函数，将参数设置为一个随机值，而b被设置为0。

# 构建模型
pred = tf.nn.softmax(tf.matmul(x, W) + b)   # Softmax分类

# Minimize error using cross entropy
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))

# 参数设置
learning_rate = 0.01
# 使用梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

首先，使用了tf，即TensorFlow库中的定义，使用matmul代表向量乘积运算，这里x和W都是二维张量，拥有多个输入，我们将它们相乘再加上b，把它们的和，输入到softmax函数中，这里也就是我们所说的正向传播过程。

接下来我们需要定义反向传播的过程，以下主要是由三部分构成的：

1、将生成的样本标签pred，与实际的样本标签y，做一次交叉熵的运算，取得平均值；

2、将这个结果作为一次正向传播的误差，通过梯度下降的方法找到这个能够使得误差最小化的b和W的偏移量；

3、更新b和W，使得其找到适合的参数。

整个这一部分的规则，主要就是要让误差值cost变小，这样才能让训练结果与标签数据越来越相近。其中，有一个学习率的定义，学习率代表每次迭代对于参数的调整幅度。

temp = input("请输入迭代次数：")
training_epochs = int(temp)
batch_size = 100
display_step = 100
saver = tf.train.Saver()
model_path = "lab4_model/operation190101_Tue_426d"

这里定义了几个全局变量。首先，程序提示用户输入次数，接下来，定义了size和step，size代表每次迭代取多少个数据训练；step代表迭代多少次输出一次准确率（迭代次数往往很多，频繁输出不仅会影响界面阅读效果，而且由于频繁的检查验证，会导致程序变慢），最后，定义了一个训练模型保存的地址。

# 启动session
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())# Initializing OP
    # 启动循环开始训练
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples/batch_size)
        # 遍历全部数据集
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs,y: batch_ys})
            # Compute average loss
            avg_cost += c / total_batch
        # 显示训练中的详细信息
        if (epoch+1) % display_step == 0:
            print ("第",'%d次迭代：'%(epoch+1),"cost=","{:.9f}".format(avg_cost))
    print("训练过程结束！")
    # 测试 model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # 计算准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print ("准确率：", round(accuracy.eval({x: mnist.test.images, y: mnist.test.labels})*100,2),"%")
    # Save model weights to disk
    save_path = saver.save(sess, model_path)
    print("模型已经保存，保存位置：%s" % save_path)

这里是一个正式训练的过程，每次训练取得MINST数据集中的100个数据进行训练，并实时检查交叉熵（cost）的值，运行的时候，我们会发现，交叉熵随着迭代次数的不断增长，会逐渐减小，说明训练的精确度也越来越高。

训练的过程分为两步：

1、训练，使用minst.train.next_batch函数，每次取得batch_size个元素进行训练；

2、计算交叉熵，使用的是sess.run([optimizer, cost], feed_dict={x: batch_xs,y: batch_ys})这个函数调用，且如果当前迭代次数能够整除display_step，就可以输出一次结果。

# 读取模型
print("\n读取模型，第二次测试")
with tf.Session() as sess:
    # Initialize variables
    sess.run(tf.global_variables_initializer())
    # Restore model weights from previously saved model
    saver.restore(sess, model_path)
    # 测试 model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # 计算准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print ("准确率：", round(accuracy.eval({x: mnist.test.images, y: mnist.test.labels})*100,2),"%")
    output = tf.argmax(pred, 1)
    batch_xs, batch_ys = mnist.train.next_batch(2)
    outputval,predv = sess.run([output,pred], feed_dict={x: batch_xs})
    print(outputval,predv,batch_ys)
    im = batch_xs[0]
    im = im.reshape(-1,28)
    pylab.imshow(im)
    pylab.show()
    im = batch_xs[1]
    im = im.reshape(-1,28)
    pylab.imshow(im)
    pylab.show()

这一步是对于首次训练模型的二次测试，经过第一次的训练，我们的模型已经在特定的位置被保存了下来，这一步从保存的位置再次读取模型，并使用测试集进行准确率的测试。

 

以上就是softmax神经元单层网络学习算法的主要思想和流程。

 

（3）基于CNN神经网络的学习算法

 

下面，给出基于CNN神经网络的训练算法的代码及其对应分析注释（拆分，逐句说明，需要完整代码请自取）：

该算法由于声明了函数，所以流程从主函数（最后）开始看！

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

tf.reset_default_graph()  #构建图表
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) #加载数据

#权重初始化函数
def weight_variable(shape): # 使用truncated_normal进行初始化
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

#偏置初始化函数
def bias_variable(shape): # 偏置定义为常量
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

def conv2d(x, W): #x是图片的所有参数，W是此卷积层的权重
 #卷积使用1步长（stride size），0边距（padding size）的模板，保证输出和输入是同一个大小
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#池化函数
def max_pool_2x2(x): 
  #池化的核函数大小为2x2，因此ksize=[1,2,2,1]，步长为2，因此strides=[1,2,2,1]
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],strides=[1, 2, 2, 1], padding='SAME')

def Bulit_CNN(x):

  with tf.name_scope('reshape'):
    x_image = tf.reshape(x, [-1, 28, 28, 1]) 

建立CNN网络的操作。首先，我们把x变成一个4d向量，其第2、第3维对应图片的宽、高，最后一维代表图片的颜色通道数。

 with tf.name_scope('conv1'): #第一层卷积层
    W_conv1 = weight_variable([5, 5, 1, 32])
    b_conv1 = bias_variable([32])
    h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) 

这里是第一层卷积，卷积核定义为5x5,1是输入的通道数目，32是输出的通道数目，每个输出通道对应一个偏置，经过卷积运算之后，并使用ReLu激活函数激活。

with tf.name_scope('pool1'): #第一层池化层
h_pool1 = max_pool_2x2(h_conv1) # pooling操作 

这里是第一层池化，什么是池化呢？我们本来的图片是28*28的，这里用到的是一个2*2的池化（函数定义在之前，这里我解释不清楚，直接说做了什么），通过了2*2的池化，等于将图片四等分，之后的图片规模变成了14*14。

with tf.name_scope('conv2'): #第二层卷积层
    W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64]) # 与输出通道一致
    h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)

这里是第二层卷积，卷积核还是5x5,32个输入通道，64个输出通道，与第一层卷积相同，卷积运算完毕之后，使用ReLu激活函数激活。更新神经元的权值。

with tf.name_scope('pool2'): #第二层池化层
    h_pool2 = max_pool_2x2(h_conv2) # pooling操作

这里是第二次池化操作。经过第二次2*2池化，图片缩减到7*7。

 with tf.name_scope('fc1'): 
  W_fc1 = weight_variable([7 * 7 * 64, 1024]) 
  b_fc1 = bias_variable([1024]) # 对应的偏置

    h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])  # 将最后操作的数据展开
    h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1) #把池化层输出的张量reshape成一些向量，乘上权重矩阵，加上偏置，然后对其使用ReLU

这里是全连接层，在这一步，图片尺寸减小到7x7，我们加入一个有1024个神经元的全连接层，用于处理整个图片，加上对应的偏置和展开数据，并最后再次使用relu激活函数。

    with tf.name_scope('dropout'): # 为了减少过拟合，我们在输出层之前加入dropout
    keep_prob = tf.placeholder(tf.float32)
    h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

为了防止过拟合，在全连接层和输出层之间定义了一个dropout，什么是dropout呢？通俗来说，就是让一定数目的神经元（百分比）没有输出，如果全部神经元都更改参数并有输出的话，很容易出现过拟合。

with tf.name_scope('fc2'): #输出
    W_fc2 = weight_variable([1024, 10]) # 最后一层权重初始化
    b_fc2 = bias_variable([10])  # 对应偏置

    y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2 
  return y_conv, keep_prob

输出层，返回CNN网络参数。

def CNN(y_conv, keep_prob,x,y_):
     with tf.name_scope('loss'):
          cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_,logits=y_conv) #返回交叉熵误差

     cross_entropy = tf.reduce_mean(cross_entropy) #求平均值

     with tf.name_scope('adam_optimizer'):
          train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)  # 调用梯度下降

     with tf.name_scope('accuracy'): #计算准确率
          correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
          correct_prediction = tf.cast(correct_prediction, tf.float32)

     accuracy = tf.reduce_mean(correct_prediction)

     with tf.Session() as sess:
          temp = input("请输入迭代次数：")
          sess.run(tf.initialize_all_variables())
          for i in range(int(temp)):
              batch = mnist.train.next_batch(100)  #使用SGD，每次选取100个数据训练
              if i % 100 == 0:
                  train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
                  print ("第"+str(i)+"次迭代，训练集正确率："+str(int(train_accuracy*100))+"%")
              train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
          #测试集正确率
          a = 200
          b = 50
          sum = 0
          for i in range(a):
              testSet = mnist.test.next_batch(b)
              c = accuracy.eval(feed_dict={x: testSet[0], y_: testSet[1], keep_prob: 1.0})
              sum += c * b
          print ("全体测试集正确率：" +str(round(sum/(b*a)*100,2))+"%")

这里是一个训练过程，我们主要需要注意的是，为了防止过拟合，在构建神经网络的时候定义了一个dropout，它的功能是让一定百分比的神经元没有输出。这里我们看到上面标出的两句话，第一句话用于检测模型的准确率，出于准确的考虑，dropout应该为1.0，即神经元都有输出，以能够得到近乎于正确的答案，但是在后一句话中，那是一个训练过程，训练不是测试，主要的任务并不是尽可能精确，而是防止过拟合，因此dropout定义为0.5，即50%的神经元没有输出。

x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
y_conv, keep_prob = Bulit_CNN(x)
CNN(y_conv, keep_prob,x,y_)

主函数部分，首先和softmax算法一样，定义了相同的占位符以读取MINST数据集，之后，我们将占位符X（全体MINST数据集）建立CNN网络，并返回网络相关参数y_conv, keep_prob，交给CNN函数做具体的训练操作。

 

五、算法原理

 

（1）softmax神经元分类

 

Softmax Regressions是一个非常经典的用于多分类模型的方法。就算是之后的笔记中讲到的更复杂的模型，他们的最后一层也是会调用Softmax 这个方法的。

一个Softmax Regressions主要有2步：
（1）分别将输入数据属于某个类别的证据相加
（2）将这个证据转换成概率

那么首先这个证据是个什么呢，其实就是一个线性模型，由权重w，与偏置项b组成：

i表示第i类，j表示输入的这张图片的第j个像素，也就是求将每个像素乘以它的权重w，在加上偏执项的和。

求出了evidence之后，就要使用softmax函数将它转换成概率了。

这里的softmax其实相当于是一个激活函数或者连接函数，将输出的结果转换成我们想要的那种形式（在这里，是转换成10各类别上的概率分布）。那么这个softmax的过程是经过了什么样的函数转换呢？如下公式：

展开以上公式：

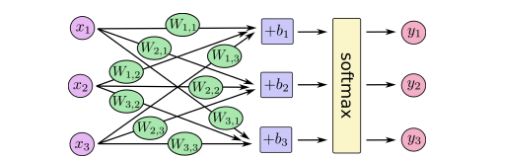
也就是说，将刚刚的线性输出evidence作为softmax函数里的输入x，先进过一个幂函数，然后做正态化，使得所有的概率相加等于1.将softmax regression的过程画出来如下：

如果写成公式，那就是如下：

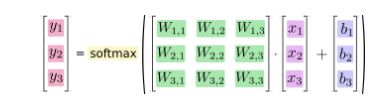
将以上公式做改进，变成矩阵和向量的形式：

要是想简单直观一点，那么就这样：

（2）CNN神经网络及其操作

 

1、CNN网络介绍

 

图像处理中，往往把图像表示为像素的向量，比如一个 1000×1000 的图像，可以表示为一个10^6 的向量，就如同在手写字神经网络中，输入层为28×28 = 784 维的向量。如果隐含层的节点个数与输入层一样，即也是10^6 时，那么输入层到隐含层的参数数据为 10^6×10^6 =10^12，参数的个数太多了，要想在正常的时间内训练完，基本是不可能的。所以要想处理1000×1000的图像分类，就得首先想办法减少参数的个数，也就是只基于深度神经网络（DNN）已经很难训练或者有没有更加优秀的算法可以专门处理这种图像分类呢？ 这就是卷积神经网络，convolutional neural network ，简称为 CNN 。

 

2、卷积操作

 

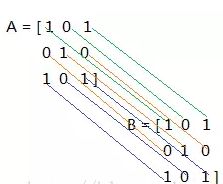
在卷积操作中，涉及到一种特殊的操作，叫做求内积，它是两个同型矩阵对应的元素相乘，然后求和。具体说来，如下：

A和B做内积后，得到一个数：1*1 + 0*0 + 1*1 + 0*0 + 1*1 + 0*0 + 1*1 + 0*0 + 1*1 = 5，这就是两个矩阵求内积得到的结果。

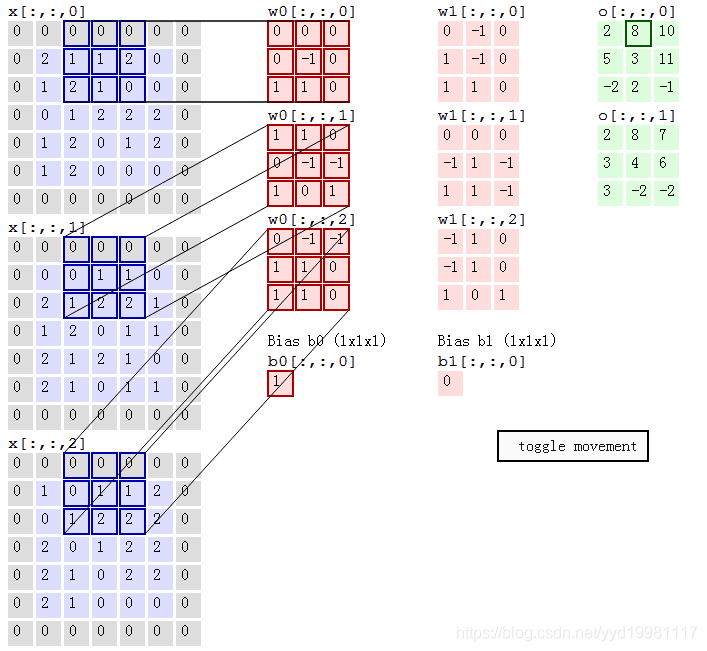
如果用多个卷积核进行卷积操作，应该是怎样的呢，为了表达方便，分享一个多核卷积操作的动画演示，图中的输入为 7 × 7 × 3，可以看到还做了一层零填充（Zero-padding），这是CNN中另一个重要的超参数，用到了两个过滤核：w0和w1，这在CNN中称为深度（Depth），是CNN三个超参数介绍的最后一个，分别用两个过滤核w0,和w1做了一次卷积操作，对应的得到两个卷积结果。

3、池化层（Pooling）

 

Pooling层能起到降低上一层输入的特征的维数的作用，但是同时能保持其最重要的信息，Pooling操作分多种：最大池化，平均池化，求和池化等。

以最大池化为例，池化一般在ReLU操作之后，首先定义一个相邻区域，然后求出这个区域的最大值，再选定一个步长，依次遍历完图像，如下图所示：

4、激活层

 

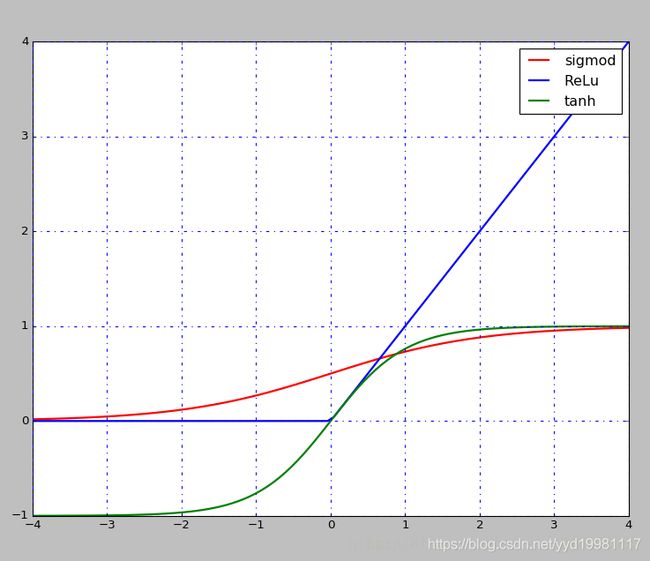
在每次卷积操作之后一般都会经过一个非线性层，也是激活层，现在一般选择是ReLu,层次越深，相对于其他的函数效果较好，还有Sigmod,tanh函数等。

5、Dropout层

 

dropout是一种防止模型过拟合的技术，这项技术也很简单，但是很实用。它的基本思想是在训练的时候随机的dropout(丢弃)一些神经元的激活，这样可以让模型更鲁棒，因为它不会太依赖某些局部的特征（因为局部特征有可能被丢弃）。

 

六、实验结果

左图为softmax神经元单层算法100次迭代；右图为CNN神经网络算法3000次迭代。在实验过程中，我进行过各种不同迭代次数的测试，这里测试100和3000次，因为写实验报告时的时间所限。

下表是两个算法之间的信息、性能比较：

	soft max单一神经元	CNN神经网络
准确率	1次迭代：35%左右 10次迭代：75%左右 100次迭代：87%左右	1次迭代：2%； 100次迭代：11%； 1000次迭代：95%； 3000次迭代：98%； 10000次迭代：99.2%左右；
运行速度	比较慢 只有单一神经元，就算打开GPU加速也无济于事，不适合迭代太多次数。	很快 网络层数多，开启GPU加速后并行性良好，迭代10000次，只需要2分钟左右。
算法优势	简单，易于实现； 训练周期短，且少量（不超过10次）的迭代就可以取得基本正确的效果（70%以上）	较为复杂，但是经过长期训练，迭代次数够多，准确率就能特别高。