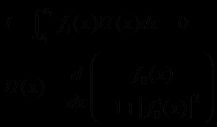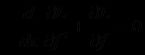欧拉-拉格朗日方程
欧拉-拉格朗日方程（The Euler-Lagrange equation）
最近经常看到这个，正好趁这次图像处理DDL总结一下。
文章结构
- 泛函
- 引例
- 欧拉拉格朗日方程
一、泛函
简单的说，泛函的定义域是函数集，值域是数集，也就是说，泛函是从函数空间到数域的一个映射。
实际上，推广开来，函数实际上是一种特殊的二元关系，二元关系是二阶笛卡尔积，所以函数集实际上是一个向量空间，所以泛函也可以说是从向量空间到标量的一个映射。
简而言之，泛函就是函数的函数。
泛函和函数的区别是：函数是变量和变量的关系，而泛函是变量和函数的关系。
二、引例
1.最短路径
众所周知，两点之间，线段最短。这是欧式几何的公理之一。从几何的角度很容易证明（反证）。但是，有没有解析的办法来证明呢？
答案是有的。
设平面上存在两点X1,X2，y=f(x)是平面上经过这两点的任意曲线。我们的目的，是求一个距离最短的f(x)，这是函数和数之间的二元关系。显然，这里的定义域是f(x)，也就是函数，而值域是距离，是一个数。所以这种关系是一个泛函，记为A[f]。
由弧微分公式易知
。
2.最速降线
最速降线问题是伽利略提出的著名问题：一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。换句话说，就是一个质点不是垂直的下落，只有重力做功，沿什么曲线下落所需时间最短。
这里的问题关键，是找到一条最优的曲线。下落时间是一个数值，所以这也是一个泛函问题。
由于只有重力做功，所以下落y之后的下落速度为
。
选取这条曲线上很小的一段，这一段中，速度可以看成不变。易知通过这一段的时间是
，分子是这一小段的弧长，分母是速度，所以这个值是通过这一段的时间。做一次积分，可以得到：
这就是总的时间，要求一个最优的f，使得该泛函的值最小。
三、欧拉-拉格朗日方程
这个方程是泛函中非常重要的方程，也是非常经典的能量泛函极小化的方法，不论在物理还是计算机领域，应用非常广泛。所谓能量泛函，是指微分的范数平方再积分。
它的最初的思想来源于微积分中“可导的极值点一定是稳定点（临界点）”。它的精髓思想在于：假定当前泛函的解已知，那么这个解必然使得泛函取得最小值（假定是最小值）。换言之，只要在泛函中加入任何扰动，都会使泛函的值变大，所以扰动为0的时候，就是泛函关于扰动的一个极小值。所以当扰动的能量趋近于0，泛函关于扰动的导数也是0。关键是扰动如何表示。答案是扰动用一个很小的数e乘上一个连续函数。当e趋近于0,意味着扰动也趋近于0。所以当a为0的时候，泛函对a的导数也为0。这就非常巧妙的把对函数求导的问题转化成了一个单因子变量求导的问题。这就是这个思想的伟大之处。
先不急于给出方程的具体形式，不妨根据上述思路，先用引例对方程做一个简单的推导（不是证明）。
函数f至少需为一阶可微的函数。若f0是一个局部最小值，而f1是一个在端点x1、x2取值为零并且至少有一阶导数的函数，则可得到以下的式子
其中ε为任意接近0的数字。
因此A[f0+εf1]对ε的导数(A的一阶导数)在ε=0时必为0。将A[f0+εf1]对ε求导，得到下式：
该式对于任意的满足条件的f1都成立。此条件可视为在可微分函数的空间中，A[f0]在各方向的导数均为0。若假设f0二阶可微，则利用分部积分法可得
其中f1为在两端点皆为0的任意二阶可微函数。记
其中f1为在两端点皆为0的任意可微函数。
若存在：使 H(x) > 0，即在周围有一区间内， H 为正值。
可以选择f1在此区间外为0，在此区间内为非负值，因此 I > 0，和前提不合。 若存在使H(x) < 0，也可证得类似的结果。因此可得到以下的结论：
由结论可推得下式：
这表明：两点间最短曲线为一直线。
一般地，考虑这样的泛函
形如这种形式的泛函，称为简单泛函。其中f二阶导连续。在这种情形下，满足欧拉-拉格朗日方程（简称E-L方程）：
比如上述的最短路径问题，直接带入E-L方程，可以得到同样的结论，此处不再赘述。
这里用E-L方程推导一下最速降线。
假定y二阶导连续，则它满足E-L方程：
因为
所以
带入F的表达式，得
化简得，
不妨设
带入上式，得
再对θ求导
即
两边对θ求积分
所以，得到的曲线是
这就是摆线方程。所以最速降线就是摆线。
（p.s. 最速降线也可以用微分方程的办法解）
参考资料：
1.泛函和变分法
https://wenku.baidu.com/view/de17ef3a5727a5e9856a6164.html
2.变分法与最速降线的证明
http://www.docin.com/p-23966935.html
3.欧拉-拉格朗日方程的三种推导
https://wenku.baidu.com/view/0db3984cc281e53a5902ff31.html