单调栈应用总结
栈基本概念:https://blog.csdn.net/qq_19446965/article/details/102982047
单调栈
- 单调递减栈:数据出栈的序列为单调递减序列
- 单调递增栈:数据出栈的序列为单调递增序列
单调栈模板:
for (遍历这个数组)
if (栈空 || 栈顶元素>=或者<=当前比较元素):
入栈
else:
while (栈不为空 && 栈顶元素<或者>当前元素)
栈顶元素出栈;
更新结果;
当前数据入栈;
1、单调递减栈
题目:每日温度
根据每日 气温 列表,请重新生成一个列表,对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/daily-temperatures/
def dailyTemperatures(self, T: List[int]) -> List[int]:
res_list = [0]*len(T)
stack = []
for i in range(len(T)):
while stack and T[i] > T[stack[-1]]:
res_list[stack[-1]] = i - stack[-1]
stack.pop()
stack.append(i)
return res_list2、单调递增栈
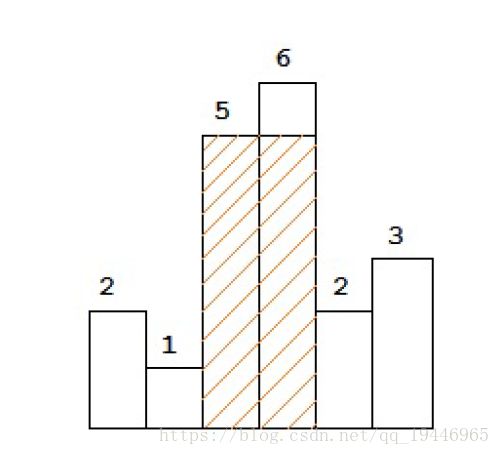
题目:柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
如上图所示,从左到右处理直方,当 i=4 时,小于当前栈顶(即直方3),对于直方3,无论后面还是前面
的直方,都不可能得到比目前栈顶元素更高的高度了,处理掉直方3(计算从直方3到直方4之间的矩形的面
积,然后从栈里弹出);对于直方2也是如此;直到碰到比直方4更矮的直方1。
这就意味着,可以维护一个递增的栈,每次比较栈顶与当前元素。如果当前元素大于栈顶元素,则入栈,
否则合并现有栈,直至栈顶元素小于当前元素。结尾时入栈元素0,重复合并一次。
def largestRectangleArea(self, heights):
heights = [0] + heights + [0] # 添加左右两侧的特殊边界使得只有一个柱子时,也可以形成一个倒V型
lens = len(heights)
max_high = heights[0]
stack = []
for i in range(lens):
while stack and heights[i] < heights[stack[-1]]:
peek = stack.pop()
max_high = max((i - stack[-1] - 1) * heights[peek], max_high) # 对于stack[-1]来说其right_i=i,left_i=stack[-2]
stack.append(i)
return max_high本题其余扩展参考另一篇文章:https://mp.csdn.net/console/editor/html/82048028
3、单调栈+前缀和
题目1:和至少为 K 的最短子数组
返回 A 的最短的非空连续子数组的长度,该子数组的和至少为 K 。
如果没有和至少为 K 的非空子数组,返回 -1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shortest-subarray-with-sum-at-least-k/
前缀和参考:https://blog.csdn.net/qq_19446965/article/details/104723466
其实这道题的方法是优先队列,和单调栈区别就是pop元素的位置是从list首。
关于单调队列:
- 单调队列的队首元素一定是最值元素;
- 单调队列队尾进元素时和单调栈一样,对于破坏单调性的元素直接弹出队尾,
- 这样就能保证对于单调队列中的每个元素,其前面的相邻元素一定是原数组向左第一个大于或小于当前元素的值;
- 队列中最后都有那些值取决于队尾进的是谁;
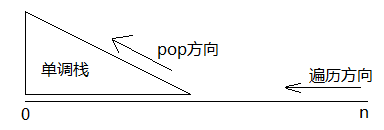
因为求最大值时候的遍历方向和pop方向:
def shortestSubarray(self, A, K):
N = len(A)
B = [0] * (N + 1)
for i in range(N): B[i + 1] = B[i] + A[i] # 求前缀和
d = collections.deque() # 优先队列
res = N + 1
for i in range(N + 1):
while d and B[i] - B[d[0]] >= K:
res = min(res, i - d.popleft())
while d and B[i] <= B[d[-1]]:
d.pop()
d.append(i)
return res if res <= N else -1
题目2:表现良好的最长时间段
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-well-performing-interval/
因为求最大值时候的遍历方向和pop方向:
def longestWPI(self, hours):
# 转换数组为1或-1
new_hours =[]
for h in hours:
if h > 8:
new_hours.append(1)
else:
new_hours.append(-1)
# 求前缀和
sums = [0]
for i in range(len(hours)):
sums.append(sums[-1] + new_hours[i])
# 建立单调递增栈
stack = []
n = len(sums)
for i in range(n):
if not stack or sums[stack[-1]] > sums[i]:
stack.append(i)
# 遍历求最大值
res = 0
for i in range(n-1, -1, -1):
while stack and sums[i] > sums[stack[-1]]:
res = max(res, i - stack[-1])
stack.pop()
return res总结:
通过题目1和题目2可以看出:
- 梯度递增方向要和遍历方向相同
- 求最大值时候,单调递减,要从n-0,同时遍历递减序列
- 求最小值时候,单调递增,要从0-n,同时遍历递增序列
其余栈的应用:
栈基本概念:https://blog.csdn.net/qq_19446965/article/details/102982047
接雨水:https://blog.csdn.net/qq_19446965/article/details/104144187
矩阵中最大矩形:https://blog.csdn.net/qq_19446965/article/details/82048028
基本计算器类:https://blog.csdn.net/qq_19446965/article/details/104717537
单调栈的应用:https://blog.csdn.net/qq_19446965/article/details/104720836