Andres_Lionel
Andres_Lionel

Flower【HDU-6849】【动态点分治+树状数组】

2020 Multi-University Training Contest 7 F题

  有一个N个点的树，给予其中M个操作，每次选其中一个点x，{x, r, v}，给它一个影响范围为r的权值为v的值，我们现在想要选取最多的权值点，使得两两之间是没有可重叠区间的。

  这个问题画在一维平面上其实很好做，也就是对于一段排序，然后维护的就是一个线段树优化dp，当我们选取这个点pos的时候，我们只能选择dp[1 \rightarrow pos - r - 1]的点，或者说，我们假设在[(pos - r) \rightarrow (pos + r) ]中，如果选择其他的更优，那么，我们可以不将这个点加进我们所选的集合中去。

  于是，可以讲这个操作转换为，我们先将影响深度深的点给放进去，然后按照上面的类似贪心方法进行判断。

  如果我们取这个点，比之前选取的点更优的话，我们可以选择这个点代替和它冲突的点，当然，还是可以继承和它不冲突的点的，于是，我们首先对影响区间最深的点开始这样的操作，这样的目的是为了我们其实只用考虑一个端点，而且用一个类似于差分的思想，我们可以判断取这个点是否更优。

画图说明：

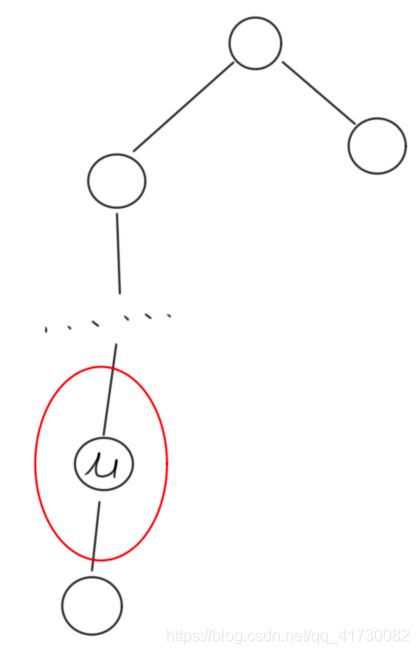
Flower【HDU-6849】【动态点分治+树状数组】_第1张图片

  如果存在这样一个点u，我们设它的深度为deep[u]，然后对于u点假如存在一个影响的范围r，可以知道它最向上影响的深度为deep[u] - r的点，我们根据这个信息，来对所有的点进行{\color{Red} deep[u] - r}降序排序，于是，可以考虑之后放入的点v，如果被之前覆盖的点能够影响到的话，也就是对应它的向上r步的点（深度为deep[u] - r，或者当deep[u] - r为小于等于0时就是原树根节点），在点v的范围内，所以，我们将u的贡献点放在它向上r步的点，然后把它产生的贡献放在该点上。

  然后，现在就是查询有多少的冲突贡献，我们可以算它覆盖范围内的点的权值和即可，当然，这里的“点”指的是原点向上r步的点。

  贡献：假设冲突的点产生的总贡献为sum，那么这个点如果要取的话（如果它本身的价值还不足sum的话，要它何用？），那么它产生的贡献为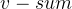v - sum。所以，对于放进去的第一个点，它的贡献就是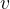v，因为在它之前就没有任何贡献了，所以根据这样的信息，我们可以维护出来所有点的关系，又因为它是根据“向上r步”的点来进行操作的，所以保证了影响点的深度一定是上升的，所以不存在先取之前的，而跳过中间的点的这样的情况。

操作实现

  现在问题转化了，变成了求它的r步范围内的“权值点”的权值之和，那样，我们可以用动态点分治来实现，因为按照类似时间戳这样的方式进行插入，所以不可永久化，我们用一个数据结构维护这个关系即可（自然选用简单的树状数组啦！）。

  所以，就是一个差分的关系了，我们找到这个点，然后不断的向它的点分治父亲节点走，每次算向周围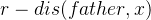r - dis(father, x)距离的点的权值和，当然，这样就很容易把自己方向的点给多算了，所以点分治的时候记录在自己方向上的father的下一个点即可。

Code

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 1e5 + 7;
int N, Q;
namespace Graph
{
    int head[maxN], cnt;
    struct Eddge
    {
        int nex, to;
        Eddge(int a=-1, int b=0):nex(a), to(b) {}
    } edge[maxN << 1];
    inline void addEddge(int u, int v)
    {
        edge[cnt] = Eddge(head[u], v);
        head[u] = cnt++;
    }
    inline void _add(int u, int v) { addEddge(u, v); addEddge(v, u); }
    inline void init()
    {
        cnt = 0;
        for(int i=1; i<=N; i++) head[i] = -1;
    }
};
using namespace Graph;
namespace Segement
{
    vector tr[20][maxN];
    void Clear()
    {
        for(int i=0; i<20; i++)
        {
            for(int j=1; j<=N; j++)
            {
                tr[i][j].clear();
            }
        }
    }
    inline ll query(vector &vt, int x)  //x == distance + 1 in order to solve f(x == 0)
    {
        ll ans = 0;
        while(x)
        {
            ans += vt[x];
            x -= lowbit(x);
        }
        return ans;
    }
    inline void update(vector &vt, int x, ll val)
    {
        int _UP = (int)vt.size() - 1;
        while(x <= _UP)
        {
            vt[x] += val;
            x += lowbit(x);
        }
    }
};
using namespace Segement;
namespace Divide
{
    int vis[maxN];
    int maxx, root, all, fa[maxN], siz[maxN], son[maxN], dis_from_ff[maxN][20], under_ff[maxN][20];
    void Init()
    {
        for(int i=1; i<=N; i++) vis[i] = 0;
        maxx = INF;
    }
    void find_root(int u, int fa)
    {
        siz[u] = 1; son[u] = 0;
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(vis[v] || v == fa) continue;
            find_root(v, u);
            siz[u] += siz[v];
            son[u] = max(son[u], siz[v]);
        }
        son[u] = max(son[u], all - siz[u]);
        if(son[u] < maxx)
        {
            maxx = son[u];
            root = u;
        }
    }
    void dfs(int u, int father, int depth)
    {
        siz[u] = 1;
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(vis[v] || v == father) continue;
            dis_from_ff[v][depth] = dis_from_ff[u][depth] + 1;
            under_ff[v][depth] = under_ff[u][depth];
            dfs(v, u, depth);
            siz[u] += siz[v];
        }
    }
    void node_Divide(int u, int depth)
    {
        vis[u] = depth;
        tr[depth][u].resize(all + 2);
        int tot_siz = all;
        dis_from_ff[u][depth] = 0;
        for(int i=head[u], v, tmp_siz; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(vis[v]) continue;
            dis_from_ff[v][depth] = dis_from_ff[u][depth] + 1;
            under_ff[v][depth] = v;
            tmp_siz = siz[u] > siz[v] ? siz[v] : all - siz[u];
            tr[depth][v].resize(tmp_siz + 2);
            dfs(v, u, depth);
        }
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(vis[v]) continue;
            all = siz[u] > siz[v] ? siz[v] : tot_siz - siz[u];
            maxx = INF;
            find_root(v, u);
            fa[root] = u;
            dis_from_ff[root][depth + 1] = 0;
            under_ff[root][depth + 1] = root;
            node_Divide(root, depth + 1);
        }
    }
};
using namespace Divide;
int deep[maxN], lca_fa[maxN][20];
void dfs_Deep(int u, int father)
{
    deep[u] = deep[father] + 1; lca_fa[u][0] = father;
    for(int i=head[u], v; ~i; i=edge[i].nex)
    {
        v = edge[i].to;
        if(v == father) continue;
        dfs_Deep(v, u);
    }
}
struct Question
{
    int x, r, v;
    Question(int a=0, int b=0, int c=0):x(a), r(b), v(c) {}
    inline void In() { scanf("%d%d%d", &x, &r, &v); }
    friend bool operator < (Question e1, Question e2) { return deep[e1.x] - e1.r > deep[e2.x] - e2.r; }
} ques[maxN];
inline ll ask(int x, int r)
{
    ll sum = 0;
    int depth = vis[x];
    sum = query(tr[depth][x], min(r + 1, (int)tr[depth][x].size() - 1));
    int y = fa[x];
    while(y)
    {
        depth--;
        if(dis_from_ff[x][depth] <= r)
        {
            sum += query(tr[depth][y], min(r + 1 - dis_from_ff[x][depth], (int)tr[depth][y].size() - 1));
            sum -= query(tr[depth][under_ff[x][depth]], min(r + 1 - dis_from_ff[x][depth], (int)tr[depth][under_ff[x][depth]].size() - 1));
        }
        y = fa[y];
    }
    return sum;
}
inline void push_into(int x, ll val)
{
    int depth = vis[x];
    update(tr[depth][x], 1, val);
    int y = fa[x];
    while(y)
    {
        depth--;
        update(tr[depth][y], dis_from_ff[x][depth] + 1, val);
        update(tr[depth][under_ff[x][depth]], dis_from_ff[x][depth] + 1, val);
        y = fa[y];
    }
}
int main()
{
    int T; scanf("%d", &T);
    while(T--)
    {
        scanf("%d%d", &N, &Q);
        Graph::init();
        Divide::Init();
        Segement::Clear();
        for(int i=1, u, v; i= now.v) continue;
            ans += now.v - sum;
            x = now.x;
            for(int j=19; j>=0; j--) if((now.r >> j) & 1) x = lca_fa[x][j];
            if(!x) x = 1;
            push_into(x, now.v - sum);
        }
        printf("%lld\n", ans);
    }
    return 0;
}

 

你可能感兴趣的:(动态点分治,点分治,数据结构,动态点分治,树状数组)

  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
    1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • 数据结构之哈希表 X同学的开始 数据结构数据结构散列表
    哈希表(散列表)出现的原因在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • 4.C_数据结构_队列 荣世蓥 数据结构数据结构
    概述什么是队列：队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词：队尾：写入数据的一段队头：读取数据的一段空队：队列中没有数据，队头指针=队尾指针满队：队列中存满了数据，队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下：typedefintdata_t;//队列数据类型#defineN64//队列容量typ
  • C++八股 Petrichorzncu 八股总结c++开发语言
    这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
  • 【树一线性代数】005入门 Owlet_woodBird 算法
    Index本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数，采用顺序存储方式保存，数据结构定义如下:t
  • python获取子进程返回值_Python对进程Multiprocessing子进程返回值 weixin_39752157 python获取子进程返回值
    在实际使用多进程的时候，可能需要获取到子进程运行的返回值。如果只是用来存储，则可以将返回值保存到一个数据结构中；如果需要判断此返回值，从而决定是否继续执行所有子进程，则会相对比较复杂。另外在Multiprocessing中，可以利用Process与Pool创建子进程，这两种用法在获取子进程返回值上的写法上也不相同。这篇中，我们直接上代码，分析多进程中获取子进程返回值的不同用法，以及优缺点。初级用法
  • 【数据结构-一维差分】力扣2848. 与车相交的点 hlc@ 数据结构数据结构leetcode算法
    给你一个下标从0开始的二维整数数组nums表示汽车停放在数轴上的坐标。对于任意下标i，nums[i]=[starti,endi]，其中starti是第i辆车的起点，endi是第i辆车的终点。返回数轴上被车任意部分覆盖的整数点的数目。示例1：输入：nums=[[3,6],[1,5],[4,7]]输出：7解释：从1到7的所有点都至少与一辆车相交，因此答案为7。示例2：输入：nums=[[1,3],[5
  • JavaScript `Map` 和 `WeakMap`详细解释 跳房子的前端 JavaScript原生方法javascript前端开发语言
    在JavaScript中，Map和WeakMap都是用于存储键值对的数据结构，但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序，并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对：set(key,value):将一个键值对添加到Map中。如果键已经存在，则更新其对应的值。get(key):获取指定键的值。如果键
  • 【高阶数据结构】并查集 椿融雪 数据结构与算法数据结构并查集
    文章目录一、并查集原理二、并查集实现三、并查集应用一、并查集原理在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，
  • python中文版软件下载-Python中文版 编程大乐趣
    python中文版是一种面向对象的解释型计算机程序设计语言。python中文版官网面向对象编程，拥有高效的高级数据结构和简单而有效的方法，其优雅的语法、动态类型、以及天然的解释能力，让它成为理想的语言。软件功能强大，简单易学，可以帮助用户快速编写代码，而且代码运行速度非常快，几乎可以支持所有的操作系统，实用性真的超高的。python中文版软件介绍：python中文版的解释器及其扩展标准库的源码和编
  • 开发游戏的学习规划 杰克逊的日记 游戏学习
    第一阶段：●C#语言快速系统地学习一遍（基础的语法、面向对象、基础的数据结构、基础的设计模式）●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验：需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例，将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法，并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
  • 六、全局锁和表锁：给表加个字段怎么有这么多阻碍 nieniemin
    数据库锁设计的初衷是处理并发问题。作为多用户共享的资源，当出现并发访问的时候，数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。根据加锁的范围，MySQL里面的锁大致可以分成全局锁、表级锁和行锁三类。6.1全局锁全局锁就是对整个数据库实例加锁。MySQL提供了一个加全局读锁的方法，命令是Flushtableswithreadlock(FTWRL)。当你需要让整个库处于
  • Golang Channel PandaSkr golang
    Channel解析1.Channel源码分析1.1Channel数据结构typehchanstruct{qcountuint//channel的元素数量dataqsizuint//channel循环队列长度bufunsafe.Pointer//指向循环队列的指针elemsizeuint16//元素大小closeduint32//channel是否关闭0-未关闭elemtype*_type//元素类
  • ⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表 英雄哪里出来 《LeetCode算法全集》算法数据结构链表c++归并排序
    饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述  将两个不降序链表合并为一个新的不降
  • 数据结构 1 五花肉村长 数据结构算法开发语言c语言visualstudio
    1.什么是数据结构数据结构（DataStructure）是计算机存储和组织数据的方式，是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法（Algorithm）就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识，可以去看《剑指offer》和《
  • 【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】 NeVeRMoRE_2024 数据结构与算法实践数据结构算法leetcodeb树
    数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入：root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出：[[5,4,11,2],[
  • 【Python】数据结构,链表,算法详解 AIAdvocate python数据结构链表排序算法广度优先深度优先
    今日内容大纲介绍自定义代码-模拟链表删除节点查找节点算法入门-排序类的冒泡排序选择排序插入排序快速排序算法入门-查找类的二分查找-递归版二分查找-非递归版分线性结构-树介绍基本概述特点和分类自定义代码-模拟二叉树1.自定义代码-模拟链表完整版"""案例:自定义代码,模拟链表.​背景: 顺序表在存储数据的时候,需要使用到连续的空间,如果空间不够,就会导致扩容失败,针对于这种情况,我们可以通过链表实现
  • AI教你学Python 第4天：函数和模块 凡人的AI工具箱 AI教你学Pythonpython开发语言人工智能AIGC
    第四天：数据结构一、什么是数据结构？数据结构是计算机科学中用于组织和存储数据的特定方式。良好的数据结构能够提高数据的访问效率、修改频率和管理能力。Python提供了多种内置数据结构，如列表、元组、字典和集合，便于开发者更有效地处理数据。二、Python中的基本数据结构1.列表（List）定义：列表是一个有序的可变集合，允许重复元素。使用方括号[]表示。#示例：定义一个列表fruits=['appl
  • 互联网 Java 工程师面试题（Java 面试题四） 苹果酱0567 面试题汇总与解析java中间件开发语言springboot后端
    下面列出这份Java面试问题列表包含的主题多线程，并发及线程基础数据类型转换的基本原则垃圾回收（GC）Java集合框架数组字符串GOF设计模式SOLID抽象类与接口Java基础，如equals和hashcode泛型与枚举JavaIO与NIO常用网络协议Java中的数据结构和算法正则表达式JVM底层Java最佳实JDBCDate,Time与CalendarJava处理XMLJUnit编程现在是时候给
  • C# Tuple、ValueTuple 語衣 C#知识补充c#
    栏目总目录TupleTuple是C#4.0引入的一个新特性，主要用于存储一个固定数量的元素序列，且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构，非常适合用于临时存储数据，而无需定义完整的类或结构体。优点简便性：可以快速创建一个包含多个不同类型数据的对象，而无需定义新的类或结构体。灵活性：元素数量和类型在编译时确定，但可以在不同上下文中重复使用不同元素的Tuple。缺点性能：作为引用
  • Rust中的所有权和借用规则详解 代码云1 rust开发语言后端
    Rust是一种系统编程语言，其设计目标包括内存安全、并发安全以及性能。为了实现这些目标，Rust引入了一系列独特的编程概念，其中最为核心的就是所有权（Ownership）和借用（Borrowing）规则。本文将详细解释Rust中的所有权和借用规则，以及它们如何确保内存安全和并发安全。一、所有权规则在Rust中，每一个值都有一个与之关联的所有者。这个所有者可以是变量、数据结构或者是其他形式的存储。所
  • 二叉树--python 电子海鸥 Python数据结构与算法python开发语言数据结构
    二叉树一、概述1、介绍是一种非线性数据结构，将数据一分为二，代表根与叶的派生关系，和链表的结构类似，二叉树的基本单元是结点，每个节点包括值和左右子节点引用。每个节点都有两个引用（类似于双向链表），分别指向左子节点和右子节点，该节点被称为这两个子节点的父节点。当给定一个二叉树的结点时，我们将在该节点的左子节点以及其以下结点所形成的树称为左子树，同理，右子节点的部分被称为右子树。在二叉树中，除了叶节点
  • 使用WAF防御网络上的隐蔽威胁之反序列化攻击 baiolkdnhjaio 网络安全
    什么是反序列化反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串（如JSON、XML），它是对象序列化（即对象转换为可存储或可传输格式）的逆过程。反序列化的安全风险反序列化的安全风险主要来自于处理不受信任的数据源时的不当反序列化。如果应用程序反序列化了恶意构造的数据，攻击者可能能够执行代码、访问敏感数据、进行拒绝服务攻击等。这是因为反序列化过程中可能会自动触
  • java 线程池 队列封装_java线程池（线程池组---分离任务队列和线程池） 爱打怪的小魔女 java线程池队列封装
    线程池本质上所使用的逻辑模型仍然是我们熟悉的“生产者/消费者”模型。生产消费外部线程(生产者)－－－>任务消费者和生产者共享一个数据结构(缓存任务)PriorityQueue；生产者将任务添加到队列中，消费者从队列中取出数据；队列和线程池(线程池内部维护一个线程数组)，完全耦合在一起，当任务特别多，队列就不断的膨胀，增多，拥堵；就向车子过洞子另外一头走不掉，我靠，长龙(世界最长堵车世界纪录在天朝2
  • jquery实现的jsonp掉java后台 知了ing javajsonpjquery
    什么是JSONP？ 先说说JSONP是怎么产生的： 其实网上关于JSONP的讲解有很多，但却千篇一律，而且云里雾里，对于很多刚接触的人来讲理解起来有些困难，小可不才，试着用自己的方式来阐释一下这个问题，看看是否有帮助。 1、一个众所周知的问题，Ajax直接请求普通文件存在跨域无权限访问的问题，甭管你是静态页面、动态网页、web服务、WCF，只要是跨域请求，一律不准； 2、
  • Struts2学习笔记 caoyong struts2
    SSH : Spring + Struts2 + Hibernate 三层架构(表示层,业务逻辑层,数据访问层) MVC模式 (Model View Controller) 分层原则:单向依赖，接口耦合 1、Struts2  =  Struts  + Webwork 2、搭建struts2开发环境    a>、到www.apac
  • SpringMVC学习之后台往前台传值方法 满城风雨近重阳 springMVC
    springMVC控制器往前台传值的方法有以下几种： 1.ModelAndView    通过往ModelAndView中存放viewName：目标地址和attribute参数来实现传参：      ModelAndView mv=new ModelAndView();  mv.setViewName="success
  • WebService存在的必要性？ 一炮送你回车库 webservice
    做Java的经常在选择Webservice框架上徘徊很久，Axis  Xfire Axis2 CXF ，他们只有一个功能，发布HTTP服务然后用XML做数据传输。 是的，他们就做了两个功能，发布一个http服务让客户端或者浏览器连接，接收xml参数并发送xml结果。 当在不同的平台间传输数据时，就需要一个都能解析的数据格式。 但是为什么要使用xml呢？不能使json或者其他通用数据
  • js年份下拉框 3213213333332132 java web ee
    <div id="divValue">test...</div>测试 //年份 <select id="year"></select> <script type="text/javascript"> window.onload =
  • 简单链式调用的实现技术 归来朝歌 方法调用链式反应编程思想
    在编程中，我们可以经常遇到这样一种场景：一个实例不断调用它自身的方法，像一条链条一样进行调用 这样的调用你可能在Ajax中，在页面中添加标签： $("<p>").append($("<span>").text(list[i].name)).appendTo("#result");   也可能在HQ
  • JAVA调用.net 发布的webservice 接口 darkranger webservice
    /** * @Title: callInvoke * @Description: TODO(调用接口公共方法) * @param @param url 地址 * @param @param method 方法 * @param @param pama 参数 * @param @return * @param @throws BusinessException
  • Javascript模糊查找 | 第一章 循环不能不重视。 aijuans Way
    最近受我的朋友委托用js+HTML做一个像手册一样的程序，里面要有可展开的大纲，模糊查找等功能。我这个人说实在的懒，本来是不愿意的，但想起了父亲以前教我要给朋友搞好关系，再加上这也可以巩固自己的js技术，于是就开始开发这个程序，没想到却出了点小问题，我做的查找只能绝对查找。具体的js代码如下： function search(){ var arr=new Array("my
  • 狼和羊，该怎么抉择 atongyeye 工作
    狼和羊，该怎么抉择 在做一个链家的小项目，只有我和另外一个同事两个人负责，各负责一部分接口，我的接口写完，并全部测联调试通过。所以工作就剩下一下细枝末节的，工作就轻松很多。每天会帮另一个同事测试一些功能点，协助他完成一些业务型不强的工作。 今天早上到公司没多久，领导就在QQ上给我发信息，让我多协助同事测试，让我积极主动些，有点责任心等等，我听了这话，心里面立马凉半截，首先一个领导轻易说
  • 读取android系统的联系人拨号 百合不是茶 androidsqlite数据库内容提供者系统服务的使用
           联系人的姓名和号码是保存在不同的表中,不要一下子把号码查询来,我开始就是把姓名和电话同时查询出来的,导致系统非常的慢   关键代码:     1, 使用javabean操作存储读取到的数据 package com.example.bean; /** * * @author Admini
  • ORACLE自定义异常 bijian1013 数据库自定义异常
    实例： CREATE OR REPLACE PROCEDURE test_Exception ( ParameterA IN varchar2, ParameterB IN varchar2, ErrorCode OUT varchar2 --返回值,错误编码 ) AS /*以下是一些变量的定义*/ V1 NUMBER; V2 nvarc
  • 查看端号使用情况 征客丶 windows
    一、查看端口 在windows命令行窗口下执行： >netstat -aon|findstr "8080" 显示结果： TCP     127.0.0.1:80         0.0.0.0:0    &
  • 【Spark二十】运行Spark Streaming的NetworkWordCount实例 bit1129 wordcount
    Spark Streaming简介   NetworkWordCount代码   /* * Licensed to the Apache Software Foundation (ASF) under one or more * contributor license agreements. See the NOTICE file distributed with
  • Struts2 与 SpringMVC的比较 BlueSkator struts2spring mvc
    1. 机制：spring mvc的入口是servlet，而struts2是filter，这样就导致了二者的机制不同。 2. 性能：spring会稍微比struts快。spring mvc是基于方法的设计，而sturts是基于类，每次发一次请求都会实例一个action，每个action都会被注入属性，而spring基于方法，粒度更细，但要小心把握像在servlet控制数据一样。spring
  • Hibernate在更新时，是可以不用session的update方法的(转帖） BreakingBad Hibernateupdate
    地址：http://blog.csdn.net/plpblue/article/details/9304459 public void synDevNameWithItil() {Session session = null;Transaction tr = null;try{session = HibernateUtil.getSession();tr = session.beginTran
  • 读《研磨设计模式》-代码笔记-观察者模式 bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ import java.util.ArrayList; import java.util.List; import java.util.Observable; import java.util.Observer; /** * “观
  • 重置MySQL密码 chenhbc mysql重置密码忘记密码
    如果你也像我这么健忘，把MySQL的密码搞忘记了，经过下面几个步骤就可以重置了（以Windows为例，Linux/Unix类似）： 1、关闭MySQL服务 2、打开CMD，进入MySQL安装目录的bin目录下，以跳过权限检查的方式启动MySQL mysqld --skip-grant-tables  3、新开一个CMD窗口，进入MySQL mysql -uroot  
  • 再谈系统论，控制论和信息论 comsci 设计模式生物能源企业应用领域模型
                               再谈系统论，控制论和信息论     偶然看
  • oracle moving window size与 AWR retention period关系 daizj oracle
    转自： http://tomszrp.itpub.net/post/11835/494147 晚上在做11gR1的一个awrrpt报告时,顺便想调整一下AWR snapshot的保留时间,结果遇到了ORA-13541这样的错误.下面是这个问题的发生和解决过程. SQL> select * from v$version; BANNER -------------------
  • Python版B树 dieslrae python
    话说以前的树都用java写的,最近发现python有点生疏了,于是用python写了个B树实现,B树在索引领域用得还是蛮多了,如果没记错mysql的默认索引好像就是B树... 首先是数据实体对象,很简单,只存放key,value class Entity(object): '''数据实体''' def __init__(self,key,value)
  • C语言冒泡排序 dcj3sjt126com 算法
    代码示例： # include <stdio.h> //冒泡排序 void sort(int * a, int len) { int i, j, t; for (i=0; i<len-1; i++) { for (j=0; j<len-1-i; j++) { if (a[j] > a[j+1]) // >表示升序
  • 自定义导航栏样式 dcj3sjt126com 自定义
    -(void)setupAppAppearance { [[UILabel appearance] setFont:[UIFont fontWithName:@"FZLTHK—GBK1-0" size:20]]; [UIButton appearance].titleLabel.font =[UIFont fontWithName:@"FZLTH
  • 11.性能优化-优化-JVM参数总结 frank1234 jvm参数性能优化
    1.堆 -Xms --初始堆大小 -Xmx --最大堆大小 -Xmn --新生代大小 -Xss --线程栈大小 -XX:PermSize  --永久代初始大小 -XX:MaxPermSize  --永久代最大值 -XX:SurvivorRatio --新生代和suvivor比例,默认为8 -XX:TargetSurvivorRatio --survivor可使用
  • nginx日志分割 for linux HarborChung nginxlinux脚本
    nginx日志分割 for linux 默认情况下，nginx是不分割访问日志的，久而久之，网站的日志文件将会越来越大，占用空间不说，如果有问题要查看网站的日志的话，庞大的文件也将很难打开，于是便有了下面的脚本   使用方法，先将以下脚本保存为 cutlog.sh，放在/root 目录下，然后给予此脚本执行的权限   复制代码代码如下: chmo
  • Spring4新特性——泛型限定式依赖注入 jinnianshilongnian springspring4泛型式依赖注入
    Spring4新特性——泛型限定式依赖注入 Spring4新特性——核心容器的其他改进 Spring4新特性——Web开发的增强 Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC  Spring4新特性——Groovy Bean定义DSL Spring4新特性——更好的Java泛型操作API  Spring4新
  • centOS安装GCC和G++ liuxihope centosgcc
    Centos支持yum安装，安装软件一般格式为yum install .......，注意安装时要先成为root用户。 按照这个思路，我想安装过程如下： 安装gcc：yum install gcc 安装g++： yum install g++ 实际操作过程发现，只能有gcc安装成功，而g++安装失败，提示g++ command not found。上网查了一下，正确安装应该
  • 第13章 Ajax进阶（上） onestopweb Ajax
    index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
  • How to determine BusinessObjects service pack and fix pack blueoxygen BO
    http://bukhantsov.org/2011/08/how-to-determine-businessobjects-service-pack-and-fix-pack/   The table below is helpful. Reference   BOE XI 3.x 12.0.0. y BOE XI 3.0 12.0. x. y BO
  • Oracle里的自增字段设置 tomcat_oracle oracle
    　大家都知道吧，这很坑，尤其是用惯了mysql里的自增字段设置，结果oracle里面没有的。oh，no 　　我用的是12c版本的，它有一个新特性，可以这样设置自增序列，在创建表是，把id设置为自增序列 create table t ( id 　　 　　 number generated by default as identity (start with 1 increment b
  • Spring Security（01）——初体验 yang_winnie springSecurity
    Spring Security（01）——初体验     博客分类： spring Security Spring Security入门安全认证        首先我们为Spring Security专门建立一个Spring的配置文件，该文件就专门用来作为Spring Security的配置
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他