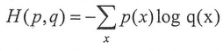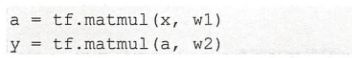TensorFlow知识点备忘1(随学习更新)
PS:本人初学,技术菜的抠脚,本博客仅对学习过程中遇到的知识点进行总结,如有错误,还望指出,谢谢。
1、Softmax层
功能:
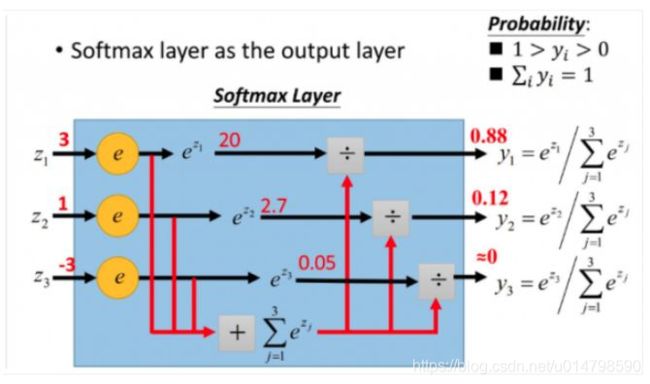
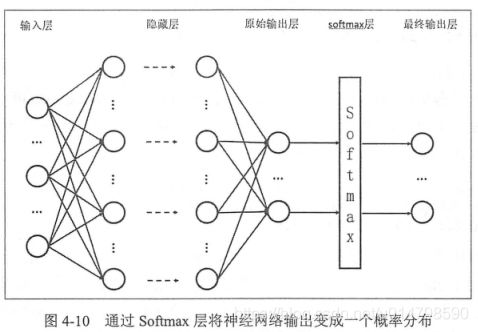
实现对神经网络输出结果进行归一化处理,将各结果概率限制在(0-1),并且概率和为1,同时对结果的置信度,转换为正值(使用以e为底的指数函数实现)。归一化公式见下图1
实现 1:
out1 = tf.random.normal([1,3])
out2 = tf.nn.softmax(out1, axis=1) # 通过 softmax 函数转换为概率值
print('out1:',out1)
print('out2:',out2)
#输出结果
out1: tf.Tensor([[ 1.541175 -0.744601 -1.2343484]], shape=(1, 3), dtype=float32)
out2: tf.Tensor([[0.8590977 0.08736602 0.05353626]], shape=(1, 3), dtype=float32)
实现2:
#模型的线性输出logits。附加一个softmax层,将输出转换为概率。
probability_model = tf.keras.Sequential([model, tf.keras.layers.Softmax()])
#模型对测试集中每个图像的标签进行预测处理
predictions = probability_model.predict(test_images)
print(predictions[0])#验证预测概率
参考资料:
《Tensorflow深度学习》——龙龙老师
《TensorFlow:实战Google深度学习框架(第2版)》——作者: 顾思宇 / 梁博文 / 郑泽宇
一分钟理解softmax函数(超简单)
2、Activation(激活函数)
功能:
神经元结构的输出为所有输入的加权和,这导致整个神经网络是一个线性模型。如果将每一个神经网络中节点的输出通过一个非线性函数,那么整个神经网络的模型也就不再是线性的了。这个非线性函数就是激活函数。
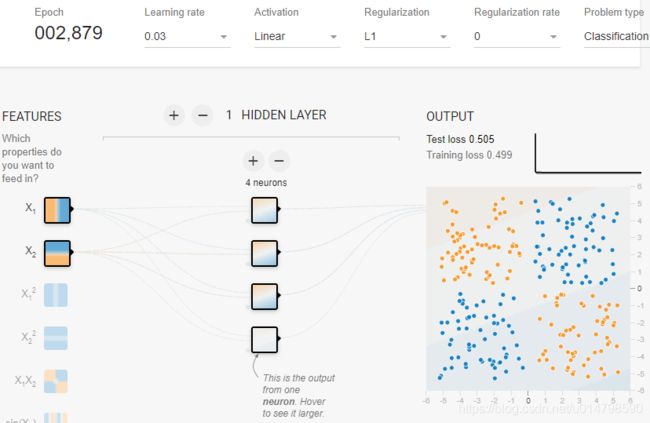
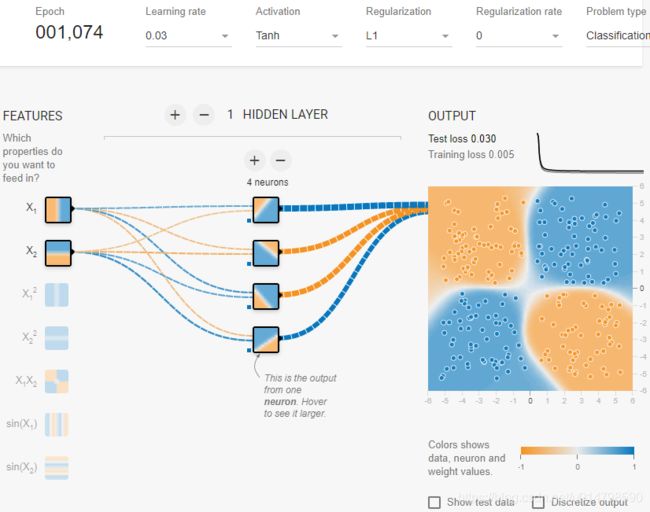
简单来说,对于一些无法用线性模型解决的问题(如下图1),就需要引入激活函数(非线性),来提高模型的表达能力(效果如下图2,可以看到只训练了1000多步,就达到了较好的训练精度)
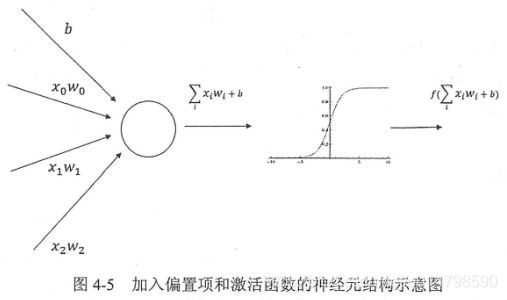
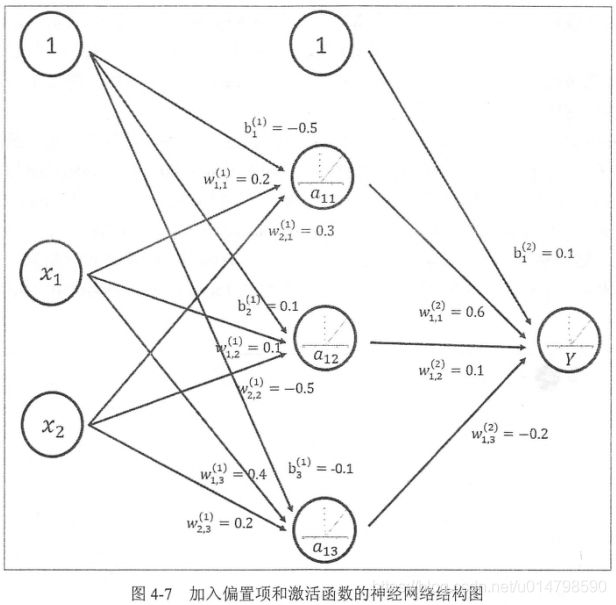
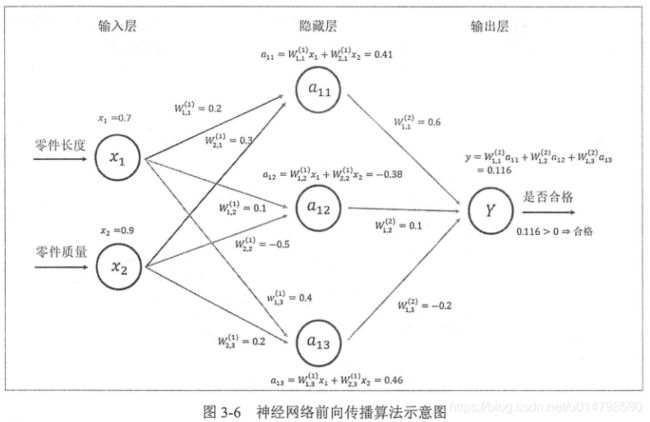
以下图3可以看出激活函数使用方法,先将节点值加上一个偏置值(bias),再将节点的输出在加权和的基础上做非线性变换(下图3使用ssigmoid激活函数)
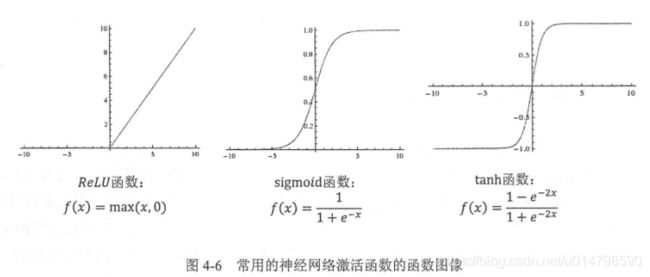
下图5给出了几种常用的激活函数的公式及函数图像
1实现:
x = tf.linspace(-6.,6.,10)
x=tf.nn.sigmoid(x) # 通过 Sigmoid函数
print('x:',x)
1输出:
x: tf.Tensor(
[0.00247262 0.00931596 0.0344452 0.11920292 0.33924368 0.6607564
0.880797 0.96555483 0.99068403 0.9975274 ], shape=(10,), dtype=float32)
2实现:
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),#指定输入数据的尺寸
keras.layers.Dense(128, activation='sigmoid'),#128个隐藏神经元的全连接层,激活函数使用relu
keras.layers.Dense(10)#设定输出层为10(标签为10)
])
参考资料:
激活函数(ReLU, Swish, Maxout)
激活函数sigmoid、tanh、relu、Swish
《TensorFlow:实战Google深度学习框架(第2版)》——作者: 顾思宇 / 梁博文 / 郑泽宇
playground.tensorflow(图一、图二生成网站)
3、Metrics(评估标准)
4、Loss(损失函数)
常见的损失函数有均方差(MSE)、交叉熵(Cross Entropy)、KL散度、Hinge
Loss函数等,其中均方差和交叉熵在深度学习中较为常见,均方差主要用于回归问题,而交叉熵主要用于分类问题。
均方差函数通过计算两个点之间的欧氏距离【(yi-y’i)^2】,来判断两个向量的差异。
MSE的结算结果总是大于等于0,当等于0时,表示误差为0,神经网络达到最优。
下式中yi为第i个数据所表示的正确答案,而y’i则为预测值。
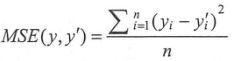
实现1
import tensorflow as tf # 导入tensorflow
from tensorflow import keras
o = tf.random.normal([2,10]) # 构造网络输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
loss1 = keras.losses.MSE(y_onehot, o) # 计算均方差
loss2=tf.reduce_mean(loss1)#计算平均
print(o)
print('loss1:',loss1)
print('loss2:',loss2)
输出结果:
tf.Tensor(
[[ 2.0084653 1.1281716 -0.563963 -0.6712413 -1.7490412 -0.3848372
-0.5653544 0.9210517 -0.12502158 0.7704787 ]
[ 0.53213567 -1.0841882 1.4143159 0.51209307 2.2036946 -0.1024802
1.4428381 2.7043867 -0.7862292 -0.5545245 ]], shape=(2, 10), dtype=float32)
loss1: tf.Tensor([0.98034555 1.888489 ], shape=(2,), dtype=float32)
loss2: tf.Tensor(1.4344172, shape=(), dtype=float32)
参考资料:
常见的损失函数(loss function)总结
损失函数 - 交叉熵损失函数
常用损失函数小结
MSE(均方误差)函数和RMSE函数
5、Dense(全连接层)
全连接层的本质是矩阵的相乘和相加运算,简单来说,就是每一个神经网络中的隐含层,输入为上一层的全部节点,输出为下一层的全部节点。
6、Cross Entropy(交叉熵)
PS:交叉熵也属于损失函数中的一类
交叉熵刻画了两个概率分布之间的距离,是分类问题中使用得较多得一种损失函数。
其公式(H(p,q)≠H(q,p)),所表达得是通过概率分布q来表达概率分别p的困难程度,当交叉熵作为神经网络的损失函数时,p代表的时正确答案,q代表的是预测值,交叉熵的值越小,两个概率分布越接近。

数学实现:一个三分类问题,正确答案是(1,0,0)。经过softmax层处理后,预测答案是(0.5,0.4,0.1),那么这个预测值和正确答案的交叉熵为:

可以看出,第二个预测结果的答案更接近真实值,交叉熵的计算结果也验证了这点。
代码实现1:
Step1:为了避免运算错误,如log0时无效及概率>1等问题,所以需要使用tf.clip_by_value()对数值限制在一个范围内。
v=tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
x=tf.clip_by_value(v,2.5,4.5)
print(x)
#输出结果
tf.Tensor(
[[2.5 2.5 3. ]
[4. 4.5 4.5]], shape=(2, 3), dtype=float32)
Step2:求对数
v=tf.constant([1.0,2.0,3.0])
x=tf.math.log(v)
print(x)
#输出结果:
tf.Tensor([0. 0.6931472 1.0986123], shape=(3,), dtype=float32)
Step3:矩阵各对应位的元素相乘
v1=([1.0,2.0],[3.0,4.0])
v2=([5.0,6.0],[7.0,8.0])
print(tf.multiply(v1,v2))#矩阵内各对应位的元素相乘并相加
#输出结果
#[1,1]:1x5=5
#[1,2]:2x6=12
tf.Tensor(
[[ 5. 12.]
[21. 32.]], shape=(2, 2), dtype=float32)
交叉熵一般与softmax层一起使用,所以可以使用TF所提供的针对分类问题的函数
代码实现2:
z = tf.random.normal([2,10]) # 以随机数构造输出层
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10) # one-hot 编码
# 输出层未使用 Softmax 函数,故 from_logits 设置为 True
# 这样 categorical_crossentropy 函数在计算损失函数前,会先内部调用 Softmax 函数
loss = keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)
loss = tf.reduce_mean(loss) # 计算平均交叉熵损失
print('z:',y_onehot)
print('y_onehot:',y_onehot)
print('loss:',loss)
#输出结果
z: tf.Tensor(
[[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]], shape=(2, 10), dtype=float32)
y_onehot: tf.Tensor(
[[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]], shape=(2, 10), dtype=float32)
loss: tf.Tensor(2.4338682, shape=(), dtype=float32)
引用资料:《TensorFlow:实战Google深度学习框架(第2版)》——作者: 顾思宇 / 梁博文 / 郑泽宇
7、Forward Propagation(前向传播)
import tensorflow as tf # 导入tensorflow
from tensorflow import keras
x = tf.random.normal([1,784])
print(x.shape)
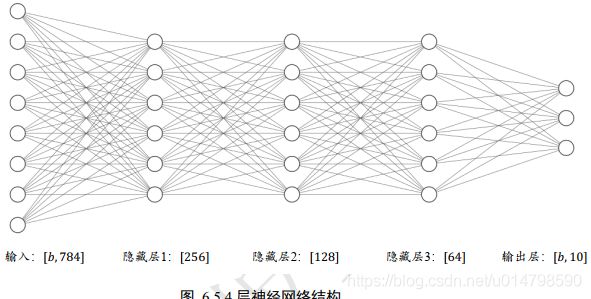
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),#指定输入数据的尺寸
keras.layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层1
keras.layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层2
keras.layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层3
keras.layers.Dense(10, activation=tf.nn.sigmoid) , # 创建输出层
])
out =tf.nn.softmax(model(x)) # 前向传播计算,并使用softmax对结果进行归一化处理
print(out)
#输出结果
tf.Tensor(
[[0.07505497 0.08324341 0.11679572 0.09662873 0.12196486 0.09430953
0.10640778 0.12813208 0.08211657 0.09534641]], shape=(1, 10), dtype=float32)
8、Backpro Pagation(反向传播/BP网络)
需要注意的是,本文第8、9、10小节应为一个整体,为方便理解,分开参数。
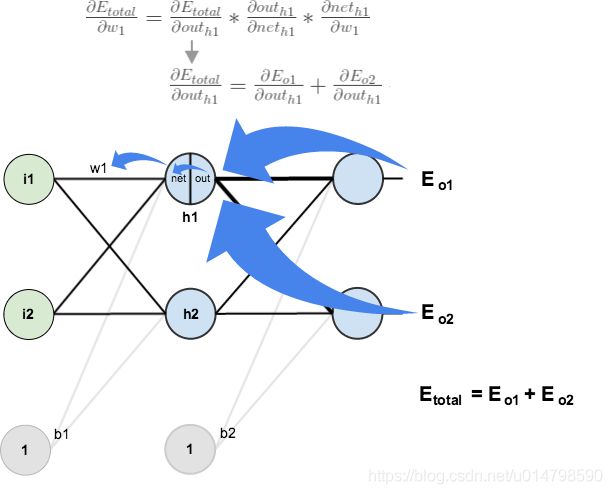
反向传播算法能以一个高效的方式在所有的参数上使用梯度下降算法,其可以根据定义好的损失函数优化神经网络中参数的取值,从而使得损失函数达到一个较小的数值
“正向传播”求损失,“反向传播”回传误差
神经网络优化过程可以分为两个阶段,第一阶段就是通过前向传播算法,计算得到预测值,并计算预测值和真实值的差距(损失函数);第二阶段就是通过反向传播算法计算损失函数对每个参数的梯度,再根据梯度和学习率,更新每一个参数。
参考资料:
“反向传播算法”过程及公式推导(超直观好懂的Backpropagation)
【机器学习笔记20】神经网络(链式求导和反向传播)
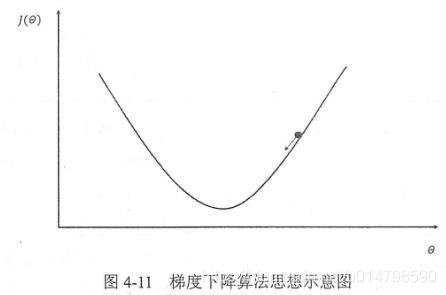
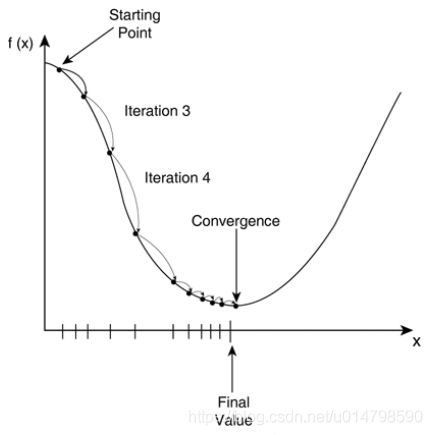
9、Gradient Decent(梯度下降算法)
梯度下降算法主要用于优化单个参数的取值,从而使模型在训练数据上的损失函数尽可能小。参数的梯度可以通过求偏导的方式进行计算,而学习率用于定义每次参数更新的幅度。
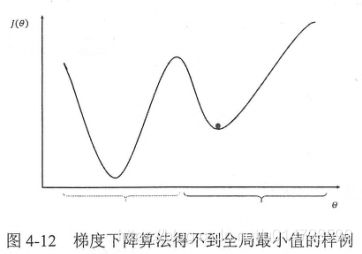
梯度下降算法并不能保证被优化的函数达到全局最优,而有可能只会得到局部最优,参数的初始值会很大程度影响最后得到的结果,只有当损失函数为凸函数时,梯度下降算法才能保证达到全局最优解
由于梯度下降算法需要计算全部训练数据的损失函数,这会造成大量时间的浪费,在此基础上,可以采用随机梯度下降算法,这个算法优化的不是全部训练数据上的损失函数,而是在每次迭代中,随机优化某一条训练数据上的损失函数,但该方法可能会造成神经网络甚至无法达到全局最优。
数学实现:
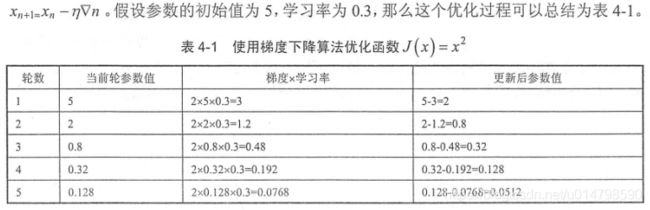
假设损失函数为J(x)=x^2,x的初始值由随机数产生,再通过梯度和学习率对参数x更新,x的梯度为下式
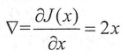
参考资料:
导数、偏导数、方向导数、梯度、梯度下降
10、Learning Rate(学习率)
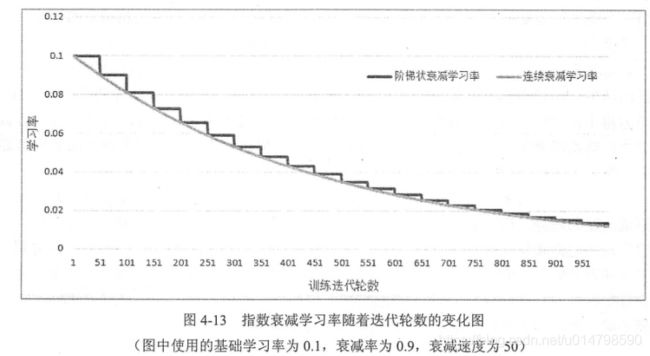
学习率用于控制每次梯度下降的幅度,如果幅度过大,可能造成参数在极值两侧震荡。以梯度下降算法所设定的J(x)=x^2为例子,如果学习率设定为1,则参数将难以收敛,如果学习率设定过小,则消耗时间过长。
为解决这个问题,可以采用指数衰减法,其思路如下图所示,开始使用较大的学习率来达到较优解,再逐步减小学习率,使模型能更快收敛。