POJ 2559-Largest Rectangle in a Histogram 解题报告 【笛卡尔树与单调栈】

POJ 2559-Largest Rectangle in a Histogram 解题报告 【笛卡尔树与单调栈】

Description

  A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

  Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

  The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that $1\le n\le 100000$ . Then follow n integers $h_1,...,h_n$ , where $0\le h_i\le 1000000000$ . These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

  For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

---

思路

  在网上看的很多题解，大多数都是利用“单调栈”来求解的。这里的“单调栈”也是基于栈的数据结构，只是在进行栈操作的时候需要满足栈内的元素单调递增（递减）。然而自己直接看题解里栈上的入栈、出栈操作，有点难以理解这种算法，跟着算法的步骤走了一遍也难以证明为什么这种算法就是对的。
  一种好理解的思路如图1所示，因为要比较所有可以向两方延展的矩形，所以先取高度最小的矩形，必定能向两边延展到最大范围；由于是高度最小的矩形，其左边区域的所有矩形不能跨过它向右延展，其右边区域的所有矩形不能跨过它向左延展，这样区域就分成了两块；问题就变成了递归求范围内高度最小的矩形。
  求 $logn$ 个范围内高度最小的矩形，最简单的想法就是依次遍历 $logn$ 个范围内的各个值求最小值，时间复杂度 $O(n\cdot logn)$ 。下面讲的笛卡尔树满足上述的结构，并且可以在 $O(n)$ 时间内建树。

图1 递归求解思路

---

笛卡尔树

  笛卡尔树^[1]满足下列性质：
    1.笛卡尔树中的结点对应序列中的每个值。
    2.树的中序遍历就是原序列。
    3.具有堆的性质：每个非根结点的父节点都比其大（或者小）。
  由上述的定义可以知道根结点是序列中最大（或者最小）的值，左子树和右子树也符合这个定义。

建树

  以小根堆的笛卡尔树举例：按照笛卡尔树的性质，笛卡尔树中序遍历就是原序列，所以后续插入的结点只能是某个结点的右结点，所以需要从根结点开始依次对比其右结点，直到找到符合堆性质的位置。插入的结点放在找到位置，改变了的目前堆性质的子树放在新结点的左边。
  如图2所示，以在现有的笛卡尔树中插入值为1*的结点，先从根节点开始，再依次对比其右结点，直到找到符合堆性质的插入位置。由于是之后插入的，所以1*需要是1的右结点；1的右子树比1*先插入，所以为1*的左结点。
  由于每次需要对比根结点即其右结点，所以维护这么一个栈即可。移到插入结点左边的结点即为出栈操作。每个元素最多执行一次入栈和出栈操作，所以时间复杂度为 $O(n)$ 。

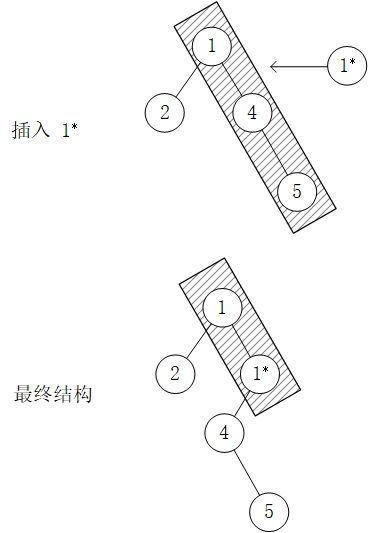
图2 插入操作

---

利用笛卡尔树求解

  建立好笛卡尔树后，因为每个矩形宽度为1，所以每个向两边延展的矩形的宽度为 左子树的结点个数+右子树结点个数+自身宽度1，递归遍历更新最大值即可。

#include 

typedef struct TreeNode
{
	int height;
	TreeNode* left, * right, *parent;
}TreeNode;

int index = 0;
TreeNode nodes[100000];

long long int max = 0;
long long int DFS(TreeNode* root)
{
	if (root == NULL)
		return 0;

	long long int width = (1 + DFS(root->left) + DFS(root->right));
	long long int S = width * root->height;
	if (S > max)
		max = S;

	return width;
}

int main()
{
	int N = 0;
	scanf("%d", &N);

	int height = 0;
	TreeNode* stack = NULL, *root = NULL, *p;

	while (N != 0)
	{
		stack = NULL;
		root = NULL;
		index = 0;

		for (; N > 0; N--)
		{
			scanf("%d", &height);
			while (stack && height < stack->height)
				stack = stack->parent;

			nodes[index].height = height;
			nodes[index].left = nodes[index].right = nodes[index].parent = NULL;
			if (stack)
			{
				nodes[index].parent = stack;
				nodes[index].left = stack->right;
				stack = stack->right = &nodes[index++];
				
			}
			else
			{
				stack = &nodes[index++];
				stack->left = root;
				root = stack;
			}
		}

		max = 0;
		DFS(root);
		printf("%lld\n", max);
		//
		scanf("%d", &N);
	}
}

---

利用单调栈求解

  由于笛卡尔树在建树的过程中就用到了单调栈，所以单调栈的思路就是不等树建好再去遍历求解，而是边建边求结果，直接自下而上，可省下用来存储树结点的空间。
  从建树的算法中发现，移到插入结点左结点的子树就不会改变了，递归求解也是将子树的值回升传递给父结点，所以在用栈建树的时候如果遇到出栈操作就可以进行回升操作了，并把值传递给父节点（插入结点）。

#include 

typedef struct
{
	int height;
	int width;
}Node;

int sp = 0;
Node stack[100000];

int main()
{
	int N = 0;

	scanf("%d", &N);
	int height = 0;
	int rise_width;
	long long int max, S;

	while (N != 0)
	{
		max = 0;
		sp = 0;
		for (; N > 0; N--)
		{
			scanf("%d", &height);
			rise_width = 0;
			while (sp > 0 && height < stack[sp - 1].height)
			{
				S = ((long long int)stack[sp - 1].height) * (stack[sp - 1].width + rise_width);
				if (S > max)
					max = S;
				rise_width += stack[sp - 1].width; //回升

				sp--;
			}

			stack[sp].height = height;
			stack[sp].width = 1 + rise_width;
			sp++;
		}

		rise_width = 0;
		while (sp > 0)
		{
			S = ((long long int)stack[sp - 1].height) * (stack[sp - 1].width + rise_width);
			if (S > max)
				max = S;
			rise_width += stack[sp - 1].width; //回升

			sp--;
		}

		printf("%lld\n", max);
		//
		scanf("%d", &N);
	}
}

参考

[1] 维基百科：笛卡尔树