链表：顺序表、单链表、循环链表、双向链表

内部结点唯一的前驱和后继，表头 只有后继，表尾只有前驱。

1、线性结构

线性表：顺序表（数组）、链表

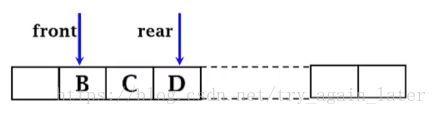
栈：插入和删除都限制在表的同一端进行（后入先出）

队列：插入在一端，删除在另一端（先进先出）

//线性表类模板如下，是顺序表类和链表类的基类,用虚函数virtual
template 
//value的类型是T
class LinearList
{
	virtual void clear() const=0;//置空线性表
	virtual bool isEmpty() const=0;//线性表为空时，返回true
	//增
	virtual bool append(const T value)=0;//表尾添加一个元素value
	virtual bool insert(const int p, const T value)=0;//位置p上插入元素value
	//删
	virtual bool delete(const int p)=0;//删除位置p上元素
	//改
	virtual bool setValue(cosnt int p, const T value)=0;//用value修改位置p的元素值
	//查
       virtual bool getPos(int& p, const T value) const=0;//查找元素为value的元素并返回其位置

       virtual bool getValue(const int p, T& value) const=0;//把位置p元素返回变量value
       virtual bool find(const int p, T& value) const = 0;//在x中返回表中下标为i的元素。若存在则返回true
};

2、顺序表

//顺序表，继承线性表
template 
class arrList :public LinearList
{
private:
	T* alist;//指向顺序表的指针
	int maxSize;//顺序表最大长度
	int curLen;//当前长度
	int position;//当前位置
public:
	//构造函数创建新表，设置表实例的最大长度
	arrList(const int size)
	{
		maxSize = size;
		alist = new T[maxSize];//new一个数组空间
		curLen = position = 0;
	}
	//析构函数
	~arrList()
	{
		delete[] alist;
	}
};

查找：

//在value中返回表中下标为p的元素
virtual bool find(const int p, T& value) const
{
	if (p<0 || p>this->n)
	{
		cout << "out of bounds" << endl;
		return false;
	}
	value = islist[p];
	return true;
}

插入：

template 
//定义插入
//p为新元素value的插入位置，插入成功则返回true
//curLen表示当前总长度
bool arrList::insert(const int p, const T value)
{
	int i;
	if (curLen >= maxSize)//溢出
	{
		return false;
	}
	if (p<0 || p>curLen)//插入位置是否合法
	{
		return false;
	}
        //数组需要遍历操作，从表尾向上走
	for (i = curLen; i > p; i--)
	{
		alist[i] = alist[i - 1];//从表尾curLen-1起向后移动直到p
	}
		alist[p] = value;//位置p处插入新元素
		curLen++;//表的实际长度+1
}

删除：

template 
//定义删除
//p为即将删除元素的位置，插入成功则返回true
//curLen表示当前总长度
bool arrList::insert(const int p, const T value)
{
	int i;
	if (curLen <= 0)//是否为空
	{
		return false;
	}
	if (p<0 || p>curLen-1)//插入位置是否合法
	{
		return false;
	}
        //遍历，从当前位置开始向表尾
	for (i = p; i 

 

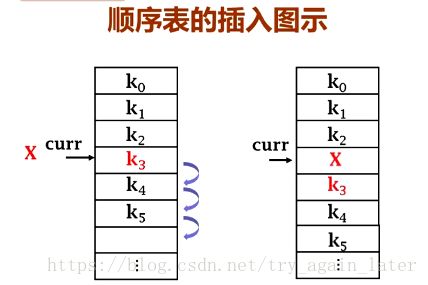
线性表的顺序表示是用一组地址连续的存储单元依次存储线性表中的元素。这样，逻辑上相邻的元素在物理上也相邻。顺序表是一种随机存取结构，但是插入和删除时效率较低，时间主要消耗在移动元素上。

插入移动n-i;删除移动n-i-1;

时间复杂度为O(n)

---

3、链表

单链表

哪里有空位就到哪里，大小不固定。

p->data数据元素；p->next指针

 

节点结构

C++ 结构体可以有构造函数。对于定义链表结点类型的结构来说，如果能给它提供一个或多个构造函数，那将会带来很大的方便，因为这样将使得结点在创建时即可初始化。

//结点类型
class Node
{
public:
	int data;//节点元素内容
	Node* next;//指向后继节点的指针
         //列表初始化构造函数
        Node():data(0),next(NULL){}
	Node(const int info,Node* next1 = NULL):data(info),next(next1){}
};

运算的分析：从第一个点开始

p=head;

while(p->next!=NULL）p=p->next

 

1、单链表的插入  O(1)

创建新节点->新节点指向右边的节点->左边节点指向新节点（不能倒过来，从后向前）

s->data=e; s->next=p->next; p->next=s;

// p节点后插入值为i的节点
void insertNode(Node* p,int i){
  Node* node=new Node;
  node->val=i;
  node->next=p->next;
  p->next=node;
}

2、单链表的删除  O(1)

将p下一个的节点覆盖到p节点即可，这样就等效于将p删除了。

void deleteNode(Node* p){
  p->val=p->next->val;
  p->next=p->next->next;
}

循环链表

唯一的区别就是它最后一个数据元素不指向NULL，而是指向头指针，这样的链表构成了一个环，因此成为循环链表

循环链表的操作和单链表基本一致，差别仅在于算法中的循环条件不是p->next!=NULL，

而是它们是否等于头指针p->next!=head.

总结：循环链表的目的是只要知道表中任一一个节点的地址，就能遍历表中其他任一节点。

双向链表

//结点类型
class Node
{
public:
	int data;//节点元素内容
        Node* prior;//前驱指针
	Node* next;//后继指针
         //列表初始化构造函数
        Node():data(0),next(NULL){}
	Node(const int info,Node* next1 = NULL):data(info),next(next1){}
};

 

插入

s->prior=p;
s->next=p->next;
p->next->prior=s;
p->next=s;

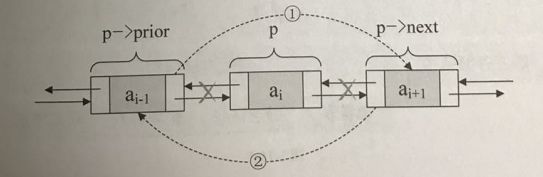
删除

p->prior->next=p->next;
p->next->prior=p->prior;
free(p);

注意：

头指针处理

非循环链表表尾节点的指针保持为NULL

循环链表结尾的指针回指头结点

插入删除少用顺序表，动态结点变化插入删除多用链表