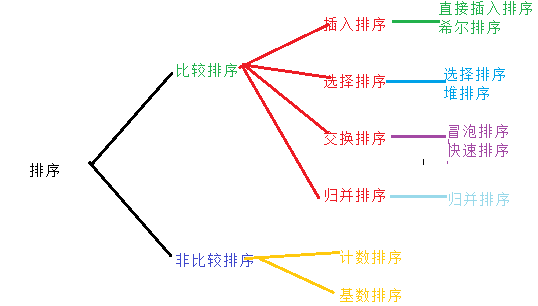
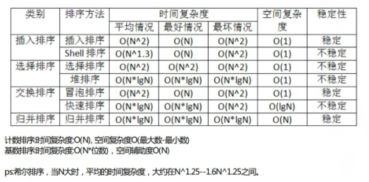
排序总结,插入排序 选择排序 交换排序 归并排序 计数排序 时间复杂度空间复杂度稳定性详解
排序大体分为两类:比较排序和非比较排序
一 各个排序的基本实现
1.直接插入排序和希尔排序
//整体思路:往一段有序区间插入元素,end标记为有序区间的最后一个元素下标,要插入的元素下标为end+1此处就称tmp,先把他保存起来,(否则可能被覆盖)如果end+1这个元素
//比有序区间的小,就把有序区间元素依次向后移动,移动结束条件有两个,1.end变为-1,2.有序区间内找到比tmp小的数。
void PrintArray ( int *a, size_t n )
{
for ( size_t i = 0; i < n ; i++ )
{
cout << a[i] << " ";
}
cout << endl;
}
//时间复杂度:o(N^2) 最坏情况,每次插入要把前面的全移动 1+2+....n-1等差数列求和(n-1)*n/2也就是o(N^2)逆序时最坏
// o(N) 顺序最好,只比较了一遍没进去
void InsertSort ( int *a, size_t n )
{
assert ( a );
for ( size_t i = 0; i < n-1; i++ )
{
int end = i;
//单趟逻辑
int tmp = a[end + 1];
while (end>=0&& a[end] >tmp )
{
a[end + 1] = a[end];
--end;
}
a[end + 1] = tmp;
}
}
//整体思路1.预排序(使大的数很快移到后面去)分组在每组内移动接近有序 gap越大越不接近有序 2.插入排序
//1.gap>1 预排序
//2.gap==1 插入排序
void ShellSort ( int*a, size_t n )//是针对插入排序逆序的情况下,移动次数太多而设计。 希尔排序用于数据量较大
{
assert ( a );
int gap=n;
//预排序:排完说明分组为gap的这些元素各自有序
while ( gap > 1 )
{
gap = gap / 3+1;//加1保证了最后一次为gap=1,绝对会有序
for ( size_t i = 0; i= 0 && a[end] > tmp )
{
a[end+gap] = a[end ];
end -= gap;
}
a[end + gap] = tmp;
}
}
}
void TestInsertSort ( )
{
int a[] = { 2, 5, 4, 9, 3, 6, 8, 7, 1 };
//InsertSort ( a, sizeof(a) / sizeof(a[0]));
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
void TestShellSort ( )
{
int a[] = { 2, 5, 4, 9, 3, 6, 8, 7, 1 };
ShellSort ( a, sizeof(a) / sizeof(a[0]));
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
} 2.选择排序和堆排序
//选择排序 每次可选一个最小的数,一个最大的数
//时间复杂度 最坏o(N^2) n-1+n-2+1 也是等差数列
//时间复杂度 最好o(N^2) 尽管你有序,可是我不知道还是要每次遍历一遍
void SelectSort ( int *a, size_t n )
{
int end = n-1;
int begin= 0;
while ( begin< end )
{
int min = begin;
int max = begin;
for ( size_t i = begin; i <= end; i++ )
{
if ( a[i]>a[max] )
{
max = i;
}
if ( a[i] < a[min ])
{
min = i;
}
}
/* swap ( a[min], a[begin] );
if (begin== max )
{
max = min;
}
swap ( a[max], a[end] );*/
swap ( a[max], a[end] );
if ( min == end )
{
min = max;
}
swap ( a[min], a[begin] );
begin++;
end--;
}
}
//堆排序 升序 建大堆,把最大的数选出来,换到后面去,然后把剩下的数向下调整看成一个堆
//选第一个数要建堆N*lg N 其他lgn 即N*lgN+(N-1)lgN=o(NlgN)
void AdjustDown ( int *a, size_t n, int root )
{
int parent = root;
int child = 2 * parent;
while ( child a[child] )
{
child++;
}
if ( a[child] > a[parent] )
{
swap ( a[child], a[parent] );
parent = child;
child = parent * 2;
}
else
{
break;
}
}
}
void HeapSort ( int *a, size_t n )
{
for ( int i = (n - 2) / 2; i >= 0; i-- )//建堆NlgN
{
AdjustDown ( a, n, i );//lgN
}
//(N-1)lgN
int end = n - 1;
while ( end > 0 )
{
swap ( a[0], a[end] );
AdjustDown ( a, end, 0 );
--end;
}
}
void TestHeapSort ( )
{
int a[] = { 2, 5, 4, 9, 3, 6, 8, 7, 1, 0 };
HeapSort ( a, sizeof(a) / sizeof(a[0]) );
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
void TestSelectSort ( )
{
int a[] = { 2, 5, 4, 9, 3, 6, 8, 7, 1 ,0};
SelectSort ( a, sizeof(a) / sizeof(a[0]));
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
int main ( )
{
//TestSelectSort ( );
TestHeapSort ( );
system ( "pause" );
return 0;
}
3.冒泡排序和快速排序
冒泡排序
//交换排序
//时间复杂度0(N^2) n-1+n-2+.....1 也是等差数列
//最好的情况下:0(N) 有序
//冒泡和插入的区别:插入比冒泡好,冒泡要求更严格的有序
//比如:123465 如果插入排序 是比较N-1次,插入一次 N 冒泡排序:第一趟比较 N-1次之后,已经有序可是不知道,又要来一遍 N-1
//因此插入比冒泡好,冒泡要求更严格有序
void BubbleSort ( int *a, size_t n )
{
//int end = n - 1;
//while ( end > 0 )
//{
// bool ExChange = 0;
// for ( size_t i = 0; i < end; i++ )//单趟
// {
// if ( a[i]>a[i + 1] )
// {
// swap ( a[i], a[i + 1] );
// ExChange = 1;
// }
// }
// if ( ExChange == 0 )
// {
// break;
// }
// end--;
//}
for ( size_t end = n - 1; end > 0; end-- )
{
bool ExChange = 0;
for ( size_t i = 0; i < end; i++ )//单趟
{
if ( a[i]>a[i + 1] )
{
swap ( a[i], a[i + 1] );
ExChange = 1;
}
}
if ( ExChange == 0 )
{
break;
}
}
}
void TestBubbleSort ( )
{
int a[] = { 2, 5, 4, 9, 3, 6, 8, 7, 1, 0 };
BubbleSort ( a, sizeof(a) / sizeof(a[0]) );
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
快速排序:
//时间复杂度:递归的次数乘以每次递归 递归的次数N每次递归lgN 因此时间复杂度为o(NlgN)
//最坏情况:0(N^2) 有序 三数取中法,解决了有序的这种情况
int GetMidindex ( int *a, int begin, int end )
{
int mid = begin + ((end - begin) >> 1);
if ( a[mid] > a[begin] )
{
if ( a[begin] > a[end] )
{
return begin;
}
else if ( a[mid] > a[end] )
{
return end;
}
else
{
return mid;
}
}
else
{
if ( a[begin] > a[end] )
{
return begin;
}
else if ( a[end] > a[mid] )
{
return mid;
}
else
{
return end;
}
}
}
//左右指针法
int PartSort2 ( int *a, int begin, int end )
{
//int& key= a[end];//为什莫给a[end]而不是和讲的一样是a[end-1],注意考虑有序情况:如果给a[end-1]反而错了,如果给a[end]就自己和自己交换
int mid = GetMidindex ( a, begin, end );
swap ( a[mid], a[end] );
int keyIndex = end;
int key = a[end];
while ( begin < end )
{
while ( begin=key )
{
end--;
}
swap ( a[end], a[begin] );
}
swap(a[keyIndex], a[begin]);
return begin;
}
//挖坑法
int PartSort1 ( int*a, int begin, int end )
{
int key = a[end];
while ( begin < end )
{
while (begin= key )
{
end--;
}
a[begin] = a[end];
}
a[begin] = key;
return begin;
}
//前后指针法
int PartSort3 ( int *a, int begin, int end )
{
int& key = a[end];
//int key=a[end]
int cur = begin;
int prev = begin - 1;
while ( cur < end )
{
if ( a[cur] < key && (++prev) != cur )
{
swap ( a[prev], a[cur] );
}
cur++;
}
swap ( a[++prev], key );//swap(a[++prev],a[end]);
return prev;
}
void QuicksortNonR ( int *a, int left, int right )
{
stackst;
st.push ( right );
st.push ( left );
while ( !st.empty ( ) )
{
int begin = st.top ( );
st.pop ( );
int end = st.top ( );
st.pop ( );
int div = PartSort3 ( a, begin, end );
if ( begin < div - 1 )
{
st.push ( div - 1 );
st.push ( begin );
}
if ( div + 1 < end )
{
st.push ( end );
st.push ( div + 1 );
}
}
}
void Quicksort ( int* a, int left,int right )
{
if ( left >= right )
{
return;
}
//小区间优化
if ( right - left < 8)//省去最后3层
{
InsertSort ( a+left, (right - left) + 1 );
return;
}
int div = PartSort3 ( a, left, right );
Quicksort ( a, left, div - 1 );
Quicksort ( a, div + 1, right );
}
//有序有两种情况:1.区间只剩一个值,说明有序
// 2.左边有序,右边有序
void TestQuickSort ( )
{
int a[] = { 5, 10, 4, 9, 20, 6, 8, 7, 1, 5 };
QuicksortNonR ( a, 0, sizeof(a) / sizeof(a[0]) - 1 );
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
//int main ( )
//{
// //TestBubbleSort ( );
//
// TestQuickSort ( );
// system ( "pause" );
// return 0;
//}
4.归并排序
归并排序
时间复杂度:0(NlgN) 空间复杂度:0(N)
void _MergeSort ( int *a, int left, int right, int* tmp )//tmp为什莫再外面开tmp,所有递归都可以用.如果在里面开里面每次递归都要开辟空间
{
if ( left >= right )//如果只剩一个元素,或者没有元素可以看作是有序的
{
return;
}
if ( right - left < 8 )//省去最后3层
{
InsertSort ( a + left, (right - left) + 1 );
return;
}
int div = ((right - left) >> 1) + left;
//让两段子区间有序再归并
//[left,div] [div+1 ,right]
_MergeSort ( a, left, div, tmp );
_MergeSort ( a, div + 1, right, tmp );
int index = left;
int begin1 = left; int end1 = div;
int begin2 = div + 1; int end2 = right;
while ((begin1<=end1)&&(begin2<=end2))
{
if ( a[begin1] <= a[begin2] )
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while( begin1 <= end1 )
{
tmp[index++] = a[begin1++];
}
while (begin2<=end2 )
{
tmp[index++] = a[begin2++];
}
//每次归并完,再拷贝到原区间上去
index = left;
while ( index <= right )
{
a[index] = tmp[index];
++index;
}
}
void MergeSort ( int *a,size_t n)
{
int * tmp = new int[n];
_MergeSort(a, 0, n - 1,tmp);
delete[]tmp;
}
void TestMergeSort ( )
{
int a[] = { 5, 10, 4, 9, 20, 6, 8, 7, 1, 5 };
MergeSort( a, sizeof(a) / sizeof(a[0]));
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
int main ( )
{
TestMergeSort ( );
system ( "pause" );
return 0;
}
5.计数排序
//非比较排序
//基数排序:只能用于排整型 不多讲
//计数排序:
//直接定址法的哈希
//时间复杂度 0(max(n,range)) 数据范围比较集中的时候适合用计数排序
void CountSort ( int *a, int n )
{
int max = a[0];
int min = a[0];
for ( int i = 0; i < n; i++ )
{
if ( a[i]>max )
{
max = a[i];
}
if ( a[i] < min )
{
min = a[i];
}
}
int range = max - min + 1;
int * hashtable = new int[range];//不能开n,是相对位置
memset ( hashtable, 0, sizeof(int)*range );
for ( size_t i = 0; i < n; i++ )
{
hashtable[a[i] - min]++;// a[i]是绝对位置,记清楚此处是相对位置
}
size_t j = 0;
for ( size_t i = 0; i < range; i++ )
{
while ( hashtable[i]-- )
{
a[j] = i + min;
++j;
}
}
delete[] hashtable;
}
void TestCountSort ( )
{
int a[] = { 5, 10, 4, 9, 20, 6, 8, 7, 1, 5 };
CountSort( a, sizeof(a) / sizeof(a[0]));
PrintArray ( a, sizeof(a) / sizeof(a[0]) );
}
int main ( )
{
TestCountSort ( );
system ( "pause" );
return 0;
}
二 时间复杂度和空间复杂度
三 稳定性
稳定性:应用场景:成绩排名:成绩相同,先交卷子在前,后交卷子在后
具体操作:先拿时间排,再拿一个稳定的的排序对成绩排,就能保证
各个排序的稳定性
各个排序的稳定性
首先要明白所有的稳定排序都可以变成不稳定的。
插入 稳定:我能做到比你小让你往后挪,和你相等放你后面如此便可以保证有序
希尔 不稳定:相同的值可能被分到不同的组里面 把相对顺序打乱
选择排序 不稳定 :先选到的放到最后面取
堆排序 不稳定:父亲大于等于孩子 把父亲的放到后面了,孩子的放次后面 相对位置变了
冒泡 稳定 :大的往后冒泡,相等不往后冒泡
快排 不稳定:比它大的往右翻,比它小的往左翻 最后后面的那个到中间 。 // 1 9 5 7 6 4 5 8 5
归并排序 稳定:如果相等时先拿左边的
插入 稳定:我能做到比你小让你往后挪,和你相等放你后面如此便可以保证有序
希尔 不稳定:相同的值可能被分到不同的组里面 把相对顺序打乱
选择排序 不稳定 :先选到的放到最后面取
堆排序 不稳定:父亲大于等于孩子 把父亲的放到后面了,孩子的放次后面 相对位置变了
冒泡 稳定 :大的往后冒泡,相等不往后冒泡
快排 不稳定:比它大的往右翻,比它小的往左翻 最后后面的那个到中间 。 // 1 9 5 7 6 4 5 8 5
归并排序 稳定:如果相等时先拿左边的