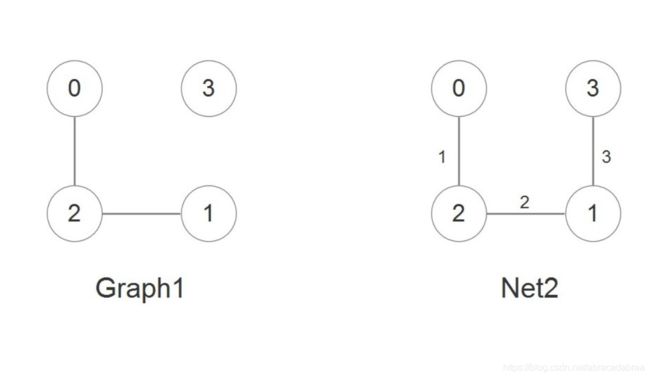
运用遍历判断无向图(网)是否连通
基本思路:
使用广度优先遍历方法,任选一个结点开始遍历,遍历结束后每个结点都访问到了即为连通。
主代码:
判断是否连通的isConnected()方法在最末尾。
import dataStructure.linearList.LinkQueue;
public class ALGraph<E> implements
IGraph<E> {
private GraphKind kind; //图的类型
private int vexNum; //图中顶点数
private int arcNum; //图中边(弧)数
private VNode<E> vexs[]; //图的顶点结点数组
public ALGraph() {
this(null,0,0,null);
}
public ALGraph(GraphKind kind, int vexNum, int arcNum, VNode<E>[] vexs) {
this.kind = kind;
this.vexNum = vexNum;
this.arcNum = arcNum;
this.vexs = vexs;
}
public GraphKind getKind() {
return kind;
}
public int getVexNum() {
return vexNum;
}
public int getArcNum() {
return arcNum;
}
public VNode<E>[] getVexs() {
return vexs;
}
//获取顶点位置序号为v的顶点的数据
public E getVex(int v) throws Exception {
if (v < 0 || v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
return vexs[v].getData();
}
//获取顶点数据为vex的顶点的位序号
public int locateVex(E vex) {
for (int i = 0; i < vexNum; i++)
if (vexs[i].getData().equals(vex))
return i;
return -1;
}
//获取位置序号为v的顶点的第一个邻接边对应的邻接点的位序号
public int firstAdjVex(int v) throws Exception {
if (v < 0 || v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
if (vexs[v].getFirstArc() != null) //它一条关联的边(或者有向图一条出边都没有)的话,空对象不能调用getAdjVex()方法,会报错
return vexs[v].getFirstArc().getAdjVex();
else
return -1;
}
//获取位置序号为v的顶点的位序号为w的邻接点的下一个邻接点
public int nextAdjVex(int v, int w) throws Exception {
if (v < 0 || v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
ArcNode arcVW = null;
ArcNode arc = vexs[v].getFirstArc();
while(arc != null) {
if(arc.getAdjVex() == w) {
arcVW = arc;
break;
}
else
arc = arc.getNextArc();
}
if (arcVW != null && arcVW.getNextArc() != null)
return arcVW.getNextArc().getAdjVex();
else
return -1;
}
//获取起始顶点位置序号为initVex,终止顶点位置序号为termVex的边(结点)
public ArcNode getArc (int initVex, int termVex) throws Exception {
if(initVex < 0 || initVex >= vexNum)
throw new Exception("第" + initVex + "个顶点不存在!");
if(termVex < 0 || termVex >= vexNum)
throw new Exception("第" + termVex + "个顶点不存在!");
ArcNode arc = vexs[initVex].getFirstArc(); //arc指向起始顶点的第一条边
while(arc != null && arc.getAdjVex() != termVex) {
arc = arc.getNextArc(); //arc指向起始顶点的下一条边
}
return arc;
}
//广度优先遍历
public void BFSTraverse() throws Exception {
boolean[] visited = new boolean[vexNum]; //初始化辅助数组visited
for(int i = 0; i < vexNum; i++) {
visited[i] = false;
}
LinkQueue<Integer> lq = new LinkQueue(); //创建辅助队列,数据元素为顶点的位置序号
for(int v = 0; v < vexNum; v++) { //依次访问图中的所有连通分量(或强连通分量)
if(!visited[v]) {
lq.offer(v); //指定顶点v入队
while(!lq.isEmpty()) {
int u = lq.poll(); //辅助队列队首顶点出队
System.out.print(vexs[u].getData() + " "); //访问该顶点
visited[u] = true; //标记该顶点为true
//将刚出队的顶点的所有未被访问的邻接点加入辅助队列中
for (int w = firstAdjVex(u); w>=0; w = nextAdjVex(u,w))
if(!visited[w])
lq.offer(w);
}
}
}
}
boolean isConnected() throws Exception {
if (kind!=GraphKind.UDG || kind!=GraphKind.UDN )
throw new Exception("该图不是无向图或无向网!");
//用遍历判断,如果从一个点开始循环访问不到所有结点的就是非连通图
//广度优先遍历求解
boolean[] visited = new boolean[vexNum]; //初始化辅助数组visited
for(int i = 0; i < vexNum; i++) {
visited[i] = false;
}
LinkQueue<Integer> lq = new LinkQueue(); //创建辅助队列,数据元素为顶点的位置序号
//访问本连通分量
if (!visited[0]) {
lq.offer(0); //第一个顶点入队
while (!lq.isEmpty()) {
int u = lq.poll(); //辅助队列队首顶点出队
visited[u] = true; //标记该顶点为true
//将刚出队的顶点的所有未被访问的邻接点加入辅助队列中
for(int w = firstAdjVex(u); w>=0; w = nextAdjVex(u,w))
if(!visited[w])
lq.offer(w);
}
}
//判断:如果所有结点访问到了就是连通的
for(int j = 0; j < vexNum ; j++) {
if(visited[j]==false)
return false;
}
return true;
}
}
测试:
import dataStructure.Graph.ALGraph;
import dataStructure.Graph.VNode;
import dataStructure.Graph.ArcNode;
import dataStructure.Graph.GraphKind;
/*
*本程序用来测试ALGraph类中的isConneted()方法
*Graph1,Net2的示意图见上图.jpg”。
*/
public class GraphTest {
public static void main(String[] args){
//一个非连通无向图Graph1
GraphKind kind1 = GraphKind.UDG;
int vexNum1 = 4;
int arcNum1 = 2;
ArcNode a1 = new ArcNode(2);
ArcNode b1 = new ArcNode(2);
ArcNode d1 = new ArcNode(1);
ArcNode c1 = new ArcNode(0,d1);
VNode<Integer> gnode0 = new VNode(0, a1);
VNode<Integer> gnode1 = new VNode(1, b1);
VNode<Integer> gnode2 = new VNode(2, c1);
VNode<Integer> gnode3 = new VNode(3);
VNode<Integer> vexs1[] = new VNode[4];
vexs1[0] = gnode0;
vexs1[1] = gnode1;
vexs1[2] = gnode2;
vexs1[3] = gnode3;
ALGraph<Integer> graph1 = new ALGraph(kind1,vexNum1, arcNum1, vexs1);
try{
System.out.println("graph1连通吗?"+graph1.isConnected());
}
catch(Exception e){ }
//一个连通无向网Net2
GraphKind kind2 = GraphKind.UDN;
int vexNum2 = 4;
int arcNum2 = 3;
ArcNode a2 = new ArcNode(2,1);
ArcNode c2 = new ArcNode(1,2);
ArcNode b2 = new ArcNode(0,1,c2);
ArcNode e2 = new ArcNode(3,3);
ArcNode d2 = new ArcNode(2,2,e2);
ArcNode f2 = new ArcNode(1,3);
VNode<Integer> nnode0 = new VNode(0, a2);
VNode<Integer> nnode1 = new VNode(1, d2);
VNode<Integer> nnode2 = new VNode(2, b2);
VNode<Integer> nnode3 = new VNode(3, f2);
VNode<Integer> vexs2[] = new VNode[4];
vexs2[0] = nnode0;
vexs2[1] = nnode1;
vexs2[2] = nnode2;
vexs2[3] = nnode3;
ALGraph<Integer> net2 = new ALGraph(kind2, vexNum2, arcNum2, vexs2);
try{
System.out.println("net2连通吗?"+net2.isConnected());
}
catch(Exception e){ }
}
}