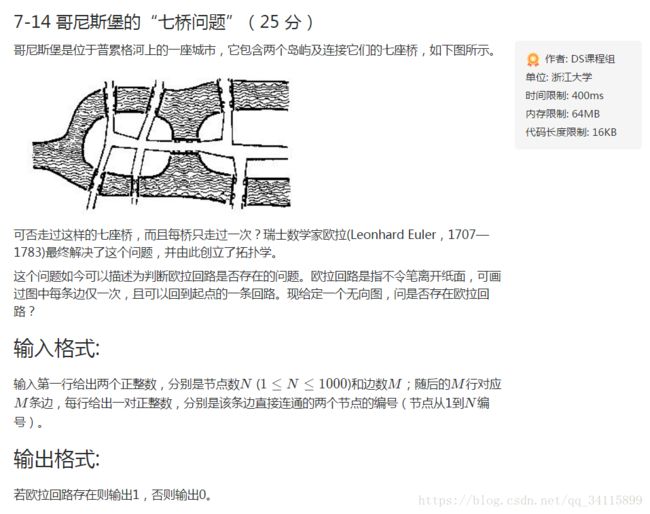
无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
#include
using namespace std;
int parent[1001]; // N个顶点
int degree[501001]; // 最多N*(N-1)/2条边
int height[1001];
int find(int p)
{
int root = p;
while (root != parent[root]) // 加权quick-union算法,找到根节点,父节点是自己的就是根节点
{
root = parent[root];
}
while (p != root) // 路径压缩,把查找的每个结点直接连接到根节点上
{
int newp = parent[p];
parent[p] = root;
p = newp;
}
return root;
}
void connected(int p, int q)
{
int i = find(p);
int j = find(q);
if (i == j)
return;
if (height[i] < height[j]) // 把高度较小的树连接到高度较大的树上
{
parent[i] = j;
height[j] += height[i];
}
else
{
parent[j] = i;
height[i] += height[j];
}
}
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i)
{
parent[i] = i;
}
for (int i = 0; i < m; ++i)
{
int v, w;
scanf("%d %d", &v, &w);
if (find(v) != find(w))
{
connected(v, w);
}
++degree[v]; // 只要有一条连接它的边,度就加1
++degree[w];
}
bool flag = true;
for (int i = 1; i <= n; ++i)
{
if (degree[i] & 1) // 如果顶点是奇数,不满足
{
flag = false;
break;
}
}
if (flag)
{
int temp = find(1);
for (int i = 2; i <= n; ++i) // 如果父亲为同一个,说明可以一笔画
{
if (temp != find(i))
{
flag = false;
break;
}
}
if (flag)
{
putchar('1');
}
else
{
putchar('0');
}
}
else
{
putchar('0');
}
return 0;
} 这个题目用java的话最后两个测试点过不去,可以自己写java对照试一试
========================================Talk is cheap, show me the code=======================================