NLP面试题总结(包含8种优化器简介).03
目录
part 1.
1. 介绍一下几种优化器
1.1 SGD(Stochastic Gradient Descent)
1.2 BGD(Batch Gradient Descent)
1.3 MBGD(Mini-Batch Gradient Descent)
1.4 Momentum
1.5 Adagrad(Adaptive gradient algorithm)
1.6 Adadelta
1.7 RMSprop
1.8 Adam(Adaptive Moment Estimation)
2. LSTM里面有哪些门,为什么用这些门?
3.LSTM里面为什么有些激活函数用sigmoid,有些用tanh?
4. Bert中的位置向量作用是什么?有哪些生成方式?
part 2.
1. 浅copy和深copy的概念
2. Python中的self关键字
3. Python中类的继承
4. 完全二叉树的概念
5. 单链表与顺序表的区别
6. 给出二叉树的前序遍历(preorder)和中序遍历(inorder),重建该二叉树:
7.反转一个链表,并返回头结点
part 1.
1. 介绍一下几种优化器
在机器学习与深度学习中,主要应用于梯度下降。如,传统的优化器主要结合数据集,通过变化单次循环所采用的数据量的大小对梯度下降进行控制;非传统的优化器则进一步集合数据集的特点和模型的训练时间,以不同的形式变化梯度下降的学习率。
常见的优化器有SGD、BGD、MBGD、Momentum、Adagrad、RMSprop、Adam。
梯度下降的原理:
![]()
其中,![]() 为学习率,
为学习率,![]() 为更新前的参数,
为更新前的参数,![]() 为更新后的参数,
为更新后的参数,![]() 为当前参数的导数。
为当前参数的导数。
1.1 SGD(Stochastic Gradient Descent)
SGD随机梯度下降参数更新原则:单条数据就可对参数进行一次更新。
优点:参数更新速度快。
缺点:由于每次参数更新时采用的数据量小,造成梯度更新时震荡幅度大,但大多数情况是向着梯度减小的方向。
for n in n_epochs:
for data in train_dataset:
#对参数进行一次更新1.2 BGD(Batch Gradient Descent)
BGD批量梯度下降参数更新原则:所有数据都参与梯度的每一次更新(一个batch中每个参数需要更新的梯度取均值作为更新值)。
优点:由于每次参数更新时采用的数据量大,所以梯度更新时比较平滑。
缺点:由于参数更新时需要的数据量大,造成参数更新速度慢。
for n in n_epochs:
for data in train_dataset:
#计算每个参数所有梯度的均值作为一次更新的梯度,对参数进行一次更新1.3 MBGD(Mini-Batch Gradient Descent)
MBGD小批量梯度参数更新原则:只有所有数据的一部分进行参数的更新。
优点:相比于SGD,由于参与梯度更新的数据量大,所以梯度更新时相对平滑;相比于BGD,参与梯度更新的数据量小,参数更新速度更快一些。
缺点:没有考虑到数据集的稀疏度和模型的训练时间对参数更新的影响。
n=0
while n <= n_epochs:
for minibatch_traindataset in train_dataset:
if n <= n_epochs:
n+=1
for i in minibatch_traindataset:
#计算每个参数更新的梯度的均值作为一次更新的梯度进行参数更新
else:break
1.4 Momentum
Momentum解决的问题是:SGD梯度下降时的震荡问题。
Momentum参数更新原则:通过引入 ![]() ,加速SGD,并且抑制震荡。(MBGD是通过小批量数据来平滑梯度更新,方法不同而已)
,加速SGD,并且抑制震荡。(MBGD是通过小批量数据来平滑梯度更新,方法不同而已)
更新公式:
![]()
![]()
超参数设定值:![]() 一般取 0.9 左右。
一般取 0.9 左右。
优点:通过加入 ![]() ,使得梯度方向不变的维度上速度变快,梯度方向改变的维度上更新速度变慢,这样就可以加快收敛并减小震荡。
,使得梯度方向不变的维度上速度变快,梯度方向改变的维度上更新速度变慢,这样就可以加快收敛并减小震荡。
缺点:梯度方向不变时,参数更新速度会越来越快,但是在梯度方向改变时,梯度更新速度不能及时减小导致适应性差。
1.5 Adagrad(Adaptive gradient algorithm)
Adagrad解决的问题:解决不能根据参数重要性而对不同参数进行不同程度更新问题。
Adagrad参数更新原则:对低频的参数做较大的更新,对高频的参数做较小的更新。
更新公式:
其中,g为t时刻 ![]() 的梯度;
的梯度; ![]() ,
,![]() 是个对角矩阵,
是个对角矩阵,![]() 元素就是t时刻参数
元素就是t时刻参数 ![]() 的梯度平方和。
的梯度平方和。
如果是普通的SGD,那么 ![]() 在每一时刻的梯度更新公式为:
在每一时刻的梯度更新公式为:
![]() ,超参数
,超参数 ![]() 选取0.01 。
选取0.01 。
优点:减少了学习率的手动调节。
缺点:分母会不断积累,导致学习率会收缩并最终变得很小。
1.6 Adadelta
Adadelta解决的问题:解决Adagrad分母不断积累,导致学习率收缩变得非常小的问题。
Adadelta参数更新原则:和Adagrad相比,就是分母的![]() 换成了过去的梯度平方的衰减平均值,指数衰减平均值。
换成了过去的梯度平方的衰减平均值,指数衰减平均值。
这个分母相当于梯度的均方根(root mean squared,RMS),在数据统计分析中,将所有值平方求和,求其均值,再开平方,就得到均方根值,所以可以用RMS简写:
其中,E的计算公式如下, t时刻的依赖于前一时刻的平均和当前的梯度:
![]()
此外,还将学习率 ![]() 换成了
换成了![]() ,这样甚至都不需要提前设定学习率,更新公式为:
,这样甚至都不需要提前设定学习率,更新公式为:
![]() ,超参数
,超参数 ![]() 一般设定为0.9 。
一般设定为0.9 。
优点:减少了学习率的手动调节。
1.7 RMSprop
RMSprop解决的问题:RMSProp和Adadelta 都是为了解决Adagrad学习率急剧下降问题。
参数更新原则:RMSprop与Adadelta第一种形式相同:使用的是指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动,允许使用一个较大的学习率 ![]() 。
。
更新公式:
![]()
1.8 Adam(Adaptive Moment Estimation)
Adam解决的问题:这个算法是另一种计算每个参数的自适应学习率的方法。
Adam参数更新原则:相当于RMSprop + Momentum。除了像Adadelt 和RMSprop一样存储了过去梯度的平方 ![]() 的指数衰减平均值,也像Momentum一样保持了过去梯度
的指数衰减平均值,也像Momentum一样保持了过去梯度 ![]() 的指数衰减平均值:
的指数衰减平均值:
![]()
![]()
梯度更新公式:
2. LSTM里面有哪些门,为什么用这些门?
- 遗忘门:将细胞状态中的信息选择性遗忘。
- 输入门:将新的信息选择性的记录到细胞状态中。
- 输出门:当前细胞的信息保存到隐层中。
3.LSTM里面为什么有些激活函数用sigmoid,有些用tanh?
- sigmoid用在LSTM的三个门里,作用在前一个状态和输出上,主要功能是让神经元对过去输入和前一个状态的信息选择性输入,它的输出范围是(0,1),0是丢弃,1是保留;
- tanh是用在后一个状态和输出上,是对数据的处理。它的输出范围是(-1,1),功能是对哪些输出信息放大,对哪些输出信息缩小。
4. Bert中的位置向量作用是什么?有哪些生成方式?
1.位置向量的作用是表示每个单词token 距离目标单词的远近,每个token 的位置向量表示形式可以是one-hot形式,将它们合起来就是一个随机矩阵;也可以说随机id形式。
2.论文中Bert的位置向量是通过余弦函数生成,位置向量的维度和word embedding维度相同都是512维,其中位置向量的前一半通过正弦生成,后一半(后面256的长度)是通过余弦生成的。
part 2.
1. 浅copy和深copy的概念
在Python中对象的赋值其实就是对象的引用。当创建一个对象,并把它赋值给另外一个对象时,Python并没有拷贝这个对象,只是拷贝了这个对象的引用。
浅copy:拷贝了最外围的对象本身,内部的元素只是拷贝了一个引用;也就是把对象复制一遍,但是对象中引用的其他对象并不复制。比如,对于嵌套数组的浅拷贝,仅仅是拷贝外围数组元素对象,内部数组对象并不拷贝,仅拷贝引用。
深copy:外围和内部元素都进行拷贝对象本身,而不是引用。
# ---拷贝---
alist=[1, 2, 3, ['a', 'b']]
b=alist
print( b)
[1, 2, 3, ['a', 'b']]
alist.append(5)
print (alist)
print(b)
[1, 2, 3, ['a', 'b'], 5]
[1, 2, 3, ['a', 'b'], 5]
#---浅拷贝---没有拷贝子对象,所以原始数据改变,子对象会改变
# 总的来说就是,浅拷贝之后,仅仅子对象与原始数据有关系
import copy
alist=[1, 2, 3, ['a', 'b'], 5]
c=copy.copy(alist)
alist.append(5)
print(alist,c)
#输出
[1, 2, 3, ['a', 'b'], 5]
[1, 2, 3, ['a', 'b']]
alist[3].append('ccc')
print(alist,c)
#输出
[1, 2, 3, ['a', 'b', 'cccc'], 5]
[1, 2, 3, ['a', 'b', 'cccc']] 里面的子对象被改变了
# ---深拷贝---包含对象里面自对象的拷贝,所以原始对象的改变并不会造成深拷贝里面任何子元素的改变
# 总的来说就是,深拷贝之后,与原始数据已经没有关系了
[1, 2, 3, ['a', 'b'], 5]
d=copy.deepcopy(alist)
alist.append(5)
print(alist,d)
#输出
[1, 2, 3, ['a', 'b'], 5]
[1, 2, 3, ['a', 'b']]始终没有改变
alist[3].append('ccc')
print(alist,d)
#输出:
[1, 2, 3, ['a', 'b', 'ccccc'], 5]
[1, 2, 3, ['a', 'b']] 始终没有改变
2. Python中的self关键字
在Python中规定,函数的第一个参数是实例对象本身,并且约定俗成,把其名字写成self。作用类似于Java中的this关键字,表达当前类的对象,可以调用当前类的属性和方法。
3. Python中类的继承
面向对象编程的一个主要功能是继承。继承指的是,它可以使用现有类的所有功能,并在无需重写编写现有类的情况下对这些功能进行扩展。
通过继承创建的类称为子类或派生类,被继承的类称为基类或者父类,继承的过程就是从一般到特殊的过程。在某些面向对象语言中,一个子类可以继承多个基类,但一般情况下一个子类只能有一个基类。
继承的实现方式有两种:实现继承和接口继承:
- 实现继承指的是使用基类的属性和方法而无需额外编码的能力。
- 接口继承指的是仅使用属性和方法的名称,但是子类必须提供实现的能力(子类重构父类方法)。
4. 完全二叉树的概念
二叉树:树中每个节点最多有两个子节点
二叉搜索树:对于树中任何节点,如果其左子节点不为空,那么该节点的value值永远>=其左子节点;如果其右子节点不为空,那么该节点值永远<=其右子节点值。
满二叉树:树中除了叶子节点外,每个节点有2个子节点。
完全二叉树:在满足满二叉树的性质后,最后一层的叶子节点均需在最左边
完美二叉树:满足完全二叉树的性质,树的叶子节点均在最后一层。
5. 单链表与顺序表的区别
顺序表和链表是非常基本的数据结构,它们被统称为线性表,顺序表和链表是线性表的不同存储结构。
顺序表的特点是:
- 长度固定,必须在分配内存之前固定数组的长度;
- 存储空间连续,即允许元素的随机访问;
- 存储密度大,内存中存储的全部是数据元素;、
- 要访问特定元素,可以使用索引访问;
- 要想在顺序表插入或删除一个元素,都涉及到之后所有元素的移动。
而单链表是只包含指向下一个节点的指针,只能单向遍历,它的特点是:
- 长度不固定,可以任意增删;
- 存储空间不连续,数据元素之间使用指针相连,每个数据元素只能访问周围的一个元素(区别于双链表);
- 存储密度小,因为每个数据元素,都需要额外存储一个指向下一个元素的指针;
- 要访问特定元素,只能从链表头开始,遍历到该元素(顺序表只用索引查找即可)
- 在特定元素之后插入或删除元素,不需要移动其他元素。
6. 给出二叉树的前序遍历(preorder)和中序遍历(inorder),重建该二叉树:
思路:使用递归,递归的出口就是inorder为空;首先从preorder中找到根节点,然后在inorder中找到根节点的索引index;在 inorder中,index之前的左子树的节点,后面就是右子树的节点
class Solution:
def buildTree(self,preorder,inorder):
if not inorder:return None
root=TreeNode(preorder.pop(0))
index=inorder.index(root.val)
root.left=self.buildTree(preorder,inorder[:index])
root.right=self.buildTree(preorder,inorder[index+1:])
return root7.反转一个链表,并返回头结点
class Solution:
def reverseList(self, head):
if not head or not head.next:return None
prev=None
cur=head
while cur:
tmp=cur.next
cur.next=prev
prev=cur
cur=tmp
return prev
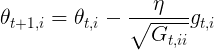
![\large \Delta \theta_t=- {\eta \over{ \sqrt{E[g^2]_t} +\epsilon }}g_{t.}](http://img.e-com-net.com/image/info8/24bbe31b84604f77aedfde517661d670.gif)
![\large \Delta \theta_t=- {{RMS[\Delta \theta]} \over {RMS[g]_t}} g_{t.}](http://img.e-com-net.com/image/info8/84d4a5d8a43d47d99f849c499850fd44.gif)
![\large \theta_{t+1} =\theta_t -{\eta \over {\sqrt{E[g^2_t] + \epsilon } }}g_{t.}](http://img.e-com-net.com/image/info8/3deff4dc82174df08b5dfe97c48db0a9.gif)