C++算法篇 贪心算法

1、接水问题  NOIP2010普及组

题目描述

学校里有一个水房，水房里一共装有m个龙头可供同学们打开水，每个龙头每秒钟的供水量相等，均为1。

现在有n名同学准备接水，他们的初始接水顺序已经确定。将这些同学按接水顺序从 1到n编号，i号同学的接水量为 wi​。接水开始时，1到m 号同学各占一个水龙头，并同时打开水龙头接水。当其中某名同学jj完成其接水量要求wj​后，下一名排队等候接水的同学 k马上接替 j同学的位置开始接水。这个换人的过程是瞬间完成的，且没有任何水的浪费。即j 同学第 x 秒结束时完成接水，则k 同学第 x+1 秒立刻开始接水。若当前接水人数 n不足 m，则只有 n个龙头供水，其它m−n个龙头关闭。

现在给出 n 名同学的接水量，按照上述接水规则，问所有同学都接完水需要多少秒。

输入格式

第 1行2 个整数 n 和 m，用一个空格隔开，分别表示接水人数和龙头个数。

第 2 行 n 个整数w1​,w2​,…,wn​，每两个整数之间用一个空格隔开，wi​表示ii号同学的接水量。

输出格式

1个整数，表示接水所需的总时间。

输入输出样例

输入 

5 3 
4 4 1 2 1 

输出

4

输入

8 4 
23 71 87 32 70 93 80 76 

输出

163

说明/提示

【输入输出样例 1 说明】

第 1 秒，3人接水。第 1秒结束时，1,2,3号同学每人的已接水量为 1,3号同学接完水，4号同学接替 3 号同学开始接水。

第 2 秒，3人接水。第2 秒结束时，1,2号同学每人的已接水量为 2,4号同学的已接水量为1。

第 3 秒，3人接水。第3 秒结束时，1,2 号同学每人的已接水量为 3,4 号同学的已接水量为2。4 号同学接完水，5 号同学接替4号同学开始接水

第4秒，3人接水。第 4秒结束时，1,2 号同学每人的已接水量为 4,5号同学的已接水量为1。1,2,5 号同学接完水，即所有人完成接水的总接水时间为 4 秒。

【数据范围】

1≤n≤10000,1≤m≤100 且m≤n；

1≤wi​≤100。

 

2、纪念品分组  NOIP2007普及组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品， 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。
你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。

输入描述:

第 1 行包括一个整数 w，为每组纪念品价格之和的上限。
第 2 行为一个整数n，表示购来的纪念品的总件数。
第 3 ~ n+2 行每行包含一个正整数 pi ( 5 ≤ pi ≤ w ) ，表示所对应纪念品的价格。

输出描述:

包含一个整数，即最少的分组数目。

示例1

输入

100
9
90
20
20
30
50
60
70
80
90

输出

6

备注:

50%的数据满足：1 ≤ n ≤ 15
100%的数据满足：1 ≤ n ≤ 30000, 80 ≤ w ≤ 200

 

3、积木大赛  NOIP2013提高组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为 n 的大厦，大厦可以看成由n块宽度为1的积木组成，第i块积木的最终高度需要是 hi 。

在搭建开始之前，没有任何积木（可以看成 n 块高度为 0 的积木）。接下来每次操作，小朋友们可以选择一段连续区间 [l, r] ，然后将第第 L 块到第 R 块之间（含第 L 块和第 R 块）所有积木的高度分别增加 1 。

小 M 是个聪明的小朋友，她很快想出了建造大厦的最佳策略，使得建造所需的操作次数最少。但她不是一个勤于动手的孩子，所以想请你帮忙实现这个策略，并求出最少的操作次数。

输入描述:

包含两行，第一行包含一个整数 n ，表示大厦的宽度。

第二行包含 n 个整数，第i个整数为 hi

输出描述:

建造所需的最少操作数。

示例1

输入

5
2 3 4 1 2

输出

5

说明

其中一种可行的最佳方案，依次选择[1,5] [1,3] [2,3] [3,3] [5,5]

备注:

对于 30% 的数据，有 1 ≤ n ≤ 10 ；
对于 70% 的数据，有 1 ≤ n ≤ 1000 ；
对于 100% 的数据，有 1 ≤ n ≤ 100000,0 ≤ hi≤ 10000 。

 

4、铺设道路  NOIP2013  提高组

题目描述

春春是一名道路工程师，负责铺设一条长度为 n 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n块首尾相连的区域，一开始，第 i 块区域下陷的深度为  di​ 。

春春每天可以选择一段连续区间 [L,R] ，填充这段区间中的每块区域，让其下陷深度减少  1。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为  0 。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 0 。

输入格式

输入文件包含两行，第一行包含一个整数  n，表示道路的长度。 第二行包含  n 个整数，相邻两数间用一个空格隔开，第  i 个整数为  di​ 。

输出格式

输出文件仅包含一个整数，即最少需要多少天才能完成任务。

输入输出样例

输入  

6   
4 3 2 5 3 5 

输出  

9

说明/提示

【样例解释】

一种可行的最佳方案是，依次选择：  [1,6]、 [1,6]、[1,2]、[1,1]、[4,6]、[4,4]、[4,4]、[6,6]、[6,6]。

【数据规模与约定】

对于  30% 的数据， 1≤n≤10 ；
对于  70% 的数据， 1≤n≤1000 ；
对于  100% 的数据，1≤n≤100000,   0≤di​≤10000 。

 

5、均分纸牌   NOIP2002  提高组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 131072K，其他语言262144K
64bit IO Format: %lld

题目描述

有N堆纸牌，编号分别为1，2，…， N。每堆上有若干张，但纸牌总数必为N的倍数。可以在任一堆上取若于张纸牌，然后移动。
移牌规则为：在编号为1堆上取的纸牌，只能移到编号为2的堆上；在编号为N的堆上取的纸牌，只能移到编号为N-1的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如 N=4，4堆纸牌数分别为：

①　9　②　8　③　17　④　6
移动3次可达到目的：
从③取4张牌放到 ④ （9 8 13 10） -> 从③取3张牌放到 ②（9 11 10 10）-> 从②取1张牌放到①（10 10 10 10）。

输入描述:

输入格式：
N（N堆纸牌，1<=N<=100）
A1 A2 … An （N 堆纸牌，每堆纸牌初始数，l<=Ai<=10000）

输出描述:

输出格式：
所有堆均达到相等时的最少移动次数。

示例1

输入

4
9 8 17 6

输出

3

 

 

6、导弹拦截   NOIP1999普及组

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是≤50000的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

1行，若干个整数（个数≤100000）

输出格式

2行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入输出样例

输入

389 207 155 300 299 170 158 65

输出 

6
2

说明/提示

为了让大家更好地测试n方算法，本题开启spj，n方100分，nlogn200分

每点两问，按问给分

 

7、三国游戏

题目描述

小涵很喜欢电脑游戏，这些天他正在玩一个叫做《三国》的游戏。

在游戏中，小涵和计算机各执一方，组建各自的军队进行对战。游戏中共有 N 位武将（N为偶数且不小于4），任意两个武将之间有一个“默契值”，表示若此两位武将作为一对组合作战时，该组合的威力有多大。游戏开始前，所有武将都是自由的（称为自由武将，一旦某个自由武将被选中作为某方军队的一员，那么他就不再是自由武将了），换句话说，所谓的自由武将不属于任何一方。

游戏开始，小涵和计算机要从自由武将中挑选武将组成自己的军队，规则如下：小涵先从自由武将中选出一个加入自己的军队，然后计算机也从自由武将中选出一个加入计算机方的军队。接下来一直按照“小涵→计算机→小涵→……”的顺序选择武将，直到所有的武将被双方均分完。然后，程序自动从双方军队中各挑出一对默契值最高的武将组合代表自己的军队进行二对二比武，拥有更高默契值的一对武将组合获胜，表示两军交战，拥有获胜武将组合的一方获胜。

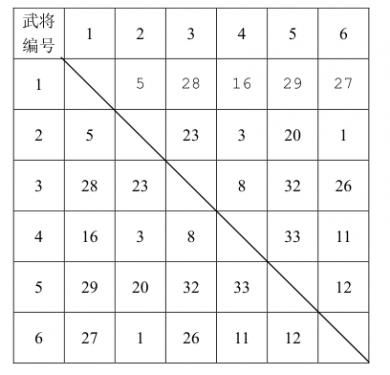
已知计算机一方选择武将的原则是尽量破坏对手下一步将形成的最强组合，它采取的具体策略如下：任何时刻，轮到计算机挑选时，它会尝试将对手军队中的每个武将与当前每个自由武将进行一一配对，找出所有配对中默契值最高的那对武将组合，并将该组合中的自由武将选入自己的军队。 下面举例说明计算机的选将策略，例如，游戏中一共有6个武将，他们相互之间的默契值如下表所示：

双方选将过程如下所示：

小涵想知道，如果计算机在一局游戏中始终坚持上面这个策略，那么自己有没有可能必胜？如果有，在所有可能的胜利结局中，自己那对用于比武的武将组合的默契值最大是多少？

假设整个游戏过程中，对战双方任何时候均能看到自由武将队中的武将和对方军队的武将。为了简化问题，保证对于不同的武将组合，其默契值均不相同。

输入格式

共 N 行。

第一行为一个偶数 N，表示武将的个数。

第 2行到第 N行里，第 i+1行有 Ni​个非负整数，每两个数之间用一个空格隔开，表示  i 号武将和i+1,i+2,…,N号武将之间的默契值（0≤默契值≤1,000,000,000）。

输出格式

共 1 或 2行。

若对于给定的游戏输入，存在可以让小涵获胜的选将顺序，则输出 1，并另起一行输出所有获胜的情况中，小涵最终选出的武将组合的最大默契值。如果不存在可以让小涵获胜的选将顺序，则输出  0。

输入输出样例

输入 

6 
5 28 16 29 27 
23 3 20 1 
8 32 26 
33 11 
12 

输出 

1
32

输入 

8 
42 24 10 29 27 12 58 
31 8 16 26 80 6 
25 3 36 11 5 
33 20 17 13 
15 77 9 
4 50 
19 

输出 

1
77

说明/提示

【数据范围】

对于40%的数据有 N≤10。

对于70%的数据有N≤18。

对于 100%的数据有N≤500。

 

9、守望者的逃离  NOIP2007普及组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

恶魔猎手尤迪安野心勃勃，他背叛了暗夜精灵，率领深藏在海底的娜迦族企图叛变。守望者在与尤迪安的交锋中遭遇了围杀，被困在一个荒芜的大岛上。为了杀死守望者，尤迪安开始对这个荒岛施咒，这座岛很快就会沉下去。到那时，岛上的所有人都会遇难。守望者的跑步速度为17m/s，以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术，可在1s内移动60m，不过每次使用闪烁法术都会消耗魔法值10点。守望者的魔法值恢复的速度为4点/s，只有处在原地休息状态时才能恢复。
现在已知守望者的魔法初值M，他所在的初始位置与岛的出口之间的距离S，岛沉没的时间T。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛，若不能逃出，则输出守望者在剩下的时间内能走的最远距离。注意：守望者跑步、闪烁或休息活动均以秒(s)为单位，且每次活动的持续时间为整数秒。距离的单位为米(m)。

输入描述:

包括空格隔开的三个非负整数M,S,T。

输出描述:

第1行为字符串“Yes”或“No”（区分大小写），即守望者是否能逃离荒岛。
第2行包含一个整数。第一行为“Yes”（区分大小写）时表示守望者逃离荒岛的最短时间；第一行为“No”（区分大小写）时表示守望者能走的最远距离。

示例1

输入

39  2004

输出

No
197

示例2

输入

36 255 10

输出

Yes 6

备注:

30%的数据满足：1 ≤ T ≤ 10, 1 ≤ S ≤ 100
50%的数据满足：1 ≤ T ≤ 1000, 1 ≤ S ≤ 10000
100%的数据满足：1 ≤ T ≤ 300000, 0 ≤ M ≤ 1000, 1 ≤ S ≤ 108.

 

 

10、排座椅    NOIP2008普及组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 51200K，其他语言102400K
64bit IO Format: %lld

题目描述

上课的时候总有一些同学和前后左右的人交头接耳，这是令小学班主任十分头疼的一件事情。不过，班主任小雪发现了一些有趣的现象，当同学们的座次确定下来之后，只有有限的D对同学上课时会交头接耳。同学们在教室中坐成了M行N列，坐在第i行第j列的同学的位置是（i，j），为了方便同学们进出，在教室中设置了K条横向的通道，L条纵向的通道。于是，聪明的小雪想到了一个办法，或许可以减少上课时学生交头接耳的问题：她打算重新摆放桌椅，改变同学们桌椅间通道的位置，因为如果一条通道隔开了两个会交头接耳的同学，那么他们就不会交头接耳了。
请你帮忙给小雪编写一个程序，给出最好的通道划分方案。在该方案下，上课时交头接耳的学生对数最少。

输入描述:

第一行，有5各用空格隔开的整数，分别是M，N，K，L，D（2 ≤ N，M ≤ 1000，0 ≤ K < M，0 ≤ L < N，D ≤ 2000）。
接下来D行，每行有4个用空格隔开的整数，第i行的4个整数Xi，Yi，Pi，Qi，表示坐在位置(Xi,Yi)与(Pi,Qi)的两个同学会交头接耳（输入保证他们前后相邻或者左右相邻）。
输入数据保证最优方案的唯一性。

输出描述:

第一行包含K个整数，a1a2……aK，表示第a1行和a1+1行之间、第a2行和第a2+1行之间、…、第aK行和第aK+1行之间要开辟通道，其中ai < ai+1，每两个整数之间用空格隔开（行尾没有空格）。
第二行包含L个整数，b1b2……bk，表示第b1列和b1+1列之间、第b2列和第b2+1列之间、…、第bL列和第bL+1列之间要开辟通道，其中bi< bi+1，每两个整数之间用空格隔开（行尾没有空格）。

示例1

输入

4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4

输出

2
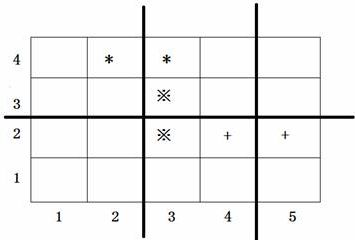
2 4

说明

上图中用符号*、※、+ 标出了3对会交头接耳的学生的位置，图中3条粗线的位置表示通道，图示的通道划分方案是唯一的最佳方案。

 

11、合并果子  NOIP2004提高组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 131072K，其他语言262144K
64bit IO Format: %lld
题目描述

    在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

    每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

    因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

输入描述:

输入包括两行，第一行是一个整数n(1<＝n<=10000)，表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai(1<＝ai<=20000)是第i种果子的数目。 

输出描述:

输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于231。

示例1

输入

3
1 2 9

输出

15

备注:

对于30％的数据，保证有n<=1000：
对于50％的数据，保证有n<=5000；
对于全部的数据，保证有n<=10000。

 

12、合并果子 加强版 NOIP2004提高组 

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 (n−1) 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为   1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有  3 堆果子，数目依次为  1, 2, 9。可以先将  1、 2 堆合并，新堆数目为  3，耗费体力为  3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为  12，耗费体力为  12。所以多多总共耗费体力为 3+12=15。可以证明  15 为最小的体力耗费值。

输入格式

输入的第一行是一个整数  n，代表果子的堆数。
输入的第二行有  n 个用空格隔开的整数，第  i 个整数代表第 i 堆果子的个数  ai​。

输出格式

输出一行一个整数，表示最小耗费的体力值。

输入输出样例

输入 

3 
1 2 9 

输出 

15

说明/提示

【数据规模与约定】

本题采用多测试点捆绑测试，共有四个子任务。

• Subtask 1（10 points）： 1≤n≤8。
• Subtask 2（20 points）： 1≤n≤10^3。
• Subtask 3（30 points）： 1≤n≤10^5。
• Subtask 4（40 points）： 1≤n≤10^7。

对于全部的测试点，保证  1≤ai​≤10^5。

【提示】

• 请注意常数因子对程序效率造成的影响。
• 请使用类型合适的变量来存储本题的结果。
• 本题输入规模较大，请注意数据读入对程序效率造成的影响。

 

13、推销员

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

阿明是一名推销员，他奉命到螺丝街推销他们公司的产品。螺丝街是一条死胡同，出口与入口是同一个，街道的一侧是围墙，另一侧是住户。螺丝街一共有N家住户，第i家住户到入口的距离为Si米。由于同一栋房子里可以有多家住户，所以可能有多家住户与入口的距离相等。阿明会从入口进入，依次向螺丝街的X家住户推销产品，然后再原路走出去。

阿明每走1米就会积累1点疲劳值，向第i家住户推销产品会积累Ai点疲劳值。阿明是工作狂，他想知道，对于不同的X，在不走多余的路的前提下，他最多可以积累多少点疲劳值。

输入描述:

第一行有一个正整数N，表示螺丝街住户的数量。

接下来的一行有N个正整数，其中第i个整数Si表示第i家住户到入口的距离。数据保证S1≤S2≤…≤Sn<108。

接下来的一行有N个正整数，其中第i个整数Ai表示向第i户住户推销产品会积累的疲劳值。数据保证Ai<103。

输出描述:

输出N行，每行一个正整数，第i行整数表示当X=i时，阿明最多积累的疲劳值。

示例1

输入

5
1 2 3 4 5
1 2 3 4 5

输出

15
19
22
24
25

说明

X=1: 向住户5推销，往返走路的疲劳值为5+5，推销的疲劳值为5，总疲劳值为15。
X=2: 向住户4、5推销，往返走路的疲劳值为5+5，推销的疲劳值为4+5，总疲劳值为5+5+4+5=19。
X=3: 向住户3、4、5推销，往返走路的疲劳值为5+5，推销的疲劳值3+4+5，总疲劳值为5+5+3+4+5=22。
X=4: 向住户2、3、4、5推销，往返走路的疲劳值为5+5，推销的疲劳值2+3+4+5，总疲劳值5+5+2+3+4+5=24。
X=5: 向住户1、2、3、4、5推销，往返走路的疲劳值为5+5，推销的疲劳值1+2+3+4+5，总疲劳值5+5+1+2+3+4+5=25。

示例2

输入

5
1 2 2 4 5
5 4 3 4 1

输出

12
17
21
24
27

说明

X=1：向住户4推销，往返走路的疲劳值为4+4，推销的疲劳值为4，总疲劳值4+4+4=12。
X=2：向住户1、4推销，往返走路的疲劳值为4+4，推销的疲劳值为5+4，总疲劳值4+4+5+4=17。
X=3：向住户1、2、4推销，往返走路的疲劳值为4+4，推销的疲劳值为5+4+4，总疲劳值4+4+5+4+4=21。
X=4：向住户1、2、3、4推销，往返走路的疲劳值为4+4，推销的疲劳值为5+4+3+4，总疲劳值4+4+5+4+3+4=24。或者向住户1、2、4、5推销，往返走路的疲劳值为5+5，推销的疲劳值为5+4+4+1，总疲劳值5+5+5+4+4+1=24。
X=5：向住户1、2、3、4、5推销，往返走路的疲劳值为5+5，推销的疲劳值为5+4+3+4+1，总疲劳值5+5+5+4+3+4+1=27。

备注:

对于20%的数据，1≤N≤20；
对于40%的数据，1≤N≤100；
对于60%的数据，1≤N≤1000；
对于100%的数据，1≤N≤100000。

14、国王游戏   NOIP 2012 提高组 第一天 第二题

题目描述

恰逢 H 国国庆，国王邀请 n  位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这 n  位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。

输入格式

第一行包含一个整数 n ，表示大臣的人数。

第二行包含两个整数 a 和 b，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来 n 行，每行包含两个整数a  和  b，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

输出格式

一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

输入输出样例

输入

3 
1 1 
2 3 
7 4 
4 6 

输出 

2

说明/提示

【输入输出样例说明】

按1 、2 、3  这样排列队伍，获得奖赏最多的大臣所获得金币数为  2；

按 1 、3 、2 这样排列队伍，获得奖赏最多的大臣所获得金币数为 2；

按  2、 1、3 这样排列队伍，获得奖赏最多的大臣所获得金币数为 2 ；

按2 、3 、1 这样排列队伍，获得奖赏最多的大臣所获得金币数为 9；

按 3 、1 、 2这样排列队伍，获得奖赏最多的大臣所获得金币数为 2；

按3 、2 、1  这样排列队伍，获得奖赏最多的大臣所获得金币数为  9。

因此，奖赏最多的大臣最少获得  2个金币，答案输出  2。

【数据范围】

对于 20%的数据，有  1≤n≤10,0

对于 40%的数据，有 1≤n≤20,0

对于 60%的数据，有  1≤n≤100；

对于 60%的数据，保证答案不超过 10^9  ；

对于 100%的数据，有  1≤n≤1,000,0

 

15、旅行家的预算  NOIP 1999 提高组

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 131072K，其他语言262144K
64bit IO Format: %lld

题目描述

一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市（假设出发时油箱是空的）。给定两个城市之间的距离D1、汽车油箱的容量C（以升为单位）、每升汽油能行驶的距离D2、出发点每升汽油价格P和沿途油站数N（N可以为零），油站i离出发点的距离Di、每升汽油价格Pi（i=1，2，…，N）。

计算结果四舍五入至小数点后两位。如果无法到达目的地，则输出“No Solution”。

输入描述:

第一行：D1，C，D2，P，N。

接下来有N行。

第i+1行，两个数字，油站i离出发点的距离Di和每升汽油价格Pi。

输出描述:

所需最小费用，计算结果四舍五入至小数点后两位。如果无法到达目的地，则输出“No Solution”。

示例1

输入

275.6 11.9 27.4 2.8 2
102.0 2.9
220.0 2.2

输出

26.95

备注:

N≤6,其余数字≤500

 

16、扑克牌

题目描述

你有 n 种牌，第i种牌的数目为 ci​。另外有一种特殊的牌：joker，它的数目是 m。你可以用每种牌各一张来组成一套牌，也可以用一张 joker 和除了某一种牌以外的其他牌各一张组成 1套牌。比如，当 n=3时，一共有 4 种合法的套牌：{1,2,3}，{J,2,3}，{1,J,3}，{1,2,J}。给出 n，m 和 ci​，你的任务是组成尽量多的套牌。每张牌最多只能用在一副套牌里（可以有牌不使用）。

输入格式

第一行包含两个整数 n，m，即牌的种数和 joker 的个数。

第二行包含 n 个整数ci​，即每种牌的张数。

输出格式

输出仅一个整数，即最多组成的套牌数目。

输入输出样例

输入 

3 4
1 2 3

输出 

3

说明/提示

样例说明

输入数据表明：一共有 1 个 1，2个 2，3 个 3，4 个 joker。最多可以组成三副套牌：{1,J,3}，{J,2,3}，{J,2,3}，joker 还剩一个，其余牌全部用完。

数据范围

对于 50% 的数据 ，2≤n≤5，0≤m≤10^6，0≤ci​≤200。

对于100% 的数据，2≤n≤50， 0≤m,  ci​≤5×10^8。