漫步数学分析十三——路径连通

第二个重要的主题是连通性，我们直观上知道想应用连通性到哪种集合上，然而，我们的直观在判断更复杂的集合时可能会失效，例如如果 R2 中的集合为 {(x,sin1/x)|x>0}∪{(0,y)|y∈[−1,1]} ，那么它是连通的吗？如图 ??? 所示，现在我们想用严格的定义来形式化这个概念。

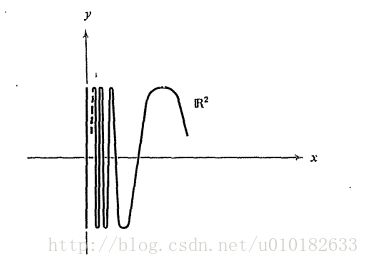
图1

事实上，有两个不同但彼此相互联系的连通概念，其中更加直观且实用的是路径连通(path-connectedness)，所以我们先从它入手，首先我们需要定义连接两点的曲线是什么。

定义2 连接 Rn 中两点 x,y 的连续路径是一个映射： φ:[a,b]→Rn ，它满足 φ(a)=x,φ(b)=y 且 φ 是连续的，这里 x,y 可能相等，也可能不相等 b≥a ，在随后的文章中我们会详细的研究连续映射，但是目前，如果对于 [a,b] 中收敛到某个值 t∈[a,b] 的每个序列 tk ，满足

(tk→t)⇒(φ(tk)→φ(t))

那么我们就说 φ 是连续的。(直观上来看，连续路径就是该路径上没有断点或跳跃点)如果对于所有的 t∈[a,b] ， φ(t)∈A ，那么我们说路径 φ 位于集合 A 中，如图 ??? 所示。

如果集合 A 中的任意两点被一条位于 A 中的连续路径连接起来，那么我们就成集合 A 是路径连续的(path-connected)。

例如，图 ??? 中的区域 A 是路径连通的，另一个路径连通集是区间 [0,1] 本身。为了证明这个结论，令 x,y∈[0,1] 并且定义 φ:[0,1]→R,φ(t)=(y−x)t+x ，这是连接 x,y 的路径，它位于 A=[0,1] 中。

利用上面路径连通的定义，有一个事实是图 ??? 中的集合不是路径连通的，虽然这个事实得证明比较繁琐。许多时候判断集合是否是路径连通的非常容易，只需要看任何两点是否可以由位于集合中的曲线连接起来，并且几何直观也很明显。连通的第二个概念不太好直接判断，但是非常有用我们会在下一篇文章中给出。

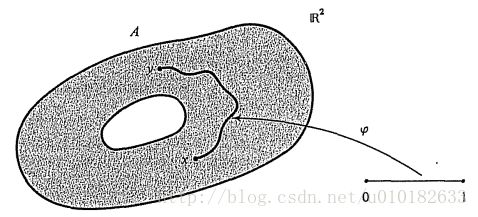
图2

例1： 下面那些集合是路径连通的？

(a) [0,3]
(b) [1,2]∪[3,4]
(c) {(x,y)∈R2|0<x≤1}
(d) {(x,y)∈R2|0<x2+y2≤1}

解： 只有(b)不是路径连通的，从图 ??? 可以很明显的看出来。

例2： 路径连通必须是闭的吗？或者开的？

解： 不需要。[0,1],(0,1),[0,1)都是路径连通的。

例3： 令 φ:[0,1]→R3 是一个连续路径，并且 ℓ=φ([0,1]) ，说明 ℓ 是路径连续的。

解： 这在直观上很明显，因为我们可以用 φ 本身取连接 ℓ 中的任意两点。更准确的说，如果 x=φ(a),y=φ(b) ，其中 0≤a≤b≤1 ，令 c:[a,b]→R3,c(t)=φ(t) ，那么 c 是连接 x,y 的路径且位于 ℓ 中。

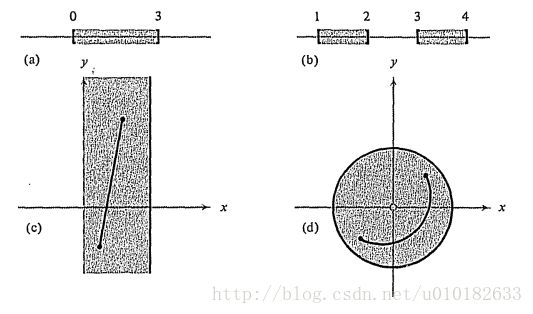
图3