数据预处理，降维，特征提取，聚类

数据预处理，降维，特征提取，聚类

数据预处理，使用StandardScaler进行数据的预处理

# 导入numpy
import numpy 
# 导入绘图工具
import matplotlib.pyplot as plt
%matplotlib inline
# 导入数据集生成工具
from sklearn.datasets import make_blobs
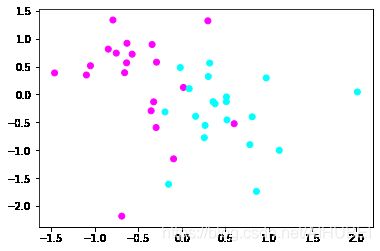
X, y = make_blobs(n_samples=40, centers=2, random_state=50, cluster_std=2)
# 使用散点图绘制数据
plt.scatter(X[:,0], X[:,1], c = y, cmap = plt.cm.cool)
plt.show()

样本数为40，分类centers为2，随机状态random_state为50，标准差cluster_std为2的数据。

使用sklearn的preprocessing模块对这个手工生成的数据集进行处理

# 导入StandardScaler
from sklearn.preprocessing import StandardScaler
# 使用StandardScaler进行数据预处理
X_1 = StandardScaler().fit_transform(X)
# 使用散点图绘制经过数据预处理的数据点
plt.scatter(X_1[:,0], X_1[:,1], c = y, cmap=plt.cm.cool)
# 显示图像
plt.show()

似乎没有什么变化，但是这里的$x$和$y$轴发生了变化，现在的数据所有的特征1的数值都在-2到3之间，特征2的数值都在-3到2之间。因为StandardScaler的原理就是，把所有的数据的特征值转化为;均值为零，方差为一的状态。这样一来就可以确保数据的大小都是一致的，更有利于模型的训练。

使用MinMaxScaler进行数据预处理

# 导入MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
# 使用MinMaxScaler进行数据预处理
X_2 = MinMaxScaler().fit_transform(X)
# 绘制散点图
plt.scatter(X_2[:,0],X_2[:,1],c=y,cmap=plt.cm.cool)
plt.show()

这样一来，所有的数据每个特征值都被转换到0和1之间。这会使得模型的训练速度加快，同时准确率也会得以提高。

使用RobustScaler进行数据预处理

# 导入RobustScaler
from sklearn.preprocessing import RobustScaler
# 使用RobustScaler进行数据预处理
X_3 = RobustScaler().fit_transform(X)
# 绘制散点图
plt.scatter(X_3[:,0], X_3[:,1], c=y, cmap=plt.cm.cool)
plt.show()

这种方法和StandarScaler比较近似，但是他使用的是中位数和四分位数。他会直接把一些异常值剔除，有点类似于“去掉一个最高分，去掉一个最低分”

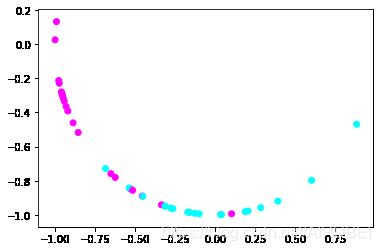
使用Normalizer进行数据预处理

# 导入Normalizer
from sklearn.preprocessing import Normalizer
# 使用Normalizer进行数据预处理
X_4 = Normalizer().fit_transform(X)
# 绘制散点图
plt.scatter(X_4[:,0], X_4[:,1], c=y, cmap=plt.cm.cool)
plt.show()

Normalizer方法讲数据或者说所有样本的特征向量转化为欧几里得距离为1.也就是把数据的分布变成一个半径为1的圆， 或者是一个球。通常在，我们只想保留数据的特征向量的方向，而忽略其数值的时候使用。

使用scale函数，对单个类似数组的数据集执行操作

import sklearn.preprocessing
import numpy as np
X_train = np.array([[1, -1, 2],
                   [2, 0, 0],
                   [0, 1, -1]])
X_scaled = sklearn.preprocessing.scale(X_train)
plt.scatter(X_train[:2,:],X_train[1:3,:])
plt.show()

X_scaled

array([[ 0.        , -1.22474487,  1.33630621],
       [ 1.22474487,  0.        , -0.26726124],
       [-1.22474487,  1.22474487, -1.06904497]])

plt.scatter(X_scaled[:2,:],X_scaled[1:3,:])
plt.show()

print("均值:",X_scaled.mean(axis = 0))
print("单位方差:",X_scaled.std(axis = 0))

均值: [0. 0. 0.]
单位方差: [1. 1. 1.]

标度数据的均值和单位方差为零

使用MaxAbsScaler进行数据预处理

# 导入MaxAbsScaler
from sklearn.preprocessing import MaxAbsScaler
# 使用Normalizer进行数据预处理
X_5 = MaxAbsScaler().fit_transform(X)
# 绘制散点图
plt.scatter(X_5[:,0], X_5[:,1], c=y, cmap=plt.cm.cool)
plt.show()

通过其最大绝对值缩放每个特征。分别缩放和转换每个特征，以使训练集中每个特征的最大绝对值为1.0。它不会移动/居中数据，因此不会破坏任何稀疏性。
该缩放器也可以应用于稀疏CSR或CSC矩阵。

print(X_5.mean())
print(X_5.std())

-0.3163704548637977
0.306489301692821

处理类别特征 使用OrdinalEncoder

通常，特征不是连续值而是类别型的。比如一个人的特征，这样的特征可以有效的编码为整数。使用OrdinalEncoder,实现讲类别特征编码到：(0 to n_categories -1)

# 导入OrdinalEncoder
from sklearn.preprocessing import OrdinalEncoder
# 使用OrdinalEncoder编码数据
Y = [['male', 'from US', 'uses Safari'],
     ['female', 'from Europe', 'uses Firefox']]
Y_ordinal = OrdinalEncoder().fit_transform(Y)
Y_ordinal

array([[1., 1., 1.],
       [0., 0., 0.]])

但是，此类整数表示不能直接与所有scikit-learn估计器一起使用，因为它们期望连续输入，并且会将类别解释为有序的，这通常是不希望的（即，浏览器集是任意定序的）。

处理类别特征 使用独热码OneHotEncoder

# 导入OneHotEncoder
from sklearn.preprocessing import OneHotEncoder
# 使用OneHotEncoder处理数据
Y = [['male', 'from US', 'uses Safari'],
     ['female', 'from Europe', 'uses Firefox']]
Y_OneHot = OneHotEncoder().fit_transform(Y)
Y_OneHot

<2x6 sparse matrix of type ''
	with 6 stored elements in Compressed Sparse Row format>

Y_OneHot.toarray()

array([[0., 1., 0., 1., 0., 1.],
       [1., 0., 1., 0., 1., 0.]])

OneHotEncoder().fit(Y)

OneHotEncoder(categories='auto', drop=None, dtype=,
              handle_unknown='error', sparse=True)

OneHotEncoder().categories

'auto'

它将带有n_categories可能值的每个分类特征 转换为n_categories二进制特征，其中一个为1，所有其他为0

# 可以使用参数明确指定categories
genders = ['female', 'male']
locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
# 特征
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
X_fit = OneHotEncoder(categories=[genders, locations, browsers]).fit_transform([['female', 'from Asia', 'uses Chrome']]).toarray()
X_fit

array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

X_fit = OneHotEncoder(categories=[genders, locations, browsers]).fit_transform(X).toarray()
X_fit

array([[0., 1., 0., 0., 0., 1., 0., 0., 0., 1.],
       [1., 0., 0., 0., 1., 0., 0., 1., 0., 0.]])

如果训练数据有可能缺少分类特征，则通常最好指定handle_unknown='ignore’而不是categories如上所述手动设置。如果 handle_unknown='ignore’指定且在转换过程中遇到未知类别，则不会引发错误，但是此功能生成的一键编码列将全为零（handle_unknown='ignore’仅一键编码支持）：

# 数据/特征
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
X_fit = OneHotEncoder(handle_unknown='ignore').fit(X)
X_fit

OneHotEncoder(categories='auto', drop=None, dtype=,
              handle_unknown='ignore', sparse=True)

X_fit = OneHotEncoder(handle_unknown='ignore').fit_transform(X).toarray()
X_fit

array([[0., 1., 0., 1., 0., 1.],
       [1., 0., 1., 0., 1., 0.]])

使用Binarizer进行特征二值化，特征二值化是阈值化数字特征以获得布尔值的过程

# 在文本处理中使用二值化特征很常见，即使在实践归一化数据的表现要好一些。
X = [[ 1., -1.,  2.],
    [ 2.,  0.,  0.],
    [ 0.,  1., -1.]]
# 导入Binarizer
from sklearn.preprocessing import Binarizer
# 使用Binarizer处理数据
X_Bina = Binarizer().fit_transform(X)
X_Bina

array([[1., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.]])

# 可以调整二值化器的阈值 将数据进行二值化，threshold表示大于阈值的数据为1,小于阈值的数据为0
# 使用Binarizer处理数据
X_Bina = Binarizer(threshold=1).fit_transform(X)
X_Bina

array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 0., 0.]])

缺失值的估算

由于各种原因，许多现实世界的数据集包含缺失值，通常将其编码为空白，NaN或其他占位符。但是，此类数据集与scikit-learn估计器不兼容，后者假定数组中的所有值都是数字，并且都具有并具有含义。使用不完整数据集的基本策略是丢弃包含缺失值的整个行和/或列。但是，这是以丢失有价值的数据为代价的（即使数据不完整）。更好的策略是估算缺失值，即从数据的已知部分推断出缺失值。参见 插补的通用术语表和API元素条目。

单变量特征插补

该SimpleImputer课程提供了估算缺失值的基本策略。可以使用提供的恒定值或使用缺失值所在各列的统计信息（平均值，中位数或最频繁）来估算缺失值。此类还允许使用不同的缺失值编码。

# 使用np.nan编码为缺失值，使用各列的均值来替换缺失值
import numpy as np
from sklearn.impute import SimpleImputer
imp = SimpleImputer(missing_values=np.nan, strategy='mean')
imp.fit([[1,2], [np.nan, 3], [7,6]])

SimpleImputer(add_indicator=False, copy=True, fill_value=None,
              missing_values=nan, strategy='mean', verbose=0)

X = [[np.nan, 2],[6, np.nan],[7, 6]]
print(imp.transform(X))

[[4.         2.        ]
 [6.         3.66666667]
 [7.         6.        ]]

X = [[np.nan, 2],[6, np.nan],[7, 6]]
X_impute = SimpleImputer().fit_transform(X)
X_impute

array([[6.5, 2. ],
       [6. , 4. ],
       [7. , 6. ]])

SimpleImputer同时也支持稀疏矩阵

import scipy.sparse as sp
X = sp.csc_matrix([[1,2],[0,-1],[8,4]])
X

<3x2 sparse matrix of type ''
	with 5 stored elements in Compressed Sparse Column format>

X_sparse = SimpleImputer(missing_values = -1, strategy='mean').fit_transform(X)
X_sparse

<3x2 sparse matrix of type ''
	with 5 stored elements in Compressed Sparse Column format>

print(X_sparse.toarray())

[[1. 2.]
 [0. 3.]
 [8. 4.]]

SimpleImputer同时也可以用于处理分类型的数据

import pandas as pd
df = pd.DataFrame([["a", "x"],
                  [np.nan, "y"],
                  ["a", np.nan],
                  ["b", "y"]], dtype="category")

# 使用出现频率最高的数据进行填补空值
df_IMputer = SimpleImputer(strategy="most_frequent").fit_transform(df)
print(df_IMputer)

[['a' 'x']
 ['a' 'y']
 ['a' 'y']
 ['b' 'y']]

多元特征插补

import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

imp = IterativeImputer(max_iter=10, random_state=0)
imp.fit([[1, 2], [3, 6], [4, 8], [np.nan, 3], [7, np.nan]])

X_test = [[np.nan, 2], [6, np.nan], [np.nan, 6]]
# the model learns that the second feature is double the first
print(np.round(imp.transform(X_test)))

[[ 1.  2.]
 [ 6. 12.]
 [ 3.  6.]]

# 显示的导入enable_iterative_imputer后
# 再从sklearn.impute 导入IterativeImputer
# from sklearn.experimental import enable_iterative_imputer  
# from sklearn.impute import IterativeImputer

# from sklearn.ensemble import RandomForestRegressor
# import pandas as pd

# # 载入数据
# titanic = pd.read_csv("titanic.csv")
# titanic = titanic.loc[:, ['Pclass', 'Age', 'SibSp', 'Parch', 'Fare']]

# # 使用随机森林估计器
# imp = IterativeImputer(RandomForestRegressor(), max_iter=10, random_state=0)
# titanic = pd.DataFrame(imp.fit_transform(titanic), columns=titanic.columns)

实例1

# 导入红酒数据集
from sklearn.datasets import load_wine
# 导入MLP神经网络
from sklearn.neural_network import MLPClassifier
# 导入数据集拆分工具
from sklearn.model_selection import train_test_split
# 建立训练集和测试集
wine = load_wine()
X_train, X_test, y_train, y_test = train_test_split(wine.data, wine.target, random_state=62)
# 打印数据集
print(X_train.shape, X_test.shape)

(133, 13) (45, 13)

import warnings
warnings.filterwarnings("ignore")

# 设定MLP神经网络的参数
mlp = MLPClassifier(hidden_layer_sizes=[100,100],max_iter=400,random_state=62)
# 使用MLP拟合数据
mlp.fit(X_train, y_train)
print("未经处理的数据，模型得分为:{:.2f}".format(mlp.score(X_test, y_test)))

未经处理的数据，模型得分为:0.93

设定MLP的隐藏层为2， 每一层100各节点，最大迭代次数400，同时指定random_state,从而保证，重复使用该模型的时候，训练的结果是一致的。

# 使用MinMaxScaler进行数据预处理
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_pp = scaler.transform(X_train)
X_test_pp = scaler.transform(X_test)
# 再次训练模型
mlp.fit(X_train_pp, y_train)
# 打印模型表现
print("经处理的数据，模型得分为:{:.2f}".format(mlp.score(X_test_pp, y_test)))

经处理的数据，模型得分为:1.00

数据降维-----主成分分析

# 导入红酒数据集
from sklearn.preprocessing import StandardScaler
# 对红酒数据集进行预处理
scaler = StandardScaler()
X = wine.data
y = wine.target
# 处理之后的数据
X_scaled = scaler.fit_transform(X)
print(X_scaled.shape)

(178, 13)

现在的数据集中，样本数量为178，特征数量为13.

# 导入PCA
from sklearn.decomposition import PCA
# 设置主成份数量为6
pca = PCA(n_components=2)
pca.fit(X_scaled)
X_pca = pca.transform(X_scaled)
# 打印主成分提取之后的数据形态
print(X_pca.shape)

(178, 2)

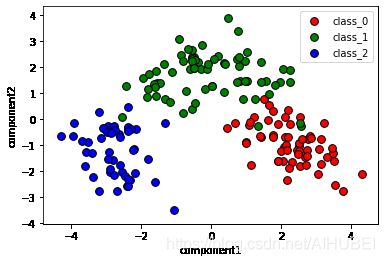
# 把三个分类中的主成分提取出来
X0 = X_pca[wine.target==0]
X1 = X_pca[wine.target==1]
X2 = X_pca[wine.target==2]

# 散点图
plt.scatter(X0[:,0], X0[:,1],c='r', s=60,edgecolor='k')
plt.scatter(X1[:,0], X1[:,1],c='g', s=60,edgecolor='k')
plt.scatter(X2[:,0], X2[:,1],c='b', s=60,edgecolor='k')

# 设置图注
plt.legend(wine.target_names,loc='best')
plt.xlabel('component1')
plt.ylabel('component2')
# 显示
plt.show()

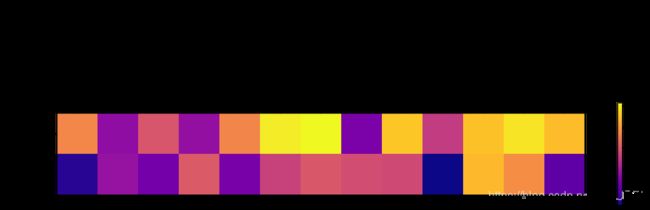
原始特征与PCA主成分之间的关系

# 使用主成分绘制热力图
plt.matshow(pca.components_, cmap='plasma')
# 纵轴为主成分数量
plt.yticks([0,1],["component1","component2"])
plt.colorbar()
# 横轴为原始特征数量
plt.xticks(range(len(wine.feature_names)), wine.feature_names, rotation=60, ha='left')
# 显示图像
plt.show()

特征提取

特征提取，是构造一个新的特征空间，并将原始特征投影在新的空间中得到新的表示。以线性投影为例，令$\mathbf{X}\in {\mathcal{R}}^D$为原始特征空间，${\mathbf{X}}^{\prime }\in {\mathcal{R}}^K$是经过线性投影后得到的在新空间中的特征向量，如下:
$${\mathbf{X}}^{\prime }=\mathbf{W}\mathbf{X}$$
其中，$\mathbf{W}\in {\mathcal{R}}^{KxD}$为映射矩阵。

PCA主成分分析用于特征提取

# 导入数据集获取工具
from sklearn.datasets import fetch_lfw_people
# 载入人脸数据集
faces = fetch_lfw_people(min_faces_per_person=20, resize=0.8)
# 将照片打印出来
fig, axes = plt.subplots(3,4,figsize=(12,9),subplot_kw={'xticks':(), 'yticks':()})
for target, image,ax in zip(faces.target, faces.images, axes.ravel()):
    ax.imshow(image, cmap=plt.cm.gray)
ax.set_title(faces.target_names[target])
plt.show()

# 导入神经网络
from sklearn.neural_network import MLPClassifier
X_train, X_test, y_train, y_test = train_test_split(faces.data/255, faces.target, random_state=60)
mlp=MLPClassifier(hidden_layer_sizes=[100,100],random_state=62,max_iter=500)
mlp.fit(X_train, y_train)
print("模型识别准确率:{:.2f}".format(mlp.score(X_test, y_test)))

模型识别准确率:0.59

使用白化功能，白化的目的就是：降低冗余性。白化的过程会让样本之间的相关性降低，且所有特征具有相同的方差

# 使用白化功能处理数据
pca = PCA(whiten=True, n_components=0.9, random_state=60).fit(X_train)
X_train_whiten = pca.transform(X_train)
X_test_whiten = pca.transform(X_test)
X_train_whiten.shape

(1740, 101)

# 使用白化之后的数据训练神经网络
mlp.fit(X_train_whiten, y_train)
mlp.score(X_test_whiten, y_test)

0.6327586206896552

K均值聚类

from sklearn.datasets import make_blobs
# 生成分类数为1的数据集
blobs = make_blobs(random_state=1, centers=1)
X_blobs = blobs[0]
plt.scatter(X_blobs[:,0],X_blobs[:,1],c='r',edgecolor='k')
plt.show()

使用K均值进行聚类

# 导入KMeans
from sklearn.cluster import KMeans
# 设定为3类
kmeans = KMeans(n_clusters=3)
# 拟合数据
kmeans.fit(X_blobs)

x_min, x_max = X_blobs[:,0].min()-0.5, X_blobs[:,0].max()+0.5
y_min, y_max = X_blobs[:,1].min()-0.5, X_blobs[:,1].max()+0.5

xx, yy = np.meshgrid(np.arange(x_min, x_max, .02),np.arange(y_min, y_max, .02))

z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)

plt.figure(1)
plt.clf()

plt.imshow(z, interpolation='nearest', extent=(xx.min(), xx.max(), yy.min(),yy.max()),cmap=plt.cm.summer, aspect='auto', origin='lower')

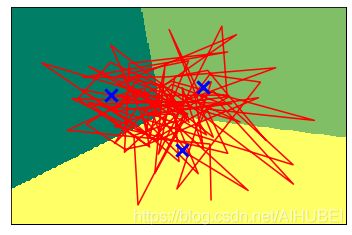
plt.plot(X_blobs[:, 0], X_blobs[:, 1], 'r', markersize=5)

# 使用蓝色的❌代表据类的中心
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:,0], centroids[:,1],
           marker = 'x',s = 150, linewidth=3,
           color = 'b', zorder=10)

plt.xlim(x_min,x_max)
plt.ylim(y_min,y_max)

plt.xticks(())
plt.yticks(())

plt.show()

# 打印Kmeans进行聚类的标签

print("K均值的聚类标签:\n{}".format(kmeans.labels_))

K均值的聚类标签:
[2 2 0 1 1 1 2 2 0 1 2 1 2 0 2 1 1 2 0 0 1 0 2 2 2 2 1 2 2 2 0 0 2 2 1 0 1
 0 2 0 1 2 0 0 1 1 1 2 0 2 0 2 1 0 1 1 0 1 1 2 1 0 1 2 0 1 0 0 2 1 1 2 1 1
 1 2 1 2 2 0 1 0 1 1 0 2 1 2 0 0 1 2 0 0 1 1 2 1 1 2]

凝聚聚类算法

# 导入dendrogram和ward工具
from scipy.cluster.hierarchy import dendrogram, ward
# 使用连线的方式进行可视化
linkage = ward(X_blobs)
dendrogram(linkage)

ax = plt.gca()

plt.xlabel("sample index")
plt.ylabel("Cluster distance")

plt.show()