前言
学习面向对象这门课程的后的第一单元作业,主线是多项式求导,三次作业层层推进,由单一的幂函数求导,到幂函数和三角函数的复合求导,最后再到两种函数的嵌套求导,由两个类到重构后的十几个类,我逐渐对面向对象的思想有了更深一步的理解,对结构化的设计也有了更加深刻的体会。
第一次作业
作业要求
实现仅含幂函数和常数的多项式求导,数据长度上限1000,性能上要求结果越短越好(即化简到最简),保证输入数据合法。
实现简述
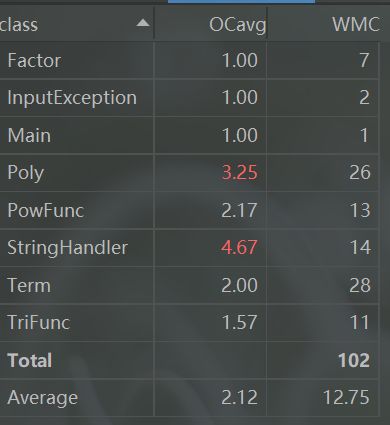
完成本次作业时,由于扩展意识不足,采取了仅为解决当前问题的设计模式,包含两个类Poly和PolyComputer,其中Poly类用一个HashMap来存储多项式每一项的系数和指数,使用BigInteger来管理系数和指数,用PolyComputer类读入字符串并进行处理,并在其中直接对求导结果进行输出,以下是我的类图分析
优缺点评价
-
优点
-
由于保证输入数据合法,在dispose处理字符串时先去掉空格并对先连的正负号进行合并,使得在parsePoly中利用正则表达式解析字符串更加简便
-
在用addTerm增加项时利用DegExist判断当前指数的项是否存在,存在就直接合并,做到了及时合并同类项
-
在printDeva输出时对系数和指数为0、±1时进行了特判,使输出结果达到较简的形式
-
-
缺点
-
在输出时的特判情况较多, 易出错
-
直接对多项式进行求导,没有存储求导结果,使得printDeva与其它模块的耦合性过强,代码质量低
-
由于前期对字符串进行处理后再进行正则判断,无法适应后面需要判断格式的改变
-
未对函数设置专门类,导致代码在遇到多种函数复合求导时需要重构,扩展性低
-
bug分析
本次作业中,由于我在判断输出是失误,导致>1时才输出指数,因为这一个失误下的大bug,在强测及互测阶段我被hack得很惨。当然我也进行了深刻的反思,由于第一次作业对规则还不是特别熟悉,自己在课下并没有做好充分的测试,才导致了这一bug苟过中测残留到强测及互测阶段。
在对别人的代码进行测试的过程中,我一般是构造边缘数据进行测试,如系数及指数为±1、0,连续几项相同指数需要合并,常数单一项等的情况,然后再读别人的代码进行针对性测试。最后,也成功几次hack到了别人。
第二次作业
作业要求
在第二次作业中,增加了三角函数的求导及f(x)*g(x)的复合求导形式,但三角函数因子只能为sin(x)和cos(x),同时,也要求对输入数据进行格式判断。
实现简述
在实现本次作业过程中,由于上一次代码扩展性太差,且考虑到下次作业会更加复杂,我选择了及时重构。重构时的思路主要分为以下三个方面:
1、结构化层次关系的设计
首先,我定义了Factor类,设置系数和指数属性,在里面定义了一些因子共有的特征及加和乘的运算,然后使幂函数PowFunc和三角函数TriFunc 继承自Factor类,在每个子类中重写derivation()和toString()方法,在三角函数内设type属性存储三角函数类型。
然后,考虑到本次作业的特征,每项最多由幂函数*正弦函数*余弦函数的格式组成,故在Term类仅设置三个因子对象做为属性,并对无参数的构造方法初始化为系数为1,指数为0的形式,同时,为了将每项系数合为一起,我将幂函数的系数默认为项的系数,在每一项被加入到多项式时利用combineCoef()方法将三个函数的系数合并。
最后,将原来的Poly类内由存每项的系数和指数,改为存多个Term的容器,并且在addTerm()时利用isCoefZero()及时删去了零项。
总之,在对象的创建上,我整体实现了由factor→term→poly的层次结构。
关于求导方面,我利用三层结构的迭代求导,在Term类内的derivation()方法中根据f(x)*g(x)的求导规则进行特殊书写。
2、输入数据的格式判断及解析
对于Wrong Format!判断,我自定义了InputException()的例外,并在其中设置printError()方法,在检测到非法格式时抛出例外。在Main类中进行try-catch的捕捉。
由于上次作业我先对表达式进行处理,导致无法判断输入数据格式,在本次作业中,我将原来的PolyComputer类改为StringHandler类,进行输入数据的判断和处理,并在正则表达式中补入了空格,先根据正则表达式检测数据格式,然后用dispose()方法对表达式进行处理,最后以项为单位解析表达式,存入一个Poly对象中。
3、关于优化
这次的作业如果利用各种三角函数的公式,其实有很多点可以进行优化,但是很多时候实现并不容易,且容易引发很多未知bug,况且很多优化规则的实例出现概率很小,故我最后只在以下三个方面进行了优化。
-
sin2(x)+cos2(x)=1
-
同类项合并
-
x**2→x*x
最后,我重构后的代码结构类图分析如下:
其中,StringHandler的循环复杂度较高,但因为涉及到字符串的解析,所以我认为是无法避免的。
优缺点评价
-
优点
-
结构层次较为清楚,有一定的可扩展性
-
各类功能简单,不易出现bug
-
实现了简单的优化
-
-
缺点
-
对Term类的属性处理不当,导致后面在增加多中因子时需要重构,改为存储Factor的容器
-
在Poly中进行优化时涉及到多个类的方法调用,耦合度较高
-
在StringHandler处理字符串时,生成项判断可以利用工厂方法来进行解耦,也会使思路更加清晰
-
bug分析
由于吸取了上一次的经验,之前进行了自我测试,并写了自动化测试工具进行测试,在强测及互测阶段,我的程序并没有被hack到,但我也知道它可能在某个神奇的地方仍存在bug
与此同时,在测试别人代码时,我偷懒使用了自动化测试工具, 并且由于当时在忙一些其它的事情,我没有时间去分析完每个人的代码,自己构造的一些测试点也没有hack到别人,最后自动化测试也不争气,我体会了唯一一个和平的互刀环节。
第三次作业
作业要求
本次作业主要增加了三角函数的嵌套求导,并增加了表达式因子
实现简述
1、结构层次关系的设计
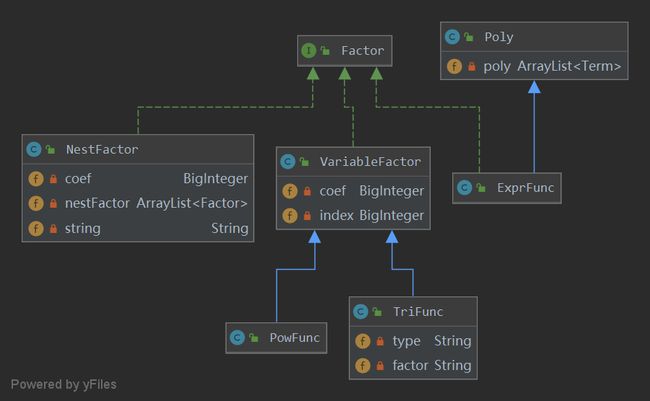
由于增加了表达式因子和嵌套的三角函数,我增加了NestFactor和ExprFunc两类,其中ExprFunc继承自Poly类,将原来的Factor父类改为存储变量因子的VariableFactor,并使所有的因子实现Factor接口,实现求导、加乘等一系列因子的基本操作。
在处理嵌套因子时,由于嵌套的求导规则是对每层进行求导并相乘,在这里,为了防止爆栈,我在NestFactor用了一个Factor的容器,从外向内存储嵌套每层因子,求导时只需对容器的每一项进行求导,对于三角函数括号内的部分在TriFunc中定义factor字符串直接进行存储,在输出时代替原来x的位置即可
具体的UML类图如下:
2、输入数据的格式判断及解析
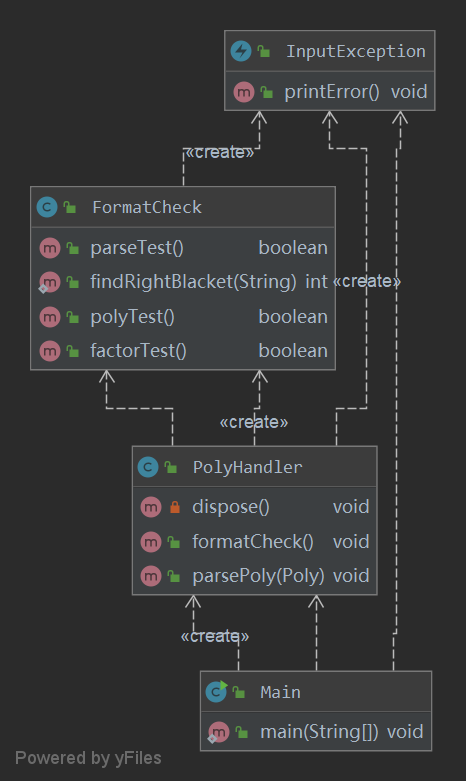
在输入数据的格式判断,由于此次为含递归的正则表达式,不能简单用正则表达式直接判断,在此,我新建了一个FormatCheck类,对输入表达式进行递归判断,并专门写一个findRightBlacket()的静态方法,返回与当前字符串最左侧括号所匹配的右括号位置。
在解析表达式时,我新建了一个PolyHandler类,将表达式以项为单位传入Term中,循环填充一个Poly类的对象,同时,为了减少类之间的耦合度,我将格式检查也在这里进行。具体的关系如下图:
在解析表达式时,吸取上一次的经验,我新建了FactorFactory的工厂类,把解析出的因子表达式传入生成相应类型的Factor对象
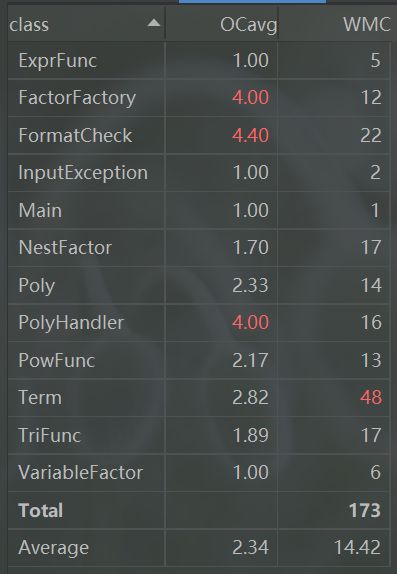
在下面类度量中,可以发现在,仍是在含表达式的解析的类循环复杂度比较高
3、关于优化
-
实现了部分同类的因子和项之间的合并
-
在NestFactor中,通过重写的toString()对嵌套因子内部的字符串进行循环替换,简化了含前导0、符号多余以及因子之间可合并的地方
-
x**2→x*x
优缺点评价
-
优点
-
表达式的解析分为几部分在类的内部执行,减少了表达式解析的循环深度
-
迭代求导部分思路比较清楚
-
嵌套因子的处理较为简便
-
-
缺点
-
由于三角函数可被归为ExprFunc和TriFunc两类,同类项合并时不好判断
-
由于表达式因子的存在,使得因子求导的返回必须是Poly类对象,对于VariableFactor类,其实返回Factor类就够了,但还需要把他们一步步转成Poly类,觉得较为冗余,但也没有好的办法解决
-
在对求导结果进行复合时,需要分类处理,不能做到很好的归一化,否则会出现神奇的bug,感觉有点麻烦,应该还有解决办法
-
bug分析
这次作业太过复杂了,果然最后出现了一些很神奇的边缘bug,虽然很好改,但我被hack得很惨
-
在表达式因子求导得到Term类对象后,我将它toString()的结果传入了Term中进行新的一项的解析,但由于我将x**2转化成了x*x,会导致传入sin(x*x)类不合法因子,而我并未对此类因子进行解析,所以最终会出现RuntimeError
-
在由于优化, 输出时可能会有sin(x*x)类不合法输出格式的因子
-
由于我在TriFunc类里的toString()方法内直接选择对factor为0的因子输出为0,导致有cos(0)时会出现错误
在测别人的bug时,我针对sin(0)**0,cos(0)等类型的易错点设置了测试样例,果然也hack到了一波别人,同时也测试了多层括号嵌套、连续符号判断等情况
总结