第一单元是关于表达式求导,共涉及三次迭代作业,在难度,复杂度,鲁棒性等均有升级。
第一次作业
分析
第一次作业难度较小,且不会出现WRONG FORMAT,因此可以大胆处理。先直接去掉空格来使输入变得简单。且由于因子只会出现幂函数和常数,因此我考虑用Hashmap将指数和系数对应,进行运算和化简。
层次分析
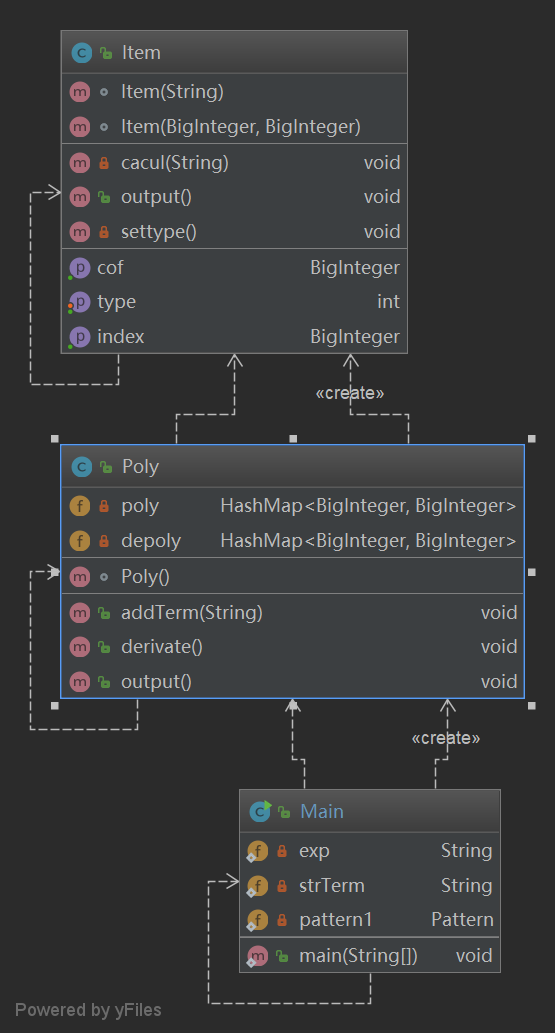
UML类图:
第一次作业为了后面的拓展性和架构,用了三个类,一个是主类Main,一个是整体的表达式Poly,一个是是表达式每项Item,层层递进,既符合表达式项的架构,也为后面的迭代预留了空间。
代码复杂度分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| task.Item.Item(BigInteger,BigInteger) | 1 | 1 | 1 |
| task.Item.Item(String) | 1 | 1 | 1 |
| task.Item.cacul(String) | 3 | 6 | 6 |
| task.Item.getCof() | 1 | 1 | 1 |
| task.Item.getIndex() | 1 | 1 | 1 |
| task.Item.getType() | 1 | 1 | 1 |
| task.Item.output() | 1 | 16 | 16 |
| task.Item.setType(int) | 1 | 1 | 1 |
| task.Item.settype() | 1 | 3 | 4 |
| task.Main.main(String[]) | 1 | 2 | 2 |
| task.Poly.Poly() | 1 | 1 | 1 |
| task.Poly.addTerm(String) | 3 | 3 | 3 |
| task.Poly.derivate() | 1 | 3 | 3 |
| task.Poly.output() | 4 | 6 | 7 |
整体来说,耦合度不高,但也存在局部较高的地方,比如task.Item.output(),这是因为这个在我设计是用来处理最后的Poly类,并将其转成字符串来将其输出,与其他方法耦合度较高。
反思
我优化是通过合并同类项并将正数输出到第一项,效果较好,同时在本次作业中架构比较简单,因此bug并不多。但还有许多地方需要注意,比如多个运算符,还有指数为0等情况,特别是许多同学在优化过程中,忘记最后如果结果为0需要特判输出。
但在我程序架构中,没有将Func抽象出来,直接用幂函数的指数和系数代表因子,可以说有点投机取巧,因此后面作业拓展遇到了不小麻烦,只好重构。
第二次作业
分析
第二次作业难度大了许多,而且开始出现WRONG FORMAT,因此需要特判。我判断WRONG FORMAT是通过枚举错误情况,但由于第二次作业不会出现空格错误,因此可以先直接去掉空格来使输入变得简单。
在第一次作业由于因子只会出现幂函数和常数,用Hashmap将指数和系数对应,进行运算和化简。但第二次作业中已经有了sin cos三角函数,因此用Hashmap难度变大了许多,因此在以后的作业中,我采用了Arraylist 来进行数据存储。同时函数已经有许多种了,因此我将函数抽象出来,设计了Func抽象类,然后设计了Sin Cos Power类继承,其他架构与第一次相似。
在分项时主要采用正则表达式,由于第二次作业因子形式比较固定,因此这种方法效果较好,但在第三次作业中这种方法很难发挥神威了,需要替换。
同时在互测过程中借鉴了同组同学代码的优点,将一些符号替换,来使处理复杂度降低。
层次分析
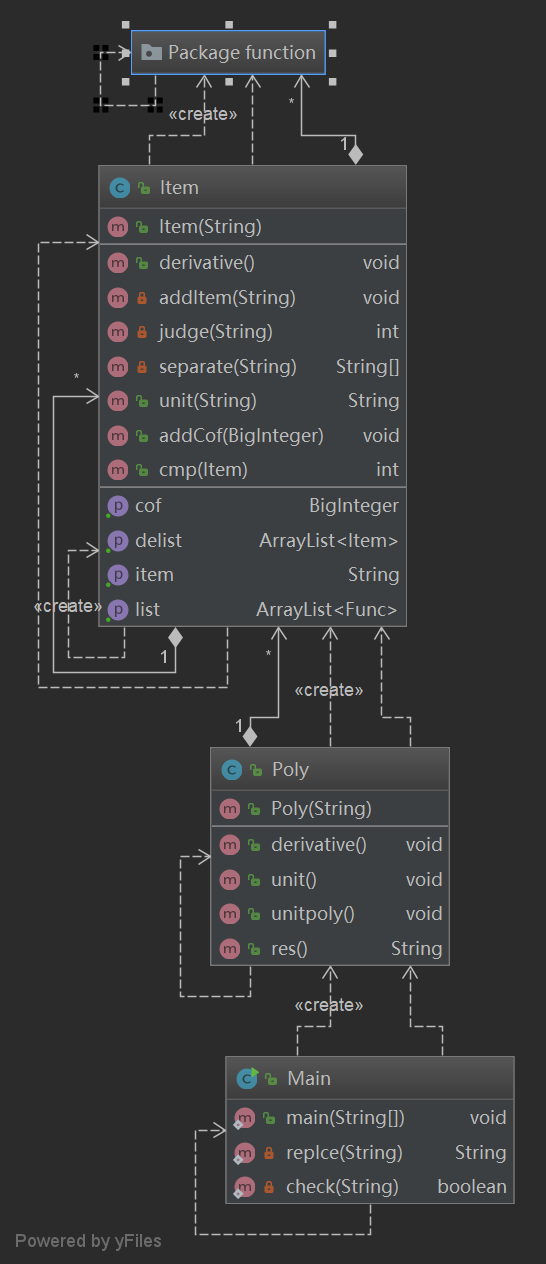
UML类图:
第二次作业同第一次,依旧设置了主类Main,其作用是读取字符串,简单处理后(比如替换和查错),并将其送进Poly类,由Poly类的方法将其转换成一个多项式,然后Poly类进行分项,将分后的项传入Item类构造项,Item类再引用抽象类Func的子类方法实现化简运算等。
求导时,只需调用Poly类的求导方法,这样就可以一直从上到下调用求导方法来实现目的。
代码复杂度分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| task.Item.Item(String) | 1 | 1 | 1 |
| task.Item.addCof(BigInteger) | 1 | 1 | 1 |
| task.Item.addItem(String) | 1 | 9 | 9 |
| task.Item.cmp(Item) | 4 | 3 | 4 |
| task.Item.derivative() | 4 | 3 | 4 |
| task.Item.getCof() | 1 | 1 | 1 |
| task.Item.getDelist() | 1 | 1 | 1 |
| task.Item.getItem() | 1 | 2 | 2 |
| task.Item.getList() | 1 | 1 | 1 |
| task.Item.judge(String) | 4 | 5 | 5 |
| task.Item.separate(String) | 1 | 2 | 2 |
| task.Item.unit(String) | 5 | 5 | 10 |
| task.Main.check(String) | 10 | 3 | 10 |
| task.Main.main(String[]) | 2 | 2 | 2 |
| task.Main.replce(String) | 1 | 2 | 3 |
| task.Poly.Poly(String) | 3 | 2 | 3 |
| task.Poly.derivative() | 1 | 3 | 3 |
| task.Poly.res() | 1 | 4 | 6 |
| task.Poly.unit() | 3 | 3 | 4 |
| task.Poly.unitpoly() | 6 | 9 | 11 |
| task.function.Cos.Cos() | 1 | 1 | 1 |
| task.function.Cos.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Cos.derivative() | 2 | 3 | 3 |
| task.function.Cos.getCof() | 1 | 1 | 1 |
| task.function.Cos.getDeFunc() | 1 | 1 | 1 |
| task.function.Cos.getFunc() | 3 | 4 | 4 |
| task.function.Cos.getIndex() | 1 | 1 | 1 |
| task.function.Cos.getType() | 1 | 1 | 1 |
| task.function.Cos.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Cos.setFunc(String) | 4 | 5 | 5 |
| task.function.Power.Power() | 1 | 1 | 1 |
| task.function.Power.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Power.derivative() | 2 | 3 | 3 |
| task.function.Power.getCof() | 1 | 1 | 1 |
| task.function.Power.getDeFunc() | 1 | 1 | 1 |
| task.function.Power.getFunc() | 3 | 4 | 4 |
| task.function.Power.getIndex() | 1 | 1 | 1 |
| task.function.Power.getType() | 1 | 1 | 1 |
| task.function.Power.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Power.setFunc(String) | 4 | 5 | 5 |
| task.function.Sin.Sin() | 1 | 1 | 1 |
| task.function.Sin.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Sin.derivative() | 2 | 3 | 3 |
| task.function.Sin.getCof() | 1 | 1 | 1 |
| task.function.Sin.getDeFunc() | 1 | 1 | 1 |
| task.function.Sin.getFunc() | 3 | 4 | 4 |
| task.function.Sin.getIndex() | 1 | 1 | 1 |
| task.function.Sin.getType() | 1 | 1 | 1 |
| task.function.Sin.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Sin.setFunc(String) | 4 | 5 | 5 |
由于在设计中需要从上到下的引用,因此耦合度较第一次作业高了一些,但总体情况还是较好的。
不过有些方法复杂度较高,比如task.Poly.unitpoly() task.Main.check(String)等,他们主要是用来处理字符串的,需要我程序中定义的一些静态变量,因此耦合度偏高。
反思
本次作业中WRONG FORMAT判断的不好,导致失了一些分,同时在优化过程中产生了一些不必要的bug,在互测过程中被hack出来。
在判断WF中,我采用的是枚举错误的方法,这种很难覆盖所有错误情况,因此失分也是情理之中。讨论区有许多同学提出边处理边判断的方法,符合架构,值得借鉴学习。同时在自己测试中,分为了几种情况爆破,将自己逻辑复杂度较高的部分集中爆破,测出了一些bug,并预测和查看了同组同学的代码较复杂的部分,自己的bug和再次构造的bug测了同屋的同学。
本次架构为第三次作业留了许多可以拓展的空间,这也使得第三次作业不需要重构。同时Poly Item Func类等单独处理自己需要处理的,通过引用即可,很好的体现了面向对象的思想。
第三次作业
分析
第三次作业难度又大了许多,而且由于表达式方式多变,因此会出现复杂WRONG FORMAT。我判断WRONG FORMAT是通过枚举错误情况,先判断是否是由空格引起,在判断是否是由于其他情况引起的。
在第二次作业由于sin cos三角函数中因子固定,处理难度不大,但在第三次作业中,因子嵌套,需要采用递归思想来构造。同时我仍然继承了第二次作业设计的Func抽象类,然后设计了Sin Cos Power类继承,并新加了Const Exp两个“类函数”来继承。
在分项时由于因子嵌套,很难再次采用大正则表达式直接分项。因此在第三次作业中我采取了有限状态机来进行分项。
同时在互测过程中借鉴了同组同学代码的优点,将一些符号替换,来使处理复杂度降低。
层次分析
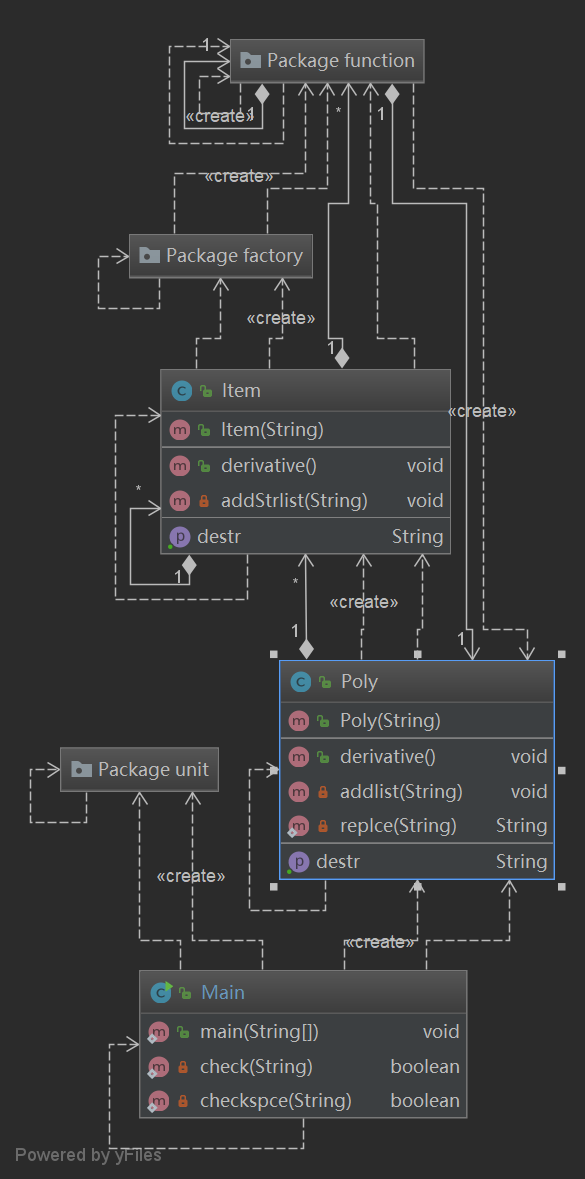
UML类图:
第三次作业架构与第二次类似,依旧设置了主类Main,其作用是读取字符串,简单处理后(比如替换和查错),并将其送进Poly类,由Poly类的方法将其转换成一个多项式,然后Poly类进行分项,将分后的项传入Item类构造项,Item类再引用抽象类Func的子类方法实现化简运算等。
求导时,只需调用Poly类的求导方法,这样就可以一直从上到下调用求导方法来实现目的。
而对于函数求导,需要借用相互引用,即Exp中引用的Poly类,来进行递归求导,最后采用字符串的形式拼接在一起输出。
代码复杂度分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| task.Item.Item(String) | 1 | 3 | 3 |
| task.Item.addStrlist(String) | 1 | 6 | 6 |
| task.Item.derivative() | 5 | 4 | 6 |
| task.Item.getDestr() | 1 | 1 | 1 |
| task.Main.check(String) | 13 | 2 | 13 |
| task.Main.checkspce(String) | 6 | 3 | 7 |
| task.Main.main(String[]) | 3 | 6 | 6 |
| task.Poly.Poly(String) | 1 | 2 | 2 |
| task.Poly.addlist(String) | 1 | 12 | 12 |
| task.Poly.derivative() | 1 | 3 | 4 |
| task.Poly.getDestr() | 1 | 1 | 1 |
| task.Poly.replce(String) | 1 | 1 | 1 |
| task.factory.Factory.check(String) | 1 | 6 | 6 |
| task.factory.Factory.getConst(String) | 1 | 1 | 1 |
| task.factory.Factory.getCos(String) | 1 | 1 | 1 |
| task.factory.Factory.getExp(String) | 1 | 1 | 1 |
| task.factory.Factory.getFunc(String) | 5 | 7 | 7 |
| task.factory.Factory.getPower(String) | 1 | 1 | 1 |
| task.factory.Factory.getSin(String) | 1 | 1 | 1 |
| task.function.Const.Const(String) | 1 | 1 | 1 |
| task.function.Const.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Const.derivative() | 1 | 1 | 1 |
| task.function.Const.getCof() | 1 | 1 | 1 |
| task.function.Const.getDeFunc() | 1 | 1 | 1 |
| task.function.Const.getFunc() | 1 | 1 | 1 |
| task.function.Const.getIndex() | 1 | 1 | 1 |
| task.function.Const.getType() | 1 | 1 | 1 |
| task.function.Const.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Const.setFunc(String) | 1 | 1 | 1 |
| task.function.Cos.Cos(String) | 1 | 1 | 1 |
| task.function.Cos.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Cos.check(String) | 5 | 1 | 5 |
| task.function.Cos.derivative() | 2 | 4 | 4 |
| task.function.Cos.getCof() | 1 | 1 | 1 |
| task.function.Cos.getDeFunc() | 1 | 1 | 1 |
| task.function.Cos.getFunc() | 1 | 1 | 1 |
| task.function.Cos.getIndex() | 1 | 1 | 1 |
| task.function.Cos.getType() | 1 | 1 | 1 |
| task.function.Cos.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Cos.setFunc(String) | 1 | 12 | 13 |
| task.function.Exp.Exp(String) | 1 | 2 | 2 |
| task.function.Exp.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Exp.derivative() | 1 | 1 | 1 |
| task.function.Exp.getCof() | 1 | 1 | 1 |
| task.function.Exp.getDeFunc() | 1 | 1 | 1 |
| task.function.Exp.getFunc() | 1 | 1 | 1 |
| task.function.Exp.getIndex() | 1 | 1 | 1 |
| task.function.Exp.getType() | 1 | 1 | 1 |
| task.function.Exp.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Exp.setFunc(String) | 1 | 1 | 1 |
| task.function.Power.Power(String) | 1 | 1 | 1 |
| task.function.Power.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Power.derivative() | 2 | 3 | 3 |
| task.function.Power.getCof() | 1 | 1 | 1 |
| task.function.Power.getDeFunc() | 1 | 1 | 1 |
| task.function.Power.getFunc() | 1 | 1 | 1 |
| task.function.Power.getIndex() | 1 | 1 | 1 |
| task.function.Power.getType() | 1 | 1 | 1 |
| task.function.Power.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Power.setFunc(String) | 2 | 3 | 4 |
| task.function.Sin.Sin(String) | 1 | 1 | 1 |
| task.function.Sin.addIndex(BigInteger) | 1 | 1 | 1 |
| task.function.Sin.check(String) | 5 | 1 | 5 |
| task.function.Sin.derivative() | 2 | 4 | 4 |
| task.function.Sin.getCof() | 1 | 1 | 1 |
| task.function.Sin.getDeFunc() | 1 | 1 | 1 |
| task.function.Sin.getFunc() | 1 | 1 | 1 |
| task.function.Sin.getIndex() | 1 | 1 | 1 |
| task.function.Sin.getType() | 1 | 1 | 1 |
| task.function.Sin.mulCof(BigInteger) | 1 | 1 | 1 |
| task.function.Sin.setFunc(String) | 1 | 12 | 13 |
| task.unit.Poly2.Poly2(String) | 1 | 1 | 1 |
| task.unit.Poly2.getRes() | 1 | 1 | 1 |
| task.unit.Poly2.replce(String) | 1 | 2 | 3 |
由于在设计中需要从上到下的引用,因此耦合度较第二次作业高了一些,但总体情况还是较好的,平均值甚至较第二次降了一些。
不过有些方法复杂度较高,比如task.Main.check(String)等,他们主要是用来处理字符串的,需要我程序中定义的一些静态变量,因此耦合度偏高。
反思
本次作业架构比较复杂,因此没有怎么优化,性能分也得的不多,在借鉴了同学分享的优秀代码后,发现搜索和贪心都是很不错的优化思路。
在判断WF中,我采用的是枚举错误的方法,这种很难覆盖所有错误情况,因此失分也是情理之中。讨论区有许多同学提出边处理边判断的方法,符合架构,值得借鉴学习。同时在自己测试中,分为了几种情况爆破,将自己逻辑复杂度较高的部分集中爆破,测出了一些bug,并预测和查看了同组同学的代码较复杂的部分,自己的bug和再次构造的bug测了同屋的同学。
本次作业是在第二次作业上拓展而来,仍然很好的体现了面向对象思想,但部分类或方法之间的耦合度较高,这仍是我需要提高的地方。
测试Bug
三次作业难度呈明显上升趋势,随着工程量增大,潜在bug数也会增大,因此测试Bug是一个很重要的部分。
我测试主要采用两种办法:
-
对自己逻辑复杂的地方进行集中爆破,这些地方很容易出现逻辑混乱的地方。
-
对边界极端情况进行单独测试,保证自己没有遗漏特殊的地方。
测试同学时也主要采用上述方法。
总结
这一单元只是这个课程的开端,我们仍需要花很多功夫去提高,去真正地理解面向对象。
同时在checkstyle等工具下,强制改掉自己不好的编程习惯。