面向对象编程 之 第一单元总结
本次单元的三次作业内容主题依据多项式求导依次展开。本文将主要围绕代码的架构设计以及规模分析,从架构设计、 程序结构分析、自动化测试以及总结感想四方面对此次作业进行阐述。
- 面向对象编程 之 第一单元总结
- 1.多项式求导架构设计分析
- 1.2.2 多项式类
- 1.3.2 三角函数多项式
- 1.3.3 带嵌套的函数多项式
- 2.错误分析
- 2.1 错误分析
- 3.自动化测试
- 3.1 基于Python的压力测试
- 3.2 互测对拍器
- 4.工厂设计模式
- 1.多项式求导架构设计分析
1.多项式求导架构设计分析
### 1.1 需求分析 第一次作业,主要是简单多项式导函数的求解。第二次作业中,表达式因子形式在第一次作业的基础上,支持标准三角函 数(sin(x)、cos(x))为底数的幂函数。第三次作业中,进一步支持求解包含简单幂函数和简单正余弦函数并存在内嵌多 项式的导函数。
### 1.2 实现方案
#### 1.2.1 输入处理
为了避开正则表达式繁琐的匹配情况,笔者采用了不带回溯的递归下降的语法分析器。递归下降分析器的构造方法非常简单
,即每一个非终结符对应一个递归函数,保证下一层可能转换成的所有情况的第一个字符不同,随后构建语法树。这也便于
我们的输入合法性判断,利用assert语句,一旦出现非法输入立马报错。经过整理后的处理BNF规则以及对应方法如下(第
三次作业,InputParser类):
//expr ::= sign? term { SIGN term }*
Expression parseExpression();
//term ::= sign? factor { MULT factor }*
Term parseTerm(Sign sign);
//firstfactor ::= sign? factor
Derivative parseFirstFactor();
//factor ::= signed_int | function | (expr)
Derivative parseFactor();
//function ::= power | tri
Derivative parseFunction();
//power ::= x ** signed_int
Factor parsePowerFunction();
//tri ::= sin(factor)** signed_int| cos(factor) ** signed_int
Factor parseTriFunction(String idenfer);
String parseIdenfer();
BigInteger parseSignedInteger();
Sign parseSign();
void parseSpace();
对应的度量分析:
| poly.InputParser.checkLegal(String) | 2.0 | 1.0 | 2.0 |
|---|---|---|---|
| poly.InputParser.checkOutOfIndex(BigInteger) | 2.0 | 1.0 | 2.0 |
| poly.InputParser.getExpression() | 1.0 | 1.0 | 1.0 |
| poly.InputParser.getSignIdenfer() | 1.0 | 1.0 | 2.0 |
| poly.InputParser.hasNext() | 1.0 | 1.0 | 1.0 |
| poly.InputParser.InputParser(String,int) | 2.0 | 1.0 | 2.0 |
| poly.InputParser.isCharacter(char) | 1.0 | 1.0 | 1.0 |
| poly.InputParser.isDigit(char) | 1.0 | 1.0 | 1.0 |
| poly.InputParser.isSign(char) | 1.0 | 1.0 | 2.0 |
| poly.InputParser.isSpace(char) | 1.0 | 1.0 | 2.0 |
| poly.InputParser.parseExpression() | 3.0 | 5.0 | 5.0 |
| poly.InputParser.parseFactor() | 3.0 | 4.0 | 4.0 |
| poly.InputParser.parseFirstFactor() | 2.0 | 3.0 | 3.0 |
| poly.InputParser.parseFunction() | 2.0 | 2.0 | 2.0 |
| poly.InputParser.parseIdenfer() | 1.0 | 3.0 | 3.0 |
| poly.InputParser.parsePowerFunction() | 1.0 | 3.0 | 3.0 |
| poly.InputParser.parseSign() | 4.0 | 4.0 | 4.0 |
| poly.InputParser.parseSignedInteger() | 2.0 | 5.0 | 5.0 |
| poly.InputParser.parseSpace() | 1.0 | 3.0 | 3.0 |
| poly.InputParser.parseTerm(Sign) | 1.0 | 4.0 | 4.0 |
| poly.InputParser.parseTriFunction(String) | 4.0 | 3.0 | 6.0 |
| poly.InputParser.peek() | 2.0 | 1.0 | 2.0 |
| poly.InputParser.poll() | 1.0 | 1.0 | 1.0 |
| poly.InputParser.selfAssert(char) | 2.0 | 2.0 | 2.0 |
| Total | 42.0 | 53.0 | 63.0 |
| Average | 1.75 | 2.2083333333333335 | 2.625 |
parseSign()方法被判定ev过高是因为由三个if,设计问题不算太大;而parseTriFunction()方法认定为ev过高是用于判
断求导类型的三个if,思考后,应该可以用多态的方法一并解决,减少逻辑分支。
1.2.2 多项式类
如图所示,第一次作业结构较为简单,以加减号为隔断依据,每项分割为新的PolyItem,整个多项式最终聚合为Expression
。
Main调用InputParser产生Expression,整体结构层次较为清晰。
| expression.Expression.addExpr(PolyItem) | 1.0 | 2.0 | 2.0 |
|---|---|---|---|
| expression.Expression.checkLegal() | 1.0 | 1.0 | 1.0 |
| expression.Expression.Expression() | 1.0 | 1.0 | 1.0 |
| expression.Expression.getDerivative() | 1.0 | 3.0 | 3.0 |
| expression.Expression.toString() | 2.0 | 5.0 | 6.0 |
| expression.PolyItem.add(PolyItem) | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.clone() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.compareTo(PolyItem) | 2.0 | 2.0 | 2.0 |
| expression.PolyItem.derive() | 2.0 | 1.0 | 2.0 |
| expression.PolyItem.equals(Object) | 2.0 | 3.0 | 3.0 |
| expression.PolyItem.equivalent(Object) | 2.0 | 2.0 | 2.0 |
| expression.PolyItem.getCoef() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.getIdx() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.hashCode() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.isConst() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.isPos() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.isZero() | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.PolyItem(BigInteger,BigInteger) | 1.0 | 1.0 | 1.0 |
| expression.PolyItem.simplifyNumber(BigInteger) | 1.0 | 2.0 | 2.0 |
| expression.PolyItem.toString() | 8.0 | 3.0 | 10.0 |
| Main.main(String[]) | 1.0 | 2.0 | 2.0 |
| parser.Function.Function(String) | 1.0 | 1.0 | 1.0 |
| parser.Function.getPresent() | 1.0 | 1.0 | 1.0 |
| Total | 60.0 | 83.0 | 101.0 |
| Average | 1.5384615384615385 | 2.128205128205128 | 2.58974358974359 |
可以看到,除了inputparser外(上述情况见1.2.1),toString类的ev过高,应该是使用了过多if语句对多种不同情况进
行了特判,造成复杂的逻辑分支。对特殊情况进行汇总,在后两次作业中有修改。
(2)第二次作业

由于本次作业较为特殊,所以采用架构与第一次作业类似,Main调用InputParser产生Expression,Factor类可以归并到
Term类。类中有四个BigInteger域,分别对应常数,幂因子的指数,正弦函数的指数和余弦函数的指数,用以保存最简式的
变量。
同时注意到,实现了Derivative接口,用于构建Expression时更容易匹配类型。此次作业中继承BasicFunction抽象类的两
个类没有实现具体接口,仅仅服务于作业的扩展性。除此之外,使用了Enum类型的Function,负责匹配因子类型,与程序
的主体耦合性较低。
| BasicFunction.BasicFunction(Function,BigInteger) | 1.0 | 1.0 | 1.0 |
|---|---|---|---|
| BasicFunction.getFunctionType() | 1.0 | 1.0 | 1.0 |
| BasicFunction.getIdx() | 1.0 | 1.0 | 1.0 |
| BasicFunction.isZero() | 1.0 | 1.0 | 1.0 |
| Expression.add(Expression) | 1.0 | 2.0 | 2.0 |
| Expression.add(SimpTerm,BigInteger) | 2.0 | 2.0 | 3.0 |
| Expression.add(Term) | 1.0 | 1.0 | 1.0 |
| Expression.clone() | 1.0 | 2.0 | 2.0 |
| Expression.compareTo(Expression) | 1.0 | 1.0 | 1.0 |
| Expression.derive() | 1.0 | 2.0 | 2.0 |
| Expression.equals(Object) | 2.0 | 2.0 | 2.0 |
| Expression.Expression() | 1.0 | 1.0 | 1.0 |
| Expression.Expression(HashMap) | 1.0 | 1.0 | 1.0 |
| Expression.Expression(Term...) | 1.0 | 2.0 | 2.0 |
| Expression.extract(Term) | 1.0 | 1.0 | 1.0 |
| Expression.hashCode() | 1.0 | 1.0 | 1.0 |
| Expression.isZero() | 1.0 | 1.0 | 1.0 |
| Expression.reduce(Expression,Term,Term,int) | 2.0 | 2.0 | 8.0 |
| Expression.reduce(HashSet,Expression,SimpTerm,SimpTerm,int) | 2.0 | 2.0 | 4.0 |
| Expression.simplify(long) | 1.0 | 5.0 | 5.0 |
| Expression.toString() | 3.0 | 6.0 | 7.0 |
| Factor.Factor() | 1.0 | 1.0 | 2.0 |
| Factor.Factor(BigInteger,BigInteger...) | 1.0 | 1.0 | 1.0 |
| Factor.multiply(Factor) | 1.0 | 2.0 | 2.0 |
| Factor.negate() | 1.0 | 1.0 | 1.0 |
| Factor.setCoef(BigInteger) | 1.0 | 1.0 | 1.0 |
| Factor.setIdx(Function,BigInteger) | 1.0 | 1.0 | 1.0 |
| Factor.toTerm() | 1.0 | 1.0 | 1.0 |
| Function.Function(String) | 1.0 | 1.0 | 1.0 |
| Function.getStr() | 1.0 | 1.0 | 1.0 |
| InputParser.checkLegal(String) | 2.0 | 1.0 | 2.0 |
| InputParser.checkOutOfIndex(BigInteger) | 2.0 | 1.0 | 2.0 |
| InputParser.getExpression() | 1.0 | 1.0 | 1.0 |
| InputParser.getSignIdenfer() | 1.0 | 1.0 | 2.0 |
| InputParser.hasNext() | 1.0 | 1.0 | 1.0 |
| InputParser.InputParser(String) | 1.0 | 1.0 | 1.0 |
| InputParser.isCharacter(char) | 1.0 | 1.0 | 1.0 |
| InputParser.isDigit(char) | 1.0 | 1.0 | 1.0 |
| InputParser.isSign(char) | 1.0 | 1.0 | 2.0 |
| InputParser.isSpace(char) | 1.0 | 1.0 | 2.0 |
| InputParser.parseExpression() | 1.0 | 4.0 | 4.0 |
| InputParser.parseFactor() | 2.0 | 3.0 | 3.0 |
| InputParser.parseFirstFactor() | 2.0 | 3.0 | 3.0 |
| InputParser.parseFunction() | 2.0 | 2.0 | 2.0 |
| InputParser.parseIdenfer() | 1.0 | 3.0 | 3.0 |
| InputParser.parsePowerFunction() | 1.0 | 3.0 | 3.0 |
| InputParser.parseSign() | 4.0 | 4.0 | 4.0 |
| InputParser.parseSignedInteger() | 2.0 | 5.0 | 5.0 |
| InputParser.parseSpace() | 1.0 | 3.0 | 3.0 |
| InputParser.parseTerm(Sign) | 1.0 | 4.0 | 4.0 |
| InputParser.parseTriFunction(String) | 1.0 | 3.0 | 3.0 |
| InputParser.peek() | 2.0 | 1.0 | 2.0 |
| InputParser.poll() | 1.0 | 1.0 | 1.0 |
| InputParser.selfAssert(char) | 2.0 | 2.0 | 2.0 |
| Main.main(String[]) | 1.0 | 2.0 | 2.0 |
| Power.derive() | 1.0 | 1.0 | 1.0 |
| Power.isZero() | 1.0 | 1.0 | 1.0 |
| Power.Power(Function,BigInteger) | 1.0 | 1.0 | 1.0 |
| SimpTerm.clone() | 1.0 | 1.0 | 1.0 |
| SimpTerm.derive() | 1.0 | 1.0 | 1.0 |
| SimpTerm.equals(Object) | 2.0 | 2.0 | 2.0 |
| SimpTerm.getCosIdx() | 1.0 | 1.0 | 1.0 |
| SimpTerm.getIdx() | 1.0 | 1.0 | 1.0 |
| SimpTerm.getPowrIdx() | 1.0 | 1.0 | 1.0 |
| SimpTerm.getSinIdx() | 1.0 | 1.0 | 1.0 |
| SimpTerm.hashCode() | 1.0 | 1.0 | 1.0 |
| SimpTerm.isZero() | 1.0 | 1.0 | 1.0 |
| SimpTerm.SimpTerm() | 1.0 | 1.0 | 2.0 |
| SimpTerm.SimpTerm(BigInteger...) | 1.0 | 1.0 | 1.0 |
| Term.add(Derivative) | 1.0 | 1.0 | 1.0 |
| Term.compareTo(Term) | 1.0 | 1.0 | 1.0 |
| Term.derive() | 1.0 | 4.0 | 4.0 |
| Term.equals(Object) | 2.0 | 3.0 | 3.0 |
| Term.equivalent(Term) | 1.0 | 1.0 | 1.0 |
| Term.getCoef() | 1.0 | 1.0 | 1.0 |
| Term.getCosIdx() | 1.0 | 1.0 | 1.0 |
| Term.getIdx() | 1.0 | 1.0 | 1.0 |
| Term.getPowrIdx() | 1.0 | 1.0 | 1.0 |
| Term.getSinIdx() | 1.0 | 1.0 | 1.0 |
| Term.hashCode() | 1.0 | 1.0 | 1.0 |
| Term.isZero() | 1.0 | 1.0 | 1.0 |
| Term.negate() | 1.0 | 1.0 | 1.0 |
| Term.setIdx(Function,BigInteger) | 1.0 | 1.0 | 1.0 |
| Term.Term() | 1.0 | 1.0 | 2.0 |
| Term.Term(BigInteger,BigInteger...) | 1.0 | 1.0 | 1.0 |
| Term.toString() | 5.0 | 11.0 | 15.0 |
| Tri.derive() | 1.0 | 1.0 | 1.0 |
| Tri.isZero() | 1.0 | 1.0 | 1.0 |
| Tri.Tri(Function,BigInteger) | 1.0 | 1.0 | 1.0 |
| Total | 112.0 | 151.0 | 174.0 |
| Average | 1.2584269662921348 | 1.696629213483146 | 1.9550561797752808 |
可以看到,除了inputparser外(上述情况见1.2.1),Term类的toString类的ev过高,与第一次作业类似,是使用了过多if 语句对多种不同情况进行了特判,造成复杂的逻辑分支。可以对对特殊情况进行汇总。
(3) 第三次作业
第三次作业复杂得多。在第二次作业的架构基础上,分离Term与Factor分离,并且沿用了**抽象类BasicFunction**的设计, 用于继承常数、幂函数(x)、三角嵌套函数4种基本函数类。同时,所有函数类都实现了Derivative接口,用于应用表达式和求 导时表达式类的工厂模式。
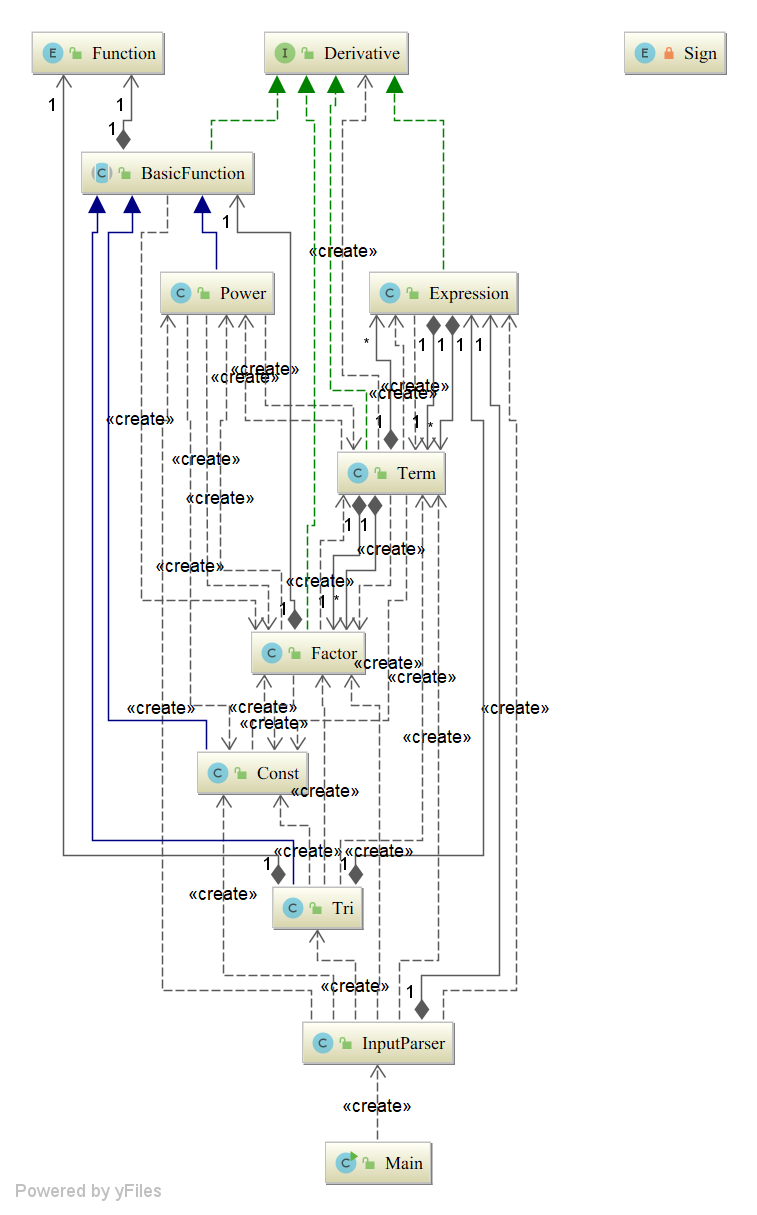
| Term.toString() | 8.0 | 10.0 | 13.0 |
| Term.put(Derivative) | 4.0 | 6.0 | 6.0 |
| Term.mult(Derivative) | 6.0 | 8.0 | 9.0 |
| Term.isFactor() | 4.0 | 5.0 | 8.0 |
| Expression.simplify() | 5.0 | 6.0 | 6.0 |
| Term.divide(Derivative) | 5.0 | 6.0 | 7.0 |
上图仅仅列出了度量分析中较高的部分方法,其中对于mult(),divide()方法都要分别针对三种情况进行处理,没有单独建立 方法,修改建议是可以利用多态原则单独实现三个方法。toString三项指标都过高,ev过高也是为了特判输出情况所有有了对 if的重复利用。这一点的修改我还没有想好,但对整体代码影响不大。
针对类的度量分析,总结以下针对代码架构冗杂的可能的解决方法:
**1.运用多态原则,尽可能地减少if-else分支。** **2.对于与本类相关性不高的方法,如Expression里的simplify方法,可以单独拎出来新建一个类,或者使用static的静态 方法。**
3.对于冗杂的循环,灵活使用stream,addall,iterator等已经造好的轮子。
4.不妨用AbsractCollection的抽象集合类代替冗杂的嵌套有多个list的类,如List
### 1.3 优化策略
#### 1.3.1 多项式
第一节多项式优化较为简单。仅仅需要
1)合并同类项。
2)如果存在非负项,将非负项提前至第一位。
即可达到多项式最短。
1.3.2 三角函数多项式
在第一节优化的基础上,第二节多增加了对于恒等式$sin2x+cos2x=1$的化简,共分为六种子情况。利用DFS遍历,在规定时
间内寻找可能的最短输出。
1.3.3 带嵌套的函数多项式
在第一节优化的基础上,增加了使用递归提取公因式的优化,在规定时间内寻找可能的最短输出。
2.错误分析
2.1 错误分析
(1) 第一次作业
公测和互测均无错误。
(2)第二次作业
公测和互测均无错误。
错误点提示:化简时进行DFS需要设置时间限,以防出现TLE。
(3)第三次作业
第三次作业在公测和互测中都出现了TLE的错误,比如cos(sin(cos(cos((-cos(sin(sin(cos(cos(sin(x^2)))))))))))
。经检查,发现是由于Term类的clone()方法(含有多个set和list类的克隆)的层层嵌套导致了时间复杂度呈指数型增长。把诸
多内部的list合并,即将Term修改为继承抽象集合collection类,重新实现clone()方法以及对应的迭代器,减少递归嵌套的时
间复杂度。
3.自动化测试
3.1 基于Python的压力测试
仿照1.2.1的语法规则,为了偷懒,自测和互测中都使用自动数据生成器。根据正则表达式,利用Python提供的xeger包生成随机 字符串,比如其中的随机生成表达式函数如下(dataMaker.py):
```python def randompoly(): poly = "" if randint(0, 1): poly += newXeger.xeger(sign) poly += randomterm() times = randint(0,10) for i in range(0, times): poly += newXeger.xeger(sign) + randomterm() return poly ```
同时,利用sympy库的diff接口,同时很容易地实现了结果正确性的比较(compare.py):
```python def compare(origin,answer): x = Symbol("x") diffFunc = diff(eval(origin),x) ans = eval(answer) for i in range(testcase): test = (rd.random()*20 - 10) if trans(diffFunc.subs("x",test)) - trans(ans.subs("x",test)) >= small: return False; return True; ```
3.2 互测对拍器
互测的测试全程交给对拍器。对拍程序的设计思路很简单,即
- 生成测试数据。
- 将测试数据分别输入到标称与自己的代码,并获得输出。
- 对比两个输出是否相同。
第一步我们交给3.1的数据生成器dataMaker.py,最后一步交给3.1的数据比较器compare.py。中间只需要实现java
工程在windows下的正常编译即可:
sb.Popen('javac'+'-cp'+'classes\\'+classname+'-sourcepath'+'classes\\'+classname +path+'-encoding utf8')
### 3.3 利用JUnit组件
JUnit可以自动运行,检查自己的结果,并提供即时反馈,节省了手动梳理错误的时间。另外,易于定位bug,解决单元
测试的问题,比如哪一个函数出错,哪一个函数没有输出之类的问题等等。在这里,我们仅仅用来进行批量测试:
@Test
public void test1() throws Exception {
new EnhancedUserTestTools(Main.class, 2000)
.testAll(new File("./test/input_test.txt"), new File("./test/output_test.txt"));
}
当然,其他用法也很多,可以自行查找,在这里不做赘述。
### 3.4 注意
随机生成也要有一定的局限性,我们无法保证完全覆盖。此次互测中因为随机生成器的嵌套层数设置,导致没有测试到TLE的
不过。类似的极端的测试样例很有可能存在,比如形似$(sin^2x + 1)\times (sin^2x + 1) \times (sin^2x + 1)$的
表达式,当然,这种情况在此次作业中为不合法输入。
4.工厂设计模式
什么是工厂设计模式?
> **意图:** 定义一个创建对象的接口,让其子类自己决定实例化哪一个工厂类,工厂模式使其创建过程延迟到子类进行。 > > **主要解决:** 主要解决接口选择的问题。 > > **何时使用:** 我们明确地计划不同条件下创建不同实例时。 > > **如何解决:** 让其子类实现工厂接口,返回的也是一个抽象的产品。 > > **关键代码:** 创建过程在其子类执行。 > > **优点:** > > 1. 扩展性高,如果想增加一个产品,只要扩展一个工厂类就可以。 > 2. 屏蔽产品的具体实现,调用者只关心产品的接口。 > > **缺点:** 每次增加一个产品时,都需要增加一个具体类和对象实现工厂,使得系统中类的个数成倍增加,在一定程度 上增加了系统的复杂度,同时也增加了系统具体类的依赖。这并不是什么好事。 > > **注意事项:** 作为一种创建类模式,在任何需要生成复杂对象的地方,都可以使用工厂方法模式。有一点需要注意的 地方就是复杂对象适合使用工厂模式,而简单对象,特别是只需要通过 new 就可以完成创建的对象,无需使用工厂模式。 如果使用工厂模式,就需要引入一个工厂类,会增加系统的复杂度。
可以看出,在此次作业中,InputParser类和BasicFunction类就是我们的工厂:InputParser类先解析字符串,构建 Expression,Term,Factor三种表达式类型,但并不需要知道表达式内部存储的信息;而BasicFunction类也是一个关于 Factor的工厂,他不关心下面究竟是常数,幂函数或是三角函数,只需要关心basicfunction需要实现的基本接口(求导, 乘法等等)。
