Matplotlib案例入门

Matplotlib模块依赖于NumPy模块和tKinter模块，可以通过该模块绘制多种形式的图形，包括线图、直方图、饼状图、散点图和误差线图等。是计算结果可视化的重要工具

绘制带有中文标签和图例的正弦余弦曲线

关于line2D的详细可以参考这篇博客

import numpy as np
import pylab as pl
import matplotlib.font_manager as fm

myfont = fm.FontProperties(fname=r'C:\Windows\Fonts\STKAITI.ttf') # 设置字体
t = np.arange(0.0,2.0*np.pi,0.01) # 自定义取值范围
s = np.sin(t)
c =np.cos(t)
pl.plot(t,s,label='正弦')
pl.plot(t,c,label='余弦')
pl.xlabel('x-变量',fontproperties ='STKAITI',fontsize=24) # 设置x轴标签
pl.ylabel('y-正弦余弦函数值',fontproperties='STKAITI',fontsize=24)# 设置y轴标签
pl.title('sin-cos函数图像',fontproperties='STKAITI',fontsize=32) # 图形标题
pl.legend(prop=myfont) # 设置图例
pl.show()

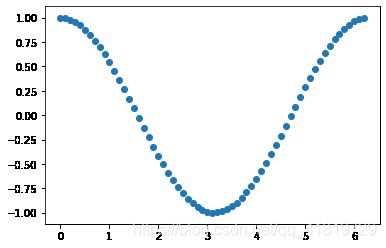
绘制散点图

a = np.arange(0,2.0*np.pi,0.1) # 取值范围
b = np.cos(a)
pl.scatter(a,b) # 分别传入x,y，用scatter创建散点图
pl.show()

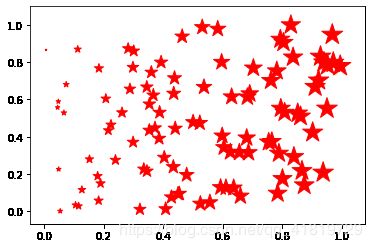
使用随机数生成数值，并根据数值大小来计算散点的大小。

import matplotlib.pylab as pl
import numpy as np

x  = np.random.random(100) # 生成一个一维ndarray对象x,其中包含100个0~1的随机数,这些随机数作为x轴坐标
 
y = np.random.random(100) # 生成100个随机数作为y轴坐标

pl.scatter(x,y,s=x*500,c=u'r',marker=u'*') # s 指定大小（x越大，星星越大），c指定颜色,marker指定符号形状
pl.show()

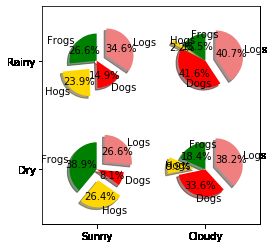
绘制饼状图

def pie(x, explode=None, labels=None, colors=None, autopct=None,
        pctdistance=0.6, shadow=False, labeldistance=1.1, startangle=None,
        radius=None, counterclock=True, wedgeprops=None, textprops=None,
        center=(0, 0), frame=False, rotatelabels=False, hold=None, data=None)

参数详解：

参数	说明
x	(每一块)的比例，如果sum(x) > 1会使用sum(x)归一化；
labels	(每一块)饼图外侧显示的说明文字；
explode	(每一块)离开中心距离；
startangle	起始绘制角度,默认图是从x轴正方向逆时针画起,如设定=90则从y轴正方向画起；
shadow	在饼图下面画一个阴影。默认值：False，即不画阴影；
labeldistance	label标记的绘制位置,相对于半径的比例，默认值为1.1, 如<1则绘制在饼图内侧；
autopct	控制饼图内百分比设置,可以使用format字符串或者format function '%1.1f’指小数点前后位数(没有用空格补齐)；
pctdistance	类似于labeldistance,指定autopct的位置刻度,默认值为0.6；
radius	控制饼图半径，默认值为1；
counterclock	指定指针方向；布尔值，可选参数，默认为：True，即逆时针。将值改为False即可改为顺时针。
wedgeprops	字典类型，可选参数，默认值：None。参数字典传递给wedge对象用来画一个饼图。例如：wedgeprops={‘linewidth’:3}设置wedge线宽为3。
textprops	设置标签（labels）和比例文字的格式；字典类型，可选参数，默认值为：None。传递给text对象的字典参数。
center	浮点类型的列表，可选参数，默认值：(0,0)。图标中心位置。
frame	布尔类型，可选参数，默认值：False。如果是true，绘制带有表的轴框架。
rotatelabels	布尔类型，可选参数，默认为：False。如果为True，旋转每个label到指定的角度。

import numpy as np
import matplotlib.pyplot as plt

# The slices will be ordered and plotted counter-clockwise切片将按逆时针方向排列和绘制
labels = "Frogs", "Hogs", "Dogs", "Logs"
sizes = [15, 30, 45, 10]
colors = ['green', 'gold', '#FF0000', 'lightcoral']
explode = (0, 0.1, 0, 0.1)  # only 'explode' the second and fourth slice只分离第二片和第四片饼
fig = plt.figure()
ax = fig.gca() # 下面的所有pie都将绘制在一个figure容器中
ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True,
       startangle=90,
       radius=0.25, center=(0, 0), frame=True)

ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90,
       radius=0.25, center=(1, 1), frame=True)

ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90,
       radius=0.25, center=(0, 1), frame=True)

ax.pie(np.random.random(4), explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90,
       radius=0.25, center=(1, 0), frame=True)

# 设置figure容器的边框性质
ax.set_xticks([0, 1]) # 设置边框x的角标
ax.set_yticks([0, 1]) 

ax.set_xticklabels(["Sunny", "Cloudy"]) # 设置边框x角标对应的标签
ax.set_yticklabels(["Dry", "Rainy"])

ax.set_xlim((-0.5, 1.5))
ax.set_ylim((-0.5, 1.5))

# Set aspect ratio to be equal so that pie is drawn as a circle
ax.set_aspect('equal')

plt.show()

绘制多个图像

多个图像一起显示

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,2*np.pi,500)
y = np.sin(x)
z = np.cos(x*x)

plt.figure(figsize=(8,4)) # 设置整张图的长宽

# 标签前后加上$可以使用内嵌的LaTex引擎将其显示为公式
plt.plot(x,y,label ='$sin(x)$',color='red',linewidth=2) # 红色，两个像素宽
plt.plot(x,z,'b--',label='$cos(x^2)$') # 蓝色，虚线

plt.xlabel('Time(s)')
plt.ylabel('Volt')
plt.title('Sin and Cos figure using pyplot')
plt.ylim(-1.2,1.2)  # 设置y轴的范围
plt.legend() # 显示图示
plt.show() # 显示绘图窗口

多个图像单独显示，即子窗口

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 2 * np.pi, 500)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x * x)

# 创建一个总视图figure
plt.figure(1)
# 创建3个子视图
# 2x2的格子中，第一个格子存放一个子视图
ax1 = plt.subplot(2, 2, 1)
# 第二个格子存放子视图
ax2 = plt.subplot(2, 2, 2)
# 第三和第4个格子合并为第三个子视图
ax3 = plt.subplot(2, 1, 2)

lim = (-1.2,1.2) # y轴统一在这个限制内

# 通过plt.sca(choose)选择子视图
plt.sca(ax1)
# 在第一个子视图内画图
plt.plot(x, y1, color='red')
plt.ylim(lim) # 设置y轴范围
# 选择第二个子视图
plt.sca(ax2)
plt.plot(x,y2,'b--')
plt.ylim(lim)
# 选择第三个子视图
plt.sca(ax3)
plt.plot(x,y3,'g--')
plt.ylim(lim)
plt.legend()
plt.show()

No handles with labels found to put in legend.

绘制三维曲面

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d # 画3D图形需要额外导入这个包

x,y=np.mgrid[-2:2:20j,-2:2:20j] # 必须使用mgrid创建三维图形的栅栏(x,y轴)
z = 50*np.sin(x+y)
ax = plt.subplot(111,projection='3d')
ax.plot_surface(x,y,z,rstride=2,cstride=1,cmap=plt.cm.Blues_r)

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

import numpy as np
import pylab as pl
import mpl_toolkits.mplot3d


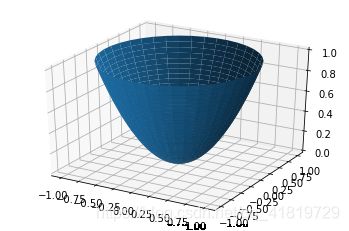
rho,theta=np.mgrid[0:1:40j,0:2*np.pi:40j] # rho 半径，theta 角度
z= rho**2 # z=r^2
x = rho*np.cos(theta) # x=rcos(a)
y = rho*np.sin(theta) # y=rsin(a)
ax = pl.subplot(111,projection='3d')
ax.plot_surface(x,y,z) # 绘制曲面图
pl.show()

绘制三维曲线

from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt


fig = plt.figure()
ax = fig.gca(projection='3d')
theta = np.linspace(-4*np.pi,4*np.pi,100)
z = np.linspace(-4,4,100)*0.3
r=z**3+1
x = r*np.sin(theta) # x=rsin(a)
y = r*np.cos(theta) # y=rcos(a)
ax.plot(x,y,z,label='parametric curve')
ax.legend()
plt.show()