多项式求导,每周一次重构,十分充实。
作业分析
第一次作业
作业要求
第一次作业比较简单,只有常数项和幂函数。
思路
在看了指导书之后,本来打算的是按照指导书提到的一个思路,也就是正则表达式的方法来做。
后来与学姐交流后,决定尝试递归下降分析法。这种方法可以完全按照指导书给出的表达式的定义来分析所给表达式,判断wf和提取项、因子,都很方便。即分析表达式->分析项->分析因子,结束后返回,在这个过程中就可以获得两个ArrayList,再进行求导、排序、合并就不多说了。
关于优化。首先就是合并同类项,这很好实现。最后看讨论区学到了进一步的优化方法,即把系数为正的项放在前面,这样可以省去一个可能的加号。感谢大佬的分享的思路,第一次作业强测满分。
基于度量的分析
uml图
只有一个类,仍然是面向过程的思想,就不放图了。
复杂度分析
一个三百多行的类,复杂度果断红。
部分方法的复杂度过高,其中全红的Item中全是if、else。除去整体的分析,还在很多地方加了对遍历是否结束的判断,代码有些混乱。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| MainClass.Item() | 11 | 17 | 19 |
| MainClass.Var() | 1 | 9 | 9 |
| MainClass.hb_output(ArrayList |
1 | 9 | 9 |
| MainClass.output(TreeMap |
1 | 27 | 28 |
| MainClass.start() | 1 | 4 | 5 |
关于bug
第一次作业较为简单,大多数同学都没有什么错误。
第二次作业
作业要求
在第一次作业的基础上加上了sin(x)和cos(x)。
加上了wf的判断。
思路
首先进行wf的判断。由于这次保证了没有空白字符引起的wf,那就仍然可以去掉所有的空白字符再进行处理。
利用正则表达式
String regExp = "(sin)|(cos)|(\\()|(\\))|(\\d+)|(\\+)|(\\-)|(\\*\\*)|(\\*)|(x)|(\\s)|(\\S)";
提取出所有的token,判断是否是合法字符,返回true或者false。
如果字符都是合法的,那就可以进行字符串的处理并进一步判断wf。
每一个项都可以表示为一个四元组,所以这次我建立了一个类Item。仍然利用递归分析,获取所有的项。然后利用这些项,构建了类Poly。在Poly中,对每一项进行求导。
关于优化,对于每一项,根据幂指数、sin(x)的指数、cos(x)的指数排序,这里建立了Key类用于排序,以便于对所有可以利用sin(x)^2+cos(x)^2=1的项进行化简;最后根据系数排序,同样是找到系数为正的项放在第一位。
基于度量的分析
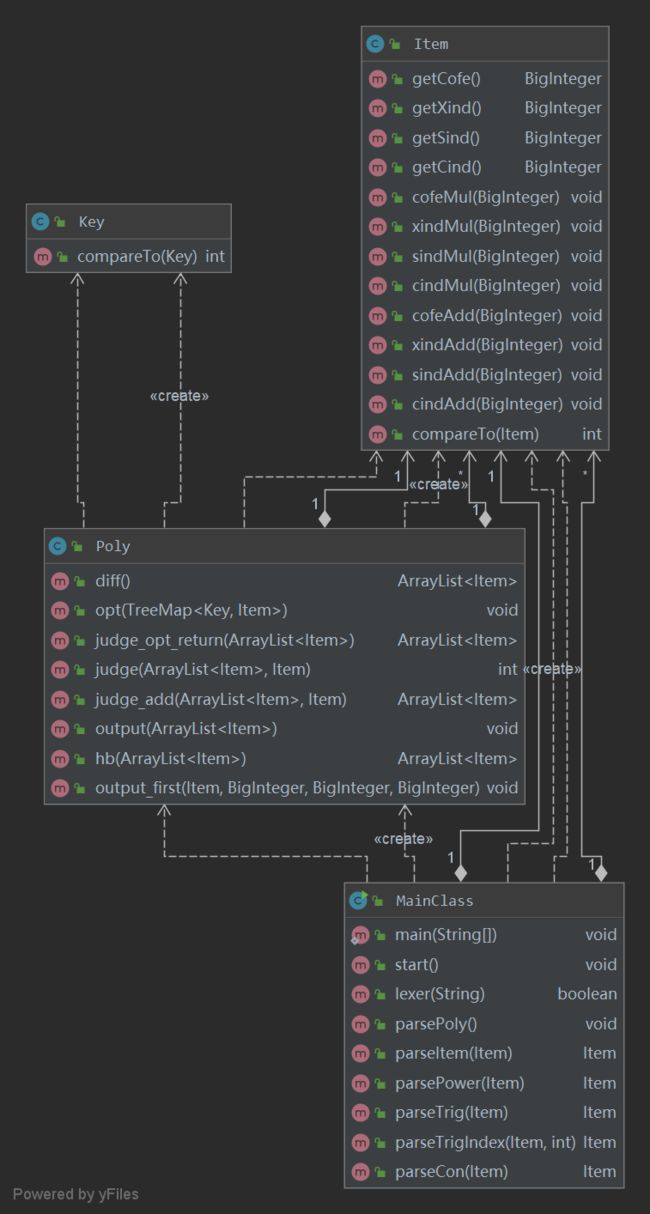
uml图
Class Metrics
MainClass里面有一个递归分析的过程,Poly里面有求导和优化的全过程,果然复杂度很高。
Method Metrics
这是飘红的一些方法,占了总方法数的约一半。然而都是主要的方法,其他的都是很简单的一些运算之类。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Key.compareTo(Key) | 7 | 6 | 7 |
| MainClass.lexer(String) | 5 | 6 | 7 |
| MainClass.parseItem(Item) | 9 | 18 | 20 |
| MainClass.parsePoly() | 5 | 12 | 13 |
| MainClass.parsePower(Item) | 4 | 12 | 12 |
| MainClass.parseTrig(Item) | 6 | 12 | 13 |
| MainClass.parseTrigIndex(Item,int) | 4 | 8 | 9 |
| Poly.diff() | 1 | 9 | 9 |
| Poly.judge_add(ArrayList |
1 | 13 | 13 |
| Poly.opt(TreeMap |
4 | 6 | 6 |
| Poly.output_first(Item,BigInteger,BigInteger,BigInteger) | 1 | 16 | 16 |
关于bug
自己用自动评测跑了很久,然后互测的时候被hack一刀,一脸懵逼。最后才发现,我在判断新加入的一项是否可以与前面的某一项合并的时候,如果合并了,flag = 1,但是在判断能否合并的时候忘记假如flag不等于零的条件,而且这里也没有合并同类项的操作,就导致对于某些数据,它可以合并两次,然后就bug了。
然后放着评测跑了一晚上,果然就找到了......所以是随机生成数据并测试的时间还是不够久。
第三次作业
作业要求
加入嵌套,也就是因子中加入了表达式因子。
思路
首先写的还是递归分析判断wf,有了前两次的经验,写起来就很顺手了。虽然第三次要求更加复杂,但是与前两次的相比,这次的思路反而更加清晰,由于第一次主要用来提取数据,第二次则是在提取数据时还进行了部分wf的判断,导致这两次的递归都有些混乱。在第三次作业将wf判断完全与数据处理和求导分开,相比之下清楚了许多。
在求导之前去掉了所有空白项,合并了所有可以合并的加减符号便于后面处理。
Poly中有Item项的ArrayList,Item中有Ele的ArrayList,建立接口,对传入的因子进行判断并生成对应类型的因子。然后递归求导,获得最后结果。
关于优化,只判断并去除了零项,放弃了同类项的合并还有常数的计算,由于第二次作业留下的心理阴影,这次选择多测一测代码而不是优化。最后发现强测中需要优化的部分并不是很多,性能分也不少。
基于度量的分析
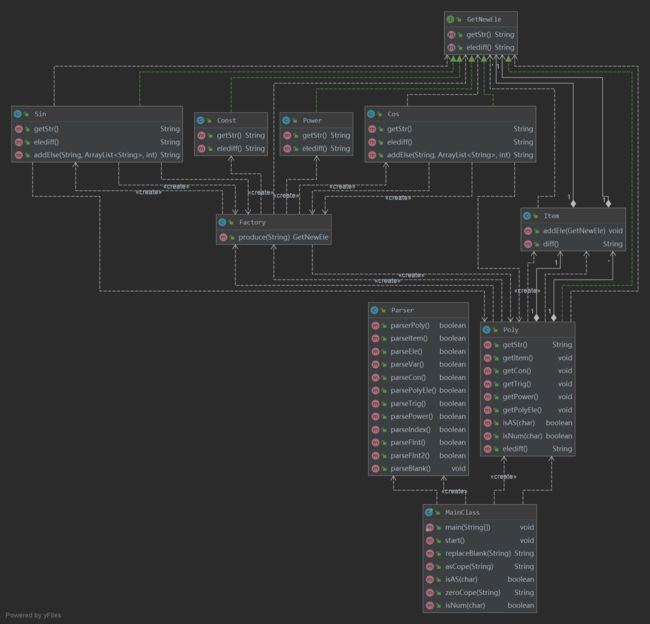
uml图
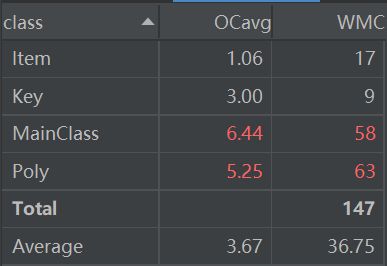
Class Metrics
除了求导很简单的常数因子和幂函数因子的类以外,其他的没一个复杂度是低的。
| Class | OCavg | WMC |
|---|---|---|
| Const | 1 | 3 |
| Cos | 4.5 | 18 |
| Factory | 11 | 11 |
| Item | 5 | 15 |
| MainClass | 3.57 | 25 |
| Parser | 6.15 | 80 |
| Poly | 4.8 | 48 |
| Power | 2 | 6 |
| Sin | 4.25 | 17 |
Method Metrics
也是列出了复杂度超标的。同样是主要的一些方法全部复杂度过高。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Cos.elediff() | 3 | 9 | 10 |
| Factory.produce(String) | 11 | 11 | 16 |
| Item.diff() | 6 | 9 | 13 |
| MainClass.zeroCope(String) | 1 | 9 | 11 |
| Parser.parseEle() | 10 | 10 | 15 |
| Parser.parseFInt() | 5 | 5 | 9 |
| Parser.parseFInt2() | 5 | 7 | 10 |
| Parser.parseIndex() | 5 | 4 | 6 |
| Parser.parseItem() | 10 | 8 | 15 |
| Parser.parsePolyEle() | 6 | 5 | 8 |
| Parser.parsePower() | 5 | 4 | 7 |
| Parser.parseTrig() | 12 | 11 | 19 |
| Parser.parseVar() | 5 | 4 | 6 |
| Poly.getItem() | 6 | 11 | 15 |
| Poly.getTrig() | 4 | 6 | 10 |
| Sin.elediff() | 4 | 8 | 9 |
关于复杂度的一个小总结,跟大佬的代码对比了之后才发现自己代码复杂度有多高。之前写作业的时候并没有使用这个插件进行分析,对复杂度也没有足够的重视。
要写出优秀的代码只有通过测试当然是不行的,代码风格(每次checkstyle都会炸裂)、还有复杂度,以后都需要更多关注。
关于bug
强测全过但是互测被砍了15刀就很惨......原来是递归求导时间太久。
后来修复时发现,自己在一些部分中,明明可以只进行一次的求导操作进行了两次,这就导致在递归的时候,每次求导都会多进行一次,这样时间就成了指数级的增加。我将求导的结果暂存然后使用,就解决了该问题。
发现别人的bug
手写评测,整体思路就是在python中随机生成表达式然后利用sympy计算表达式并比较结果。其中生成表达式部分,按照指导书中给出的形式化表述,递归生成数据。在第三次作业中,由于刚开始设置的递归层数太多导致生成数据出现错误,还对递归生成表达式因子的层数进行了限制(然后自己就因为忘记测试超多层嵌套被hack了)。
在发现别人的错误后还会手动对数据进行化简并多次测试,尝试推测错误所在,尽量不交同质数据。
存在的问题
尤其是在第三次作业中,sympy的计算结果会有误差,偶尔出现虚假错误信息。这个时候就需要利用其他的方法或者手动进行进一步比较。
应用对象创建模式来重构
对wf的判断仍然可以用递归来完成,这样可以完全保证判断是足够完善的。但是问题就是这样做方法复杂度会比较高,判断wf的类也会比较复杂。
分类可以更加详细。将输入的字符串转换为一系列token之后,对每一个token进行实例的转换,包括各种操作符,左/右括号,数字,三角函数,空白符等等。
然后建立工厂,根据参数传入的表达式,创建它所代表的表达式,建立表达式树。
之后利用表达式树进行求导和化简。
心得体会
第一次作业完全没有面向对象的意识,相比之下,第二次、第三次算是在转变。
关于第三次作业,对比了自己与一份优秀作业,深切感受到了差距。
自己的思维一直都是,“这样做可以解决问题,而且写起来比较简单,那就这么做吧“。没有考虑可迭代性,导致重构了两次,每次作业与前一次关系都不太大。虽然最后的分数都还凑合,但是相比之下设计就显然要差很多。
此外,java的功能十分强大,而自己了解的实在还不够,所以有一些用法是无论如何都不会想到。
下次在完成作业时,会多注意重构的问题,尽量让后面的作业都可以以前面的作业为基础来完成。