OO第一单元总结

1 基于度量来分析自己的程序结构

第一次作业：

uml类图：

 

 

其中main函数在Expression类中，Amalgamate类解析输入的格式，Expression类中为计算和合并。

Polynomial类为多项式类，该类将输入数据实例化为一个个多项式对象，该类的变量有系数，常数以及两个判定是否为系数和是否被Expression类中compute方法计算的boolean类型变量。

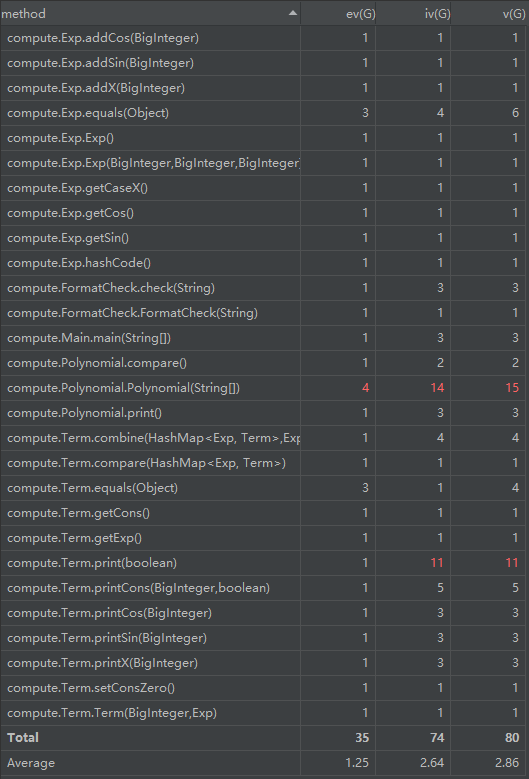
度量分析：

 

 由此可以看出Expression.out的圈复杂度和模块设计复杂度较高，软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。所以此部分还可以做出优化。

第二次作业：

UML类图：

 

 

FormatCheck类为字符串格式检查，Exp类记录的是多项式类型，并提供了一系列接口，Term类实现的则是整个多项式的合并方法，Polynomial类为多项式类，该类实现了对多项式的求导。

度量分析：

 

 由此可以看出Polynomial.Polynomial方法的圈复杂度和模块设计度比较高，也是因为这部分是多项式求导的计算部分，所以复杂度较高。

第三次作业：

UML类图：

 

 

 

 

 

 

第三次作业比较复杂，三个包加一个main函数类，compute包主要是多项式求导计算，包括DiffExpression类，PrintTree类和Simplify类；expression包主要是多项式对象建立和多项式树的建立，包括Builder类、Checker类、Operate类和Tree类；factor包是每一个多项式的因子，包括父类Factor，以及四个子类。expression包中：Tree类为树的初始化类，包括左右节点以及计算符号op和因子factorOperate类定义了每一种op的全局定义，方便后面计算。Checker类为对输入的数据进行格式检查和建立树。compute包中：DiffExpression类主要进行多项式求导的方法，建立两个树，一个是输入树，一个是输出树，并通过PrintTree类中printPoly方法输出数据。

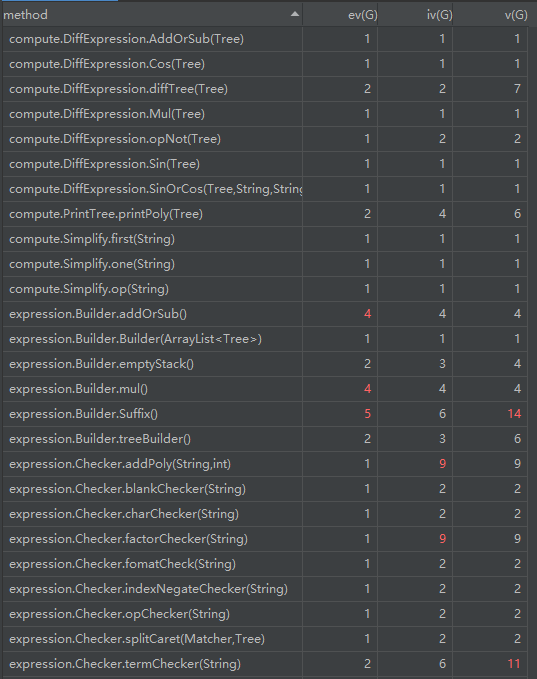
度量分析：

 

 

 

 由此可见树的建立方法和求导计算方法比较复杂，此部分也存在一些问题，后面会提。

2 分析自己的程序bug：

第一次作业：无

第二次作业：第二次作业存在的主要bug是正则表达式部分存在一些问题，应该在先进行illegal检查后，再删去空格，再检查括号内是否为x，这样可以防止（x ）、（ x）、（ x ）类似类型报错。格式检查先删去空格，然后再每一项结束增加空格，再通过split拆分为一个一个多项式

第三次作业：第三次作业存在设计问题，在DiffExpression类的求导计算中，无法处理类似sin（cos（x））这样的嵌套三角函数问题。

3 分析自己发现别人程序bug所采用的策略：

先通过阅读别人的代码，特别是正则表达式部分，在理解了逻辑之后再进行测试。

4 应用对象创建模式

三次作业中除了求导在同一个类中计算，每一个类的每一种方法都不是特别复杂，x sin cos分别在不同的类创建，在计算方面还可以进行优化。

5 对比心得体会

优秀的代码层次分明，在此还需要改进，以后的作业应该尽量早点开始，早点优化。提高代码的复用性，减少代码的重构，不重复造轮子。