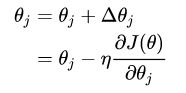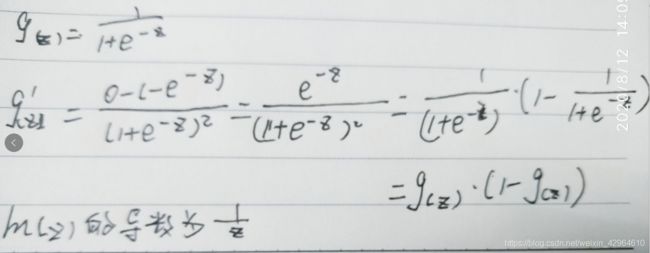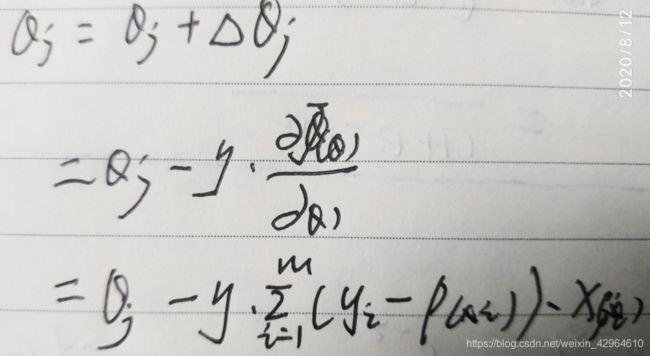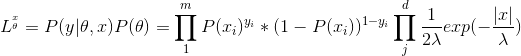机器学习算法之逻辑回归总结
简介
逻辑回归虽然名字中有回归两字,但其属于分类算法的一种,常用于二分类问题,但其也可以适用于多分类,本文主要针对二分类进行说明,逻辑回归因其形式简单,模型的可解释性非常好,资源占用小,尤其是内存等优势在工业中界应用比较广泛,逻辑回归用一句话可以概括为:逻辑回归假设数据服从伯努利分布,通过极大似然函数的方法,运用梯度下降来求解参数,来达到二分类的目的,可以看到其包含了挺多知识点:假设、极大似然函数(损失函数)、梯度下降(求解方法)、二分类(目的)等,在介绍逻辑回归算法原理之前先来复习几个数学知识点。
相关数学知识
以简单的语句讲解逻辑
伯努利分布
一个事件只有发生和不发生两种情况,这样的分布称为伯努利分布,如:日常生活中的男、女比例,抛硬币等。
知识扩展:二项分布:N重伯努利分布
极大似然估计
参考链接:极大似然估计
在了解极大似然估计之前我们先讲讲两个名词:概率、统计,大家觉得这两个词一样么?
简单说下:概率研究的问题为根据已知模型和参数,去预测产生的结果,而统计则是根据数据,去预测模型和参数,即:概率是已知模型和参数,推数据,统计是已知数据,推模型和参数。
接来下我们来讲讲贝叶斯公式,这个大家应该都清楚(需要了解条件概率、先验概率和后验概率,不了解的请自行百度),其公式为:
![]()
其求解的问题为在事件B发生的情况下A发生的概率。在极大似然估计中我们使用到了似然函数,似然这个词和概率其实差不多,但却是两个不同的概念,对于函数P(x|y),其输入有两个:x表示某一个具体的数据;y表示模型的参数。
- 如果y已知,x变量则为概率函数,它描述对于不同的样本点 x ,其出现概率是多少。
- 如果x已知,y变量则为似然函数,它描述对于不同的模型参数,出现 x这个样本点的概率是多少。
极大似然估计,通俗来讲:就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
简单来说就是换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即模型已定,参数未知。
别人博客中的例子:
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?
很多人马上就有答案了:70%。而其后的理论支撑是什么呢?
我们假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜 色服从同一独立分布。
这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中,七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。
如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样,我们可以得到如下表达式:
P(样本结果|Model)
= P(x1,x2,…,x100|Model)
= P(x1|Mel)P(x2|M)…P(x100|M)
= p^70(1-p)^30.
好的,我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数,也就是求的式中的p。
那么我们怎么来求这个p呢?
不同的p,直接导致P(样本结果|Model)的不同。
好的,我们的p实际上是有无数多种分布的。如下:
那么求出 p^70(1-p)^30为 7.8 * 10^(-31)
p的分布也可以是如下:
那么也可以求出p^70(1-p)^30为2.95* 10^(-27)
那么问题来了,既然有无数种分布可以选择,极大似然估计应该按照什么原则去选取这个分布呢?
答:采取的方法是让这个样本结果出现的可能性最大,也就是使得p^70(1-p)^30值最大,那么我们就可以看成是p的方程,求导即可!
那么既然事情已经发生了,为什么不让这个出现的结果的可能性最大呢?这也就是最大似然估计的核心。
我们想办法让观察样本出现的概率最大,转换为数学问题就是使得:
p^70(1-p)^30最大,这太简单了,未知数只有一个p,我们令其导数为0,即可求出p为70%,与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。
概率分布
这里通过几个例子给大家说明几个名词
概率函数:对于离散型随机变量可以通过一个例子说明,如:掷骰子1-6,概率函数为某个取值的概率,即:1/6
概率分布:对于离散型随机变量,如:掷骰子1-6,每个个取值的概率的一个分布表
概率分布函数:对于离散型随机变量,其为累积概率函数。
概率密度函数:对于连续型随机变量,其为概率分布函数的导数
L1/L2范数
范数,是具有“距离”概念的函数,在数学上,范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。使用机器学习方法解决实际问题时,我们通常要用L1或L2范数做正则化(regularization),从而限制权值大小,减少过拟合风险。特别是在使用梯度下降来做目标函数优化时
L1范数
概念:非零向量的绝对值之和,比如 向量A=[1,-1,3], 那么A的L1范数为 |1|+|-1|+|3|。
L1范数,使得学习得到的结果满足稀疏化,从而方便提取特征。L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和
L1正则化服从拉普拉斯分布,其公式为
L2范数
概念:向量的平方和再开方,比如 向量A=[1,-1,3], 那么A的L1范数为![]() 。
。
L2范数是我们最常见最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数,L2范数通常会被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
L2正则化服从高斯分布,其公式为:
算法原理
基本原理
首先来说两个基本的假设:
1、假设结果服从伯努利分布,即:最终分类结果为两个类型,其中:P(Y=1|x)=p(x)、P(Y=0|x)=1-p(x)
2、假设样本为正的概率符合逻辑回归算法的拟合函数(sigmond函数):![]()
损失函数,损失函数是机器学习中的重要概念,其中逻辑回归选择的损失函数为极大似然函数,如下:
似然函数是相乘的模型,我们可以通过取对数将等式右侧变为相加模型,然后将指数提前,以便于求解。对其取对数,同时我们的目的是将所得似然函数极大化,而损失函数是最小化,因此,我们需要在上式前加一个负号便可得到最终的损失函数,即:
求解其最大值可以通过梯度下降的方式进行求解,其迭代公式为:
其中即可通过求解损失函数的偏导数进行求解,推导过程如下:
在求导过程中有两个数学知识点,对sigmoid函数求导和对数求导,如下:
最后将求得的梯度带入迭代公式中,即为:
其实,常用梯度下降有三个种方法,可以根据需要选择,分别是:批量梯度下降(BGD),随机梯度下降(SGD),small batch梯度下降。
逻辑回归的损失函数为什么要使用极大似然函数作为损失函数?
损失函数一般有四种:平方损失函数、对数损失函数、HingeLoss0-1损失函数、绝对值损失函数,逻辑回归使用的是极大似然函数,其对对数以后等同于对数损失函数,根据梯度下降的迭代公式,可以看出,其更新只和x、y的更新速度相关,和sigmod函数本身的梯度是无关的。这样更新的速度是可以自始至终都比较的稳定。为什么不选平方损失函数的呢?其一是因为如果你使用平方损失函数,你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。
正则化
参考文档:逻辑回归的相关知识
正则化是一个通用的算法和思想,所有会产生过拟合现象的算法都可以使用正则化来避免过拟合。
一般我们采用L1和L2范式
L1正则化
LASSO回归,相当于为模型添加了这样一个先验知识:w 服从零均值拉普拉斯分布。 由于引入先验知识,所以似然函数为:
对其取对数,即可得到其损失函数,等价于原始损失函数的后面加上了 L1 正则,因此 L1 正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识。
L2正则化
Ridge 回归,相当于为模型添加了这样一个先验知识:w 服从零均值正态分布。同样的引入先验知识,可以自己讲之前的高斯分布公式带入得到
L2正则化等价于原始的损失函数后面加上了 L2 正则,因此 L2 正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验知识。
Sklearn包的介绍
首先逻辑回归算法包的导入,如下:
from sklearn.linear_model import LogisticRegression接下来我们对其所涉及到的参数进行说明,如下:
class sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)其中:
- penalty正则化选择,可选择‘l1’, ‘l2’, ‘elasticnet’, ‘none’,默认'l2'
- dual:是否选择对偶,当n_samples> n_features时,首选dual = False
- tol:算法停止的误差条件,默认是0.0001
- C:正则强度的倒数;必须为正浮点数,较小的值指定更强的正则化,默认为1.0
- fit_intercept:是否应将常量(也称为偏差或截距)添加到决策函数。默认是True。
- intercept_scaling:不常用
- class_weight:对类别进行加权,可以使用字典形式加权,输入‘balanced’代表权重为类别频率,默认是"None"。
- random_state:选择随机种子,打乱样本时候指定,确保实验选取的随机值相同,有利于模型对比
- solver:指定优化器类型,可选‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’
- max_iter:算法收敛的最大迭代次数,默认100。
- multi_class:不常用。
- verbose:对于liblinear和lbfgs,求解器将verbose设置为任何正数以表示详细程度。
- warm_start:不常用。
- n_jobs:使用内核数。
- l1_ratio:弹性网络参数,其中0 <= l1_ratio <=1。仅当penalty=“ elasticnet”时使用。
其返回的标签如下:
- classes_:返回的类别标签
- coef_:系数
- intercept_:截距项
- n_iter_:所有类的迭代次数
实战案例
本文使用sklearn中的数据集,具体代码如下:
首先导入所需的相关数据包,如下:
from sklearn import datasets
import numpy as np
# 划分数据
from sklearn.model_selection import train_test_split
# 标准化
from sklearn.preprocessing import StandardScaler
# 导入逻辑回归算法
from sklearn.linear_model import LogisticRegression导入数据并划分数据集,如下:
iris = datasets.load_iris()
# 选取特征项(选取了所有特征)
x = iris["data"][:,:]
# 选取目标值
y = iris["target"]
## 30%测试数据,70%训练数据,stratify=y表示训练数据和测试数据具有相同的类别比例
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=1,stratify=y)对数据进行标准化处理,如下:
# 数据预处理(标准化)
sc = StandardScaler()
sc.fit(x_train)
x_train_std = sc.transform(x_train)
x_test_std = sc.transform(x_test)模型训练,如下:
# 模型选择
lr = LogisticRegression(C=100.0,random_state=1,solver="lbfgs")
# 模型训练
lr.fit(x_train_std,y_train)
# 预测
lr.predict(x_test_std)
# 表示每个样本的预测概率
lr.predict_proba(x_test_std)




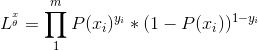
![J_{\theta }=-ln(L^{_{\theta }^{x}})=-\sum _{1}^{m}\left [ y_{i}lnP(x_{i})+(1-y_{i})ln(1-P(x_{i})) \right ]](http://img.e-com-net.com/image/info8/49ad4eb593e242d6890c13544f6ee9da.gif)