第一单元总结
一、第一次作业
1.题目概况:
第一次作业是整个单元作业的基础,即简单多项式求导。其中对带符号整数、幂函数和项、表达式等概念均有详细的形式化表达。第一次作业保证输入合法。在保证得出正确答案的前提下,性能上要求答案输出越短越好。
2.思路:
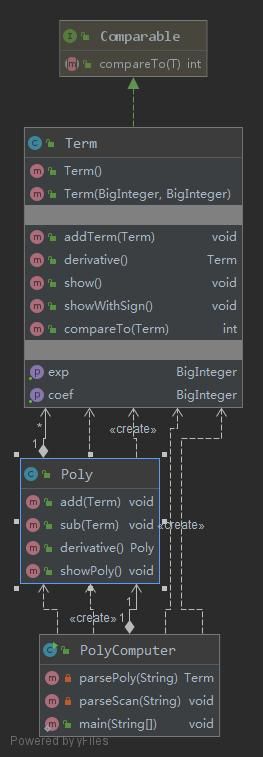
总体来说第一次作业的实现可以分为三部分:表达式的解析、求导和结果的输出,在这次作业中我主要采用了三个类:PolyComputer(主类)、Term(项类)、Poly(表达式类)。具体实现如下:
- 表达式的解析:
- 预处理:由于第一次作业保证输入合法,因此可以大胆的将输入简化以方便后续处理,使用
scan = scan.replaceAll("[ \\t]", "")去除标准输入中无用的空白字符即可。 - 解析项:这一步主要是输入一个字符串,来返回其相应的Term类。Term类有两个属性:coef(指数)、exp(系数)。解析项的实现依托于正则表达式。首先根据是否能匹配到字符x来判断是否为常数,如果是常数则构造的项系数为0;不为常数则继续判断是否有不为1的指数,据此构造出一个项。
- 解析表达式:这里则是传入标准输入,然后返回一个完整的Poly(表达式)。Poly类中采用
ArrayList来存储每一项。也是采用正则表达式来不断向后匹配项,每匹配到一项就将字符串传入上一步提到的parseTerm函数中解析项,并将返回的项添加到Poly的ArrayList里。
- 预处理:由于第一次作业保证输入合法,因此可以大胆的将输入简化以方便后续处理,使用
- 求导:
在Term类中构造了求导函数,因为第一次作业只要求简单多项式求导,因此用到的公式较为简单。这里是返回了一个新的Term对象。Poly的求导则是遍历ArrayList中的每一个Term,将导数添加到一个新的Poly中,构成了导数。 - 结果的输出:
在第一次作业中我一时没想到用toString来输出表达式,而是专门写了一个show函数,来在函数中直接输出相应的项、多项式。(后来回想起来才发现这种输出方式极其不灵活,且面对更复杂的表达式时十分不利,也埋藏下了潜在的bug,在第二次作业中就改用了toString) - 性能优化:
- 为了使输出的表达式更短,第一次作业所能做的就是合并同类项,这一点在构造表达式的过程中就可以实现,即每次添加项时,都会遍历ArrayList,若发现系数相同,直接改变原有项的指数,不用再添加进ArrayList;若没发现相同的,就直接添加进去。
- 在show函数中,也添加了一些判断语句,比如系数为1时不输出系数、指数为+-1时只输出+-号等等。同时,为了使整个表达式更短,将存储项的容器按照系数由大到小sort一下,这样如果有正系数项的话一定会放在最前面,相比负系数项在最前面,最终的结果可以省略一个+。
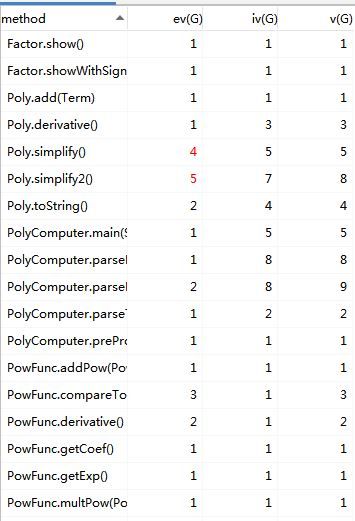
3.度量分析:
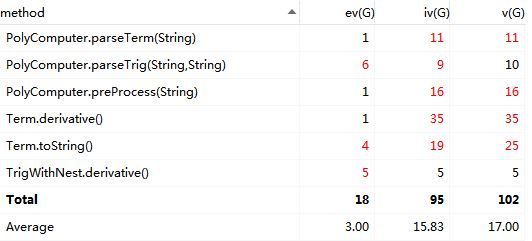
由于第一次作业整体结构较为简单,所以大部分方法复杂度都较低,程序结构也比较清晰。但仍有三个方法复杂度较高:即表达式添加、删减项和项的输出。基本复杂度过高说明非结构化程度高,难以模块化和维护,项的输出方法设计复杂度较高,因为其中调用的方法也较多,耦合度高,这些都不利于代码的维护和拓展,说明自己还是受面向过程的思想影响。进一步优化应该从降低模块耦合度入手,让每个方法功能更明确,尽量避免一个方法里调用多个其他方法。
第二次作业
1.题目概况:
第二次作业在第一次作业的基础上增加了三角函数和幂函数一起作为因子,每一项也变成了一个或多个因子相乘。除此之外,加入了输入合法性判断,但依然保证不会出现因空格导致的输入WF。同样性能上输出结果越短越好。
2.思路:
这次作业由于上一次作业的类太少,且可拓展性不高,所以基本上重构了一遍,不过第一次作业留下来的代码也有能用在第二次里面的,如上一次的Term类可以改造成PowFunc(幂函数)类。相比上次,这次作业使用了继承关系,增加了一个Factor(因子)的父类,两个子类PowFunc和TrigFunc(三角函数)继承自Factor类,修改了Term类,仍使其用ArrayList来容纳Factor。
- WF判断:
WF判断还是靠的正则表达式,由于上一次作业已经根据概念的形式化表达写出了正则,这次只需增加一些项,然后对输入匹配整个表达式正则,如果不成功则直接输出WF;匹配成功就替换掉空白字符然后开始解析表达式。 - 表达式的解析、求导:
这次解析表达式与上次类似,增加了解析三角函数的过程。求导也是类似,增加了乘法求导法则的应用。虽然项的因子数不确定,但每一项可简化为a*x**b*sin(x)**c*cos(x)**d这种形式。 - 结果的输出:
这次的结果输出吸取了上次教训,采用了toString来实现,发现这样确实灵活了不少,在自己调试的时候也能据此随时观察对象的状态,化简时可以对比长度,整体结果输出时也能对返回的字符串进行处理。 - 性能优化:
- 输入过程的优化:在往项里添加因子时直接合并好幂函数、三角函数。
- 结果的优化:对于结果得到的表达式类,进行二层优化:1.合并同类项。检测是否有幂函数、三角函数的指数都相同的项,检测到后直接系数相加合并;2.递归化简。运用
sin(x)**2 + cos(x)**2 = 1来化简,遍历每一项,如果有sin项就提取出sin(x)**2变成1 - cos(x)**2,其他项直接加入,然后看分裂sin得到的表达式长度是否小于原表达式,如果小于就对分裂sin得到的表达式继续这一过程,直到长度不再变化。
3.度量分析:
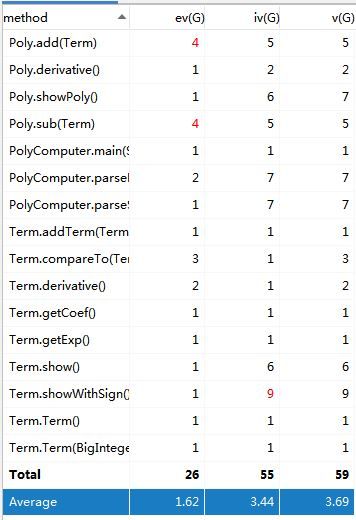
可以看出随着作业更加复杂,设计的耦合度和复杂度也升高了不少。特别是求导、toString、化简等核心方法复杂度都比较高。再看看自己写的代码,发现有些方法确实有些臃肿,需要进一步改进,比如一些方法里if-else层层叠加,其实这些都可以更细分化。
第三次作业
(题外话:本次作业过程中出了一点点小意外。在本人于周五将第一版通过中测的代码提交上去后,满心欢喜地去睡觉然后想着第二天怎么测试找bug然后再优化输出。第二天(周六)也确实花了一天找到了不少bug,顺便做了一些优化。但是,在晚上9:35才把最终版提交上去,结果因为复制粘贴出了差错,导致有一个点没过!!!在花了几分钟纠结是不是要再修改回来提交最终版后,为了稳健我还是选择了提交第一版,结果可想而知,自己早已预料到强测公测会在哪爆炸QAQ...所以得出了一个教训:一定要给自己留够时间来应对特殊情况,绝对不要等到最后一刻才交上去)
1.题目概况:
这次作业的整体难度和复杂度都有了较大提升。变化主要有两点:1.三角函数允许嵌套因子;2.增加了表达式因子。WF,输出的长短都要考虑。
2.思路:
作业的主要难度集中在三角函数的解析和输入合法性判断上,因为三角函数允许嵌套,所以增加了一个继承自TrigFunc(三角函数)的TrigWithNest(带嵌套的三角函数)类,解析也采用了递归解析。
- 预处理以及合法性判断:
由于嵌套带来的多层括号问题很难解决,直接用正则匹配括号无论是贪婪还是非贪婪都可能出错。在看了讨论区dalao的帖子后,我采用了将最外层小括号( )换成[ ]的做法(又复习了一遍数据结构),这样直接匹配sin[]、cos[]、[表达式],对于方括号里面的东西递归解析即可。在确定不是WF后才把空白字符替换掉。 - 解析三角函数:
在TrigWithNest类中定义Poly属性nest,在解析三角函数中先不管方括号内是什么,直接将嵌套内容提取出来,检测是否WF,如果不是就处理一下(去掉多余括号)传入解析表达式的方法中,返回的一个Poly作为三角函数的nest。求导时用链式法则即可解决。 - 性能优化:
(虽然没交上去,但还是讲一下...)因为在最初构造时只考虑了结果正确性,性能优化什么都没考虑,就造成了各种*(1)、((((((x))))))这种冗长的输出。首先解决三角函数内层括号数问题,在Poly类和Term类分别增加了numOfTerm(项个数)、numOfFactor(因子个数)的属性。如果三角函数嵌套的表达式只有一项,且这一项里只有一个因子,那么就不用输出两层括号了(一点例外就是如果把x**2简化成x*x了,那么就不能只有一层括号了,虽然它在项里仍只算一个因子)。针对表达式因子的输出,在toString之后如果最外层是几对括号,去除掉直到只剩一层。合并同类项等等同上,还有其他的点比如遇到(1)表达式作为因子就不用加到str里、有一个*(0)直接返回"0"等等。
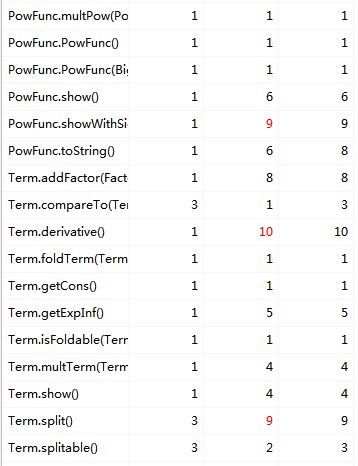
3.度量分析:
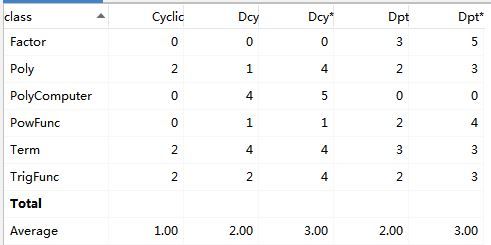
可以看出这次的设计一些模块的复杂度还是很高,特别是三角函数求导部分和解析部分。回想自己的设计确实有一个方法过于复杂,判断和调用过于频繁的情况。在设计时应该尽量遵循高内聚低耦合的设计原则,让每个模块功能更明确。而且这次作业在继承上也有不妥之处(比如Factor类其实设计成接口或者抽象类比较合适、之前的TrigFunc类在后来没有用处或许可以删掉,一些操作如化简、判断合法性可以单独封装成一类等等)。总之,这次作业在可拓展性、复杂度方面都有很大的提高空间。
四、BUG分析
第一、二次作业在强测中未被发现bug,但互测中却很不幸被hack了,第一次bug的造成原因是为了提高性能,对于表达式的0项不进行输出,如果只有一个0就输出0,但忽略了表达式有多个0项的情况,导致0*x**2+0这种结果就没有输出(这也是没用toString的坏处);第二次则是输出-1时只输出了符号-,说到底这两个bug都是自己的疏忽大意造成的,实在不应该。
第三次因为自己的失误,导致bug较多。1.解析三角函数时由于是根据匹配到sin还是cos来决定生成哪种类型,因为判断语句的先后关系就导致cos(sin(x))这种情况也会匹配到sin,于是就生成了sin(sin(x))这样的,导致结果出错。解决方法是改成匹配sin[来确定三角函数类型,就不会被嵌套函数所影响;2.对于- + -1这种有三个符号的项判断合法性会错判成WF,解决方法是增加特判,遇到这种情况不会判定为WF。
总的来说,这些bug分布在程序的一些细微之处,但对整体影响又很大,正如课堂上所讲的“二八定律”,往往bug出现在代码核心片段。以后测试代码时应该更加仔细一些,细枝末节的地方不可忽视。
五、互测策略
在第一次互测中本人采用的是很笨的方法,即把每个人的代码下下来放到IDEA里面先大致浏览一遍,然后一个个的测试,这种方法不仅效率低,还很令人烦躁,光是一个样例就要花近1分钟的时间来给每个人测试。第二次互测因忍受不了低效的手动测试,尝试自己写测评机。在阅读讨论区dalao的帖子后,我采用了一种简单的方式,即用python对代码进行批量自动化测试,步骤如下:
- 手动给每份代码打成jar包(eclipse的export功能),并放到一个文件夹里
- 利用python的Xeger库根据正则表达式自动生成上百份测试样例放入
in.txt中,同时用sympy库来生成对应的结果,存入res.txt - run()函数:利用
os.system('java -jar jar/' + name + '.jar< in.txt' + ' >> ' + name + '.txt')语句运行jar文件,这一步会得到以每个人名字命名的结果文件 - check()函数:利用sympy函数,读取正确结果和测试结果,两者相减再代值判断求导是否正确,将结果(AC或WA)输出到一个文件里
利用这个自动测评机,成功地发现了别人的两个bug(在求导结果上出错误)。
第三次测评时,由于样例的复杂性,用正则就不便于自动生成了,只能自行写测试样例。关于测试样例的构造,我是采取的从简单到逐渐复杂的方法,例如先构造整数项、幂函数项、简单三角函数项,然后逐渐加入表达式因子、三角函数嵌套函数、正负号变复杂、边界数据等等,尽量覆盖测试面。对于有进行优化的代码,我会针对优化部分设计特殊的样例来检测是否出现优化错误。还有一点就是,在自己设计过程中发现bug的样例记录下来,在互测中也能用到。写好一堆样例后,之前的自动测试还是能用在检测正确性方面的,最后hack别人近二十次。总体来说,自动测评机确实好用,互测效果还可以。
六、应用对象创建模式
由于第三周实验时才接触到创建模式,还不是很了解,所以作业中没有大规模运用到创建模式,只是用到了一些继承关系。在实验中,我也切身感受到了工厂模式的优越性:在一个父类有多个子类时,创建过程教给Factory很方便,模块功能明确,且可拓展性强,并且能降低代码耦合度。
对于这一单元代码的重构改进,我认为可以用到创建模式。例如题目中提到的因子,都有共同类型的方法比如求导、合并,也有相似的属性如指数等等,可以采用因子抽象类,让幂函数、三角函数或者表达式继承这个抽象类,再实现各自的方法。至于因子的构造,全部交给一个Factory类来实现。而一些特定功能的方法,也可以将它们封装成一个类,比如专门化简的类、专门解析多项式的类、判断合法性的类等等,这样写出来的代码条理清晰,可拓展性强,且容易维护。
七、对比与心得体会
在拜读了几份优秀代码后,发现自己的设计仍有很大的提高空间。优秀的代码结构总是非常合理的,对于每个功能都有专门的类进行实现,具有高内聚低耦合的特点。而且有的采用了工厂模式,便于后续的拓展。自己的代码则耦合程度略高,有的方法过于复杂冗长,表达不够简洁,而且对容器的使用较为单一,导致一些方法过于麻烦,其实有其他各有特点的容器更方便使用。总而言之还需要多学习。
传闻中的OO果然足够硬核。这几周写的代码量和代码复杂程度是之前从未有过的,“圣杯战争”也很是刺激。在一次次的作业练习中,我已经体会到了java这类面向对象编程语言的好处,也从一些犯过的错误中吸取了不少教训。这只是OO课程的一个开始,后面的挑战也会更多,自己一定要摆脱怠惰的心理,在作业上多思考,多肝几天,将学到的创建模式多运用运用,加深对面向对象思想的认识。
最后,感谢为这门课付出了许多的老师和助教们!