UnityShader_玻璃效果,以及关于视口坐标、透视投影的投影矩阵推导过程
玻璃效果实现原理:
先抓取一张玻璃后面景象的贴图tex;将tex根据玻璃法线纹理做一个扭曲得到 color1;
计算玻璃本身的反射颜色(使用上篇说得天空盒子)color2;
将color1和color2按照一定比例混合;
Shader "Unity Shaders Book/Chapter 10/Glass Refraction" {
Properties {
_MainTex ("Main Tex", 2D) = "white" {}
_BumpMap ("Normal Map", 2D) = "bump" {}
_Cubemap ("Environment Cubemap", Cube) = "_Skybox" {}
_Distortion ("Distortion", Range(0, 10000)) = 10 //扭曲程度
_RefractAmount ("Refract Amount", Range(0.0, 1.0)) = 1.0 //混合系数,反射和屏幕截取图混合系数
}
SubShader {
Tags { "Queue"="Transparent" "RenderType"="Opaque" }
GrabPass { "_RefractionTex" } //利用屏幕后处理技术抓取的物体后面抓取图
Pass {
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
sampler2D _MainTex;
float4 _MainTex_ST;
sampler2D _BumpMap;
float4 _BumpMap_ST;
samplerCUBE _Cubemap;
float _Distortion;
fixed _RefractAmount;
sampler2D _RefractionTex;
float4 _RefractionTex_TexelSize;//纹素 纹素=1/像素 256*256图片的纹素大小为(1/256,1/256),就是单位像素的大小,作为屏幕大小的度量单位
struct a2v {
float4 vertex : POSITION;
float3 normal : NORMAL;
float4 tangent : TANGENT;
float2 texcoord: TEXCOORD0;
};
struct v2f {
float4 pos : SV_POSITION;
float4 scrPos : TEXCOORD0;
float4 uv : TEXCOORD1;
float4 TtoW0 : TEXCOORD2;
float4 TtoW1 : TEXCOORD3;
float4 TtoW2 : TEXCOORD4;
};
v2f vert (a2v v) {
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
//计算屏幕坐标
o.scrPos = ComputeGrabScreenPos(o.pos);
o.uv.xy = TRANSFORM_TEX(v.texcoord, _MainTex);
o.uv.zw = TRANSFORM_TEX(v.texcoord, _BumpMap);
float3 worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;
fixed3 worldNormal = UnityObjectToWorldNormal(v.normal);
fixed3 worldTangent = UnityObjectToWorldDir(v.tangent.xyz);
fixed3 worldBinormal = cross(worldNormal, worldTangent) * v.tangent.w;
o.TtoW0 = float4(worldTangent.x, worldBinormal.x, worldNormal.x, worldPos.x);
o.TtoW1 = float4(worldTangent.y, worldBinormal.y, worldNormal.y, worldPos.y);
o.TtoW2 = float4(worldTangent.z, worldBinormal.z, worldNormal.z, worldPos.z);
return o;
}
fixed4 frag (v2f i) : SV_Target {
float3 worldPos = float3(i.TtoW0.w, i.TtoW1.w, i.TtoW2.w);
fixed3 worldViewDir = normalize(UnityWorldSpaceViewDir(worldPos));
// 从法线纹理图提取出法线方向
fixed3 bump = UnpackNormal(tex2D(_BumpMap, i.uv.zw));
// 计算法线空间中的扭曲偏移量
// 详解:法线的x,y 方向 * 扭曲 * 纹素(单位) = 纹素单位下的偏移
float2 offset = bump.xy * _Distortion * _RefractionTex_TexelSize.xy;
//对原屏幕获取坐标的z方向做一个偏移,其实不使用i.scrPos.z 也可以的,这里的作用暂时不清楚,希望有好心人解惑!
i.scrPos.xy = i.scrPos.xy + offset * i.scrPos.z;
//计算折射颜色,关于i.scrPos.xy/i.scrPos.w 其实是屏幕坐标,其原理在后面会详说
fixed3 refrCol = tex2D(_RefractionTex, i.scrPos.xy/i.scrPos.w).rgb;
//将切线空间法线转为世界空间下
bump = normalize(half3(dot(i.TtoW0.xyz, bump), dot(i.TtoW1.xyz, bump), dot(i.TtoW2.xyz, bump)));
fixed3 reflDir = reflect(-worldViewDir, bump);
fixed4 texColor = tex2D(_MainTex, i.uv.xy);
//计算反射颜色
fixed3 reflCol = texCUBE(_Cubemap, reflDir).rgb * texColor.rgb;
//反射折射的混合比例
fixed3 finalColor = reflCol * (1 - _RefractAmount) + refrCol * _RefractAmount;
return fixed4(finalColor, 1);
}
ENDCG
}
}
FallBack "Diffuse"
}
关于GrabPass的使用说明如下图,摘自《UnityShader入门精要》 冯乐乐!

填坑(下面的推导都是建立在透视投影的基础上)
1、视口坐标推导
文章中唯一比较难懂的地方是下面代码的 i.scrPos.xy/i.scrPos.w ,其实在之前的镜像水面的时候已经用过了,但是当时没有去深入研究,几天来填这个坑。
o.pos = UnityObjectToClipPos(v.vertex);
o.scrPos = ComputeGrabScreenPos(o.pos);
.
.
.
.
fixed3 refrCol = tex2D(_RefractionTex, i.scrPos.xy/i.scrPos.w).rgb;
首先,我们要知道这个东西计算的是 模型的 “视口坐标”! ,在Unity当中,视口空间的左下角是(0,0),右上角是(1,1),就是像素宽,像素高。
下面开始推导:
1、整个过程梳理:
①模型空间->剪裁空间: UnityObjectToClipPos(v.vertex);
②剪裁空间->视口空间 (使用齐次除法转化成2D坐标)
PS. ComputeGrabScreenPos(o.pos);这步其实只是为计算屏幕2D坐标做了准备
其中①又可以分成(Unity已经帮我们封装好了方法,但是要知根知底):
(1)模型空间->世界空间
(2)世界空间->观察空间/相机空间
(3)观察空间->剪裁空间 (使用投影矩阵进行转换)
2、我们令o.pos = (clipx,clipy,clipz,clipw)
PS后面会有剪裁空间相关的推导
3、把顶点从 剪裁空间 投影到 视口空间 生成对应的2D坐标,我们常用的方法是 齐次除法(透视除法) ,就是用齐次坐标系的 x、y、z 分量去除以 w 分量。 在OpenGL中,我们把这一步叫做 归一化的设备坐标(NDC)。
因此我们可以得到屏幕空间的 (x,y,z) = (clipx/clipw, clipy/clipw, clipz/clipw)
剪裁空间 经过 齐次除法(透视除法) 后会变换到一个立方体内。在OpenGL中,这个立方体的x、y、z∈[-1,1],而在DirectX中x、y、z∈[0,1],Unity采用了OpenGL的齐次剪裁空间,如下图。

4、接下来只要把 x、y∈[-1,1]转化到 [0,1]的区间内(视口空间的下的坐标是∈[0,1]) ,我们使用线性插值计算一下视口空间坐标
x − ( − 1 ) 1 − ( − 1 ) = s c r e e n x − 0 1 − 0 \frac{ x-(-1)}{1-(-1)} \quad = \quad {screen~x~-0\over 1-0} 1−(−1)x−(−1)=1−0screen x −0
即 v i e w p o r t x = x + 1 2 即viewport~x~= \frac{ x+1}{2} 即viewport x =2x+1
又 因 为 x = c l i p x c l i p w , 所 以 我 们 可 以 得 到 又因为 x= \frac{clip~x~}{clip~w~},所以我们可以得到 又因为x=clip w clip x ,所以我们可以得到
v i e w p o r t x = c l i p x c l i p w + 1 2 = c l i p x 2 ∗ c l i p w + 1 2 viewport~x~= \frac{ \frac{clip~x~}{clip~w~}+1}{2} = \frac{clip~x~}{2*clip~w~} \quad +\frac{1}{2} viewport x =2clip w clip x +1=2∗clip w clip x +21
同 理 可 以 求 出 s c r e e n y = c l i p y 2 ∗ c l i p w + 1 2 同理可以求出screen~y~= \frac{clip~y~}{2*clip~w~} \quad +\frac{1}{2} 同理可以求出screen y =2∗clip w clip y +21
5、我们再来看看 i.scrPos 是什么东西

上图是从Unity的 “UnityCG.cginc” 库中找到的关于计算屏幕坐标的定义,其中宏定义UNITY_UV_STARTS_AT_TOP是判断图形api平台是否为non-OpenGL,我们是使用的OpenGL,所以scale = 1
我们得到 o = (clipx/2 + clipw/2 , clipy/2 + clipw/2 , clipz , clipw )
所以 i.scrPos.xy/i.scrPos.w 就是
x = c l i p x 2 c l i p w + 1 2 x =\frac{ clip~x~}{2clip~w~} \quad + \quad {1\over 2} x=2clip w clip x +21
y = c l i p y 2 c l i p w + 1 2 y =\frac{ clip~y~}{2clip~w~} \quad + \quad {1\over 2} y=2clip w clip y +21
是不是与我们上面计算的视口坐标一致!
2、透视投影的投影矩阵的推导
如下图, 透视投影 是将一个视椎体变换到一个正方体上

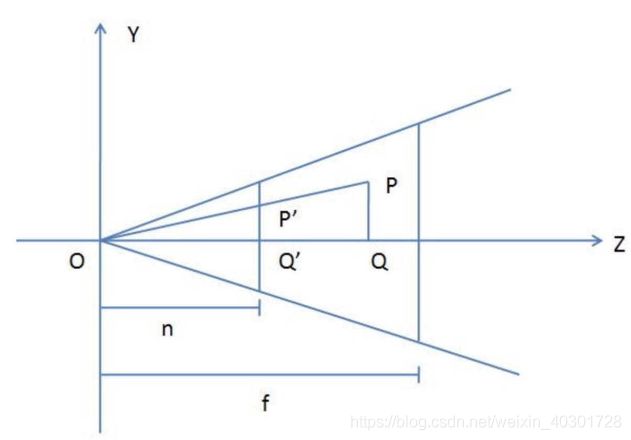
如上图所示,投影矩阵是将 视椎体 内的点 投射到 近平面 上,以上图的 P 点为例,投影点 P’ 点是 P与原点O在近平面上的交点,设P=(x,y,z),P’=(x’,y’,z’)
利用差值算法
0 − x ′ 0 − x = n 0 − z 得 到 \frac{ 0-x'}{0-x} \quad=\quad {n\over 0-z}得到 0−x0−x′=0−zn得到
x ′ = − n x z 同 理 可 得 y ′ = − n y z x'= -n\frac{x}{z}同理可得y'= -n\frac{y}{z} x′=−nzx同理可得y′=−nzy
下面我们用反推的方法来计算
( n 0 0 0 0 n 0 0 a 1 a 2 a 3 a 4 b 1 b 2 b 3 b 4 ) ∗ ( x y z 1 ) = ( n x n y ? 1 ? 2 ) = > ( 齐 次 除 法 ) = ( − n x z − n y z ? z 1 ) \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ a_1 & a_2 & a_3 & a_4 \\ b_1 & b_2 & b_3 & b_4 \\ \end{pmatrix}* \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ ?_1 \\ ?_2 \\ \end{pmatrix} =>(齐次除法)= \begin{pmatrix} -n\frac{x}{z} \\ -n\frac{y}{z} \\ ?_z \\ 1 \\ \end{pmatrix} ⎝⎜⎜⎛n0a1b10na2b200a3b300a4b4⎠⎟⎟⎞∗⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nxny?1?2⎠⎟⎟⎞=>(齐次除法)=⎝⎜⎜⎛−nzx−nzy?z1⎠⎟⎟⎞
由上面最后一次经齐次除法可知,?2 = -z ,所以可以推出 b1=b2=b4=0 ,b3=-1,所以上式转为
( n 0 0 0 0 n 0 0 a 1 a 2 a 3 a 4 0 0 − 1 0 ) ∗ ( x y z 1 ) = ( n x n y ? 1 − z ) = > ( 齐 次 除 法 ) = ( − n x z − n y z ? z 1 ) \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ a_1 & a_2 & a_3 & a_4 \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}* \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ ?_1 \\ -z \\ \end{pmatrix} =>(齐次除法)= \begin{pmatrix} -n\frac{x}{z} \\ -n\frac{y}{z} \\ ?_z \\ 1 \\ \end{pmatrix} ⎝⎜⎜⎛n0a100na2000a3−100a40⎠⎟⎟⎞∗⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nxny?1−z⎠⎟⎟⎞=>(齐次除法)=⎝⎜⎜⎛−nzx−nzy?z1⎠⎟⎟⎞
我们知道P(x,y,z)是三角片元上的三条边上的某一个点,因此xyz两两之间存在着线性关系,我们可以得到
{ x = A z + B y = C z + D \begin{cases} x=Az+B \\ y=Cz+D \end{cases} {x=Az+By=Cz+D
又 ∵ { x = − x ′ n z y = − y ′ n z 又∵\begin{cases} x=-\frac{x'}{n}z \\ y=-\frac{y'}{n}z \end{cases} 又∵{x=−nx′zy=−ny′z
∴ { − x ′ n z = A z + B − y ′ n z = C z + D = > { 1 z = E x ′ + F 1 z = G y ′ + H 即 1 z 与 x ′ 、 y ′ 是 线 性 关 系 的 ∴\begin{cases} -\frac{x'}{n}z=Az+B \\ -\frac{y'}{n}z=Cz+D \end{cases} => \begin{cases} \frac{1}{z}=Ex'+F \\ \frac{1}{z}=Gy'+H \end{cases}即\frac{1}{z}与x'、y'是线性关系的 ∴{−nx′z=Az+B−ny′z=Cz+D=>{z1=Ex′+Fz1=Gy′+H即z1与x′、y′是线性关系的
所以我们可以令 a1 =a2=0 a3=a a4=b
( n 0 0 0 0 n 0 0 0 0 a b 0 0 − 1 0 ) ∗ ( x y z 1 ) = ( n x n y a z − b − z ) = > ( 齐 次 除 法 ) = ( − n x z − n y z − a z − b z 1 ) \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}* \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ az-b \\ -z \\ \end{pmatrix} =>(齐次除法)= \begin{pmatrix} -n\frac{x}{z} \\ -n\frac{y}{z} \\ -\frac{az-b}{z} \\ 1 \\ \end{pmatrix} ⎝⎜⎜⎛n0000n0000a−100b0⎠⎟⎟⎞∗⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nxnyaz−b−z⎠⎟⎟⎞=>(齐次除法)=⎝⎜⎜⎛−nzx−nzy−zaz−b1⎠⎟⎟⎞
接 下 来 只 要 把 z 限 制 在 [ − 1 , 1 ] 即 { − a z − b z = − 1 , 当z=-n ∵0-z=n y = C z + D , 当z=-f ∵ 0-z=f = > { a = − f + n f − n b = − 2 f n f − n 接下来只要把z限制在[-1,1]即 \begin{cases} -\frac{az-b}{z}=-1, & \text{当z=-n ∵0-z=n} \\ y=Cz+D , & \text{当z=-f ∵ 0-z=f} \end{cases} => \begin{cases} a=-\frac{f+n}{f-n} \\ b=-\frac{2fn}{f-n} \end{cases} 接下来只要把z限制在[−1,1]即{−zaz−b=−1,y=Cz+D,当z=-n ∵0-z=n当z=-f ∵ 0-z=f=>{a=−f−nf+nb=−f−n2fn
接下来我们还要把x、y限制在[-1,1],我们设限制后的点为(x’’,y’’)
x ′ − l r − l = x ′ ′ − 1 1 − ( − 1 ) 得 到 x ′ ′ = 2 x ′ − l r − l + 1 再 把 上 面 的 x ′ 带 入 得 到 \frac{ x'-l}{r-l} \quad = \quad {x''-1\over 1-(-1)}得到x''=2\frac{ x'-l}{r-l} \quad+1再把上面的x'带入得到 r−lx′−l=1−(−1)x′′−1得到x′′=2r−lx′−l+1再把上面的x′带入得到
x ′ ′ = 2 n r − l ( − x z ) − r + l r − l 同 理 得 到 y ′ ′ = 2 n t − b ( − y z ) − t + b t − b x''=\frac{ 2n}{r-l}(-\frac{x}{z}) \quad-\frac{r+l}{r-l}同理得到 y''=\frac{ 2n}{t-b}(-\frac{y}{z}) \quad-\frac{t+b}{t-b} x′′=r−l2n(−zx)−r−lr+l同理得到y′′=t−b2n(−zy)−t−bt+b
因此我们得到完整的投影矩阵为
( 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ) \begin{pmatrix} \frac{ 2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{ 2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} ⎝⎜⎜⎛r−l2n0000t−b2n00r−lr+lt−bt+b−f−nf+n−100−f−n2fn0⎠⎟⎟⎞
针对《UnityShader入门精要》中的情形做变形
只要把对应的
n=Near
f=Far
r=nearClipPlaneWidth/2
l=-nearClipPlaneWidth/2
t=nearClipPlaneHeight/2
b-nearClipPlaneHeight/2
∠FOV对应的转化带入及可到Mfrustum
计算涉及到的相关图片已经在下面列出
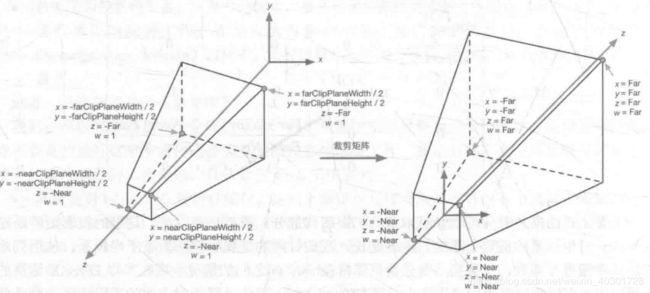




xy参考
z参考
走流程了喂! 诚心欢迎讨论,欢迎私信!