深度学习2-4
第二章:线性代数
2.1 标量、向量、矩阵和张量
- 标量:一个标量就是一个数。
- 向量:
第三章:概率论与信息论
3.2 随机变量
随机变量是可以随机地取不同值的变量。一个随机变量只是对可能的状态的描述,它必须伴随一个概率分布来指定每个状态的可能性。
3.3 概率分布
概率分布用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。
3.3.1 离散型变量和概率质量函数
离散型变量的概率分布可以用概率质量函数来描述。概率质量函数将随机变量能够取得的每个状态映射到随机变量取得该状态的概率。
x ∼ P ( x ) x\sim P(x) x∼P(x):随机变量 x x x遵循分布 P ( x ) P(x) P(x)。
⋆ \star ⋆联合概率分布:概率质量函数可以同时作用于多个随机变量,这种多个变量的概率分布被称为联合概率分布。 P ( X = x , Y = y ) P(X=x,Y=y) P(X=x,Y=y)表示 X = x X=x X=x和 Y = y Y=y Y=y同时发生的概率。简记为 P ( x , y ) P(x,y) P(x,y)。
⋆ \star ⋆ 概率质量函数的定义:
如果一个函数 P P P是随机变量 x x x的概率质量函数 P M F PMF PMF,必须满足下面3个条件:
(1): P P P的定义域必须是 x x x的所有可能状态的集合。
(2): ∀ x ∈ X , 0 ≤ P ( x ) ≤ 1. \forall x\in X,0\leq P(x)\leq 1. ∀x∈X,0≤P(x)≤1.
(3): ∑ x ∈ X P ( x ) = 1 \sum_{x\in X}P(x)=1 ∑x∈XP(x)=1-归一化条件。
3.3.2 连续型变量和概率密度函数
连续型随机变量的概率分布用概率密度函数来描述。
⋆ \star ⋆概率密度函数的定义:
如果一个函数 p p p是概率密度函数,必须满足以下3个条件:
(1): p p p的定义域必须是 x x x所有可能状态的集合。
(2): ∀ x ∈ X , p ( x ) ≥ 0. \forall x\in X,p(x)\geq 0. ∀x∈X,p(x)≥0.
(3): ∫ p ( x ) d x = 1 \int p(x)dx=1 ∫p(x)dx=1
概率密度函数 p ( x ) p(x) p(x)并没有直接对特定的状态给出概率,相对的,它给出了落在面积为 δ x \delta x δx的无限小的区域内的概率为 p ( x ) δ x p(x)\delta x p(x)δx.对概率密度函数求积分来获得点击的真实概率质量。
3.4 边缘概率
当知道了一组变量的联合概率分布,想要了解其中一个自己的概率分布,这种定义在子集上的概率分布被称为边缘概率分布。
⋆ \star ⋆离散型随机变量 x , y x,y x,y,已知 P ( x , y ) P(x,y) P(x,y),利用下面的求和法则计算 P ( x ) P(x) P(x):
∀ x ∈ X , P ( X = x ) = ∑ y P ( X = x . Y = y ) \forall x\in X,P(X=x)=\sum_yP(X=x.Y=y) ∀x∈X,P(X=x)=y∑P(X=x.Y=y)
⋆ \star ⋆连续型变量:
p ( x ) = ∫ p ( x , y ) d y p(x)=\int p(x,y)dy p(x)=∫p(x,y)dy
3.5 条件概率
某个事件,在给定其他时间发生时出现的概率。这种概率叫做条件概率。我们讲给定 X = x , Y = y X=x,Y=y X=x,Y=y发生的条件概率记为 P ( Y = y ∣ x = x ) P(Y=y|x=x) P(Y=y∣x=x)。这个条件概率可以通过下面的公式计算:
P ( Y = y ∣ x = x ) = P ( Y = y , X = x ) p ( X = x ) P(Y=y|x=x)=\frac{P(Y=y,X=x)}{p(X=x)} P(Y=y∣x=x)=p(X=x)P(Y=y,X=x)
3.6 条件概率的链式法则
任何多维随机变量的联合概率分布,都可分解成或者只有一个变量的条件概率相乘的形式:
P ( x ( 1 ) , . . . , x ( n ) ) = P ( x ( 1 ) Π i = 1 n P ( x ( i ) ∣ x ( 1 ) , . . . , x ( i − 1 ) ) ) P(x^{(1)},...,x^{(n)})=P(x^{(1)}\Pi^n_{i=1}P(x^{(i)}|x^{(1)},...,x^{(i-1)})) P(x(1),...,x(n))=P(x(1)Πi=1nP(x(i)∣x(1),...,x(i−1)))
这个规则称为链式法则。
3.7 独立性和条件独立性
两个随机变量 x x x和 y y y,如果它们的概率分布可以表示成两个因子的乘积形式,并且一个印子只包含 x x x,另一个因子只包含 y y y,我们就称这两个随机变量是相互独立的。
∀ x ∈ X , y ∈ Y , p ( X = x , Y = y ) = p ( X = x ) p ( Y = y ) \forall x\in X,y\in Y,p(X=x,Y=y)=p(X=x)p(Y=y) ∀x∈X,y∈Y,p(X=x,Y=y)=p(X=x)p(Y=y)
如果关于 x x x和 y y y的条件概率分布对于 z z z的每一个值都可以以写成乘积形式那么这两个随机变量 x x x和 y y y在给定随机变量 z z z时是条件独立的。
∀ x ∈ X , y ∈ Y , z ∈ Z , p ( X = x , Y = y ∣ Z = z ) = p ( X = x ∣ Z = z ) p ( Y = y ∣ Z = z ) \forall x\in X,y\in Y,z\in Z,p(X=x,Y=y|Z=z)=p(X=x|Z=z)p(Y=y|Z=z) ∀x∈X,y∈Y,z∈Z,p(X=x,Y=y∣Z=z)=p(X=x∣Z=z)p(Y=y∣Z=z)
3.8 期望、方差和协方差
- 期望:
函数 f ( x ) f(x) f(x)关于某分布 P ( x ) P(x) P(x)的期望或者期望值是指:当 x x x由 P P P产生, f f f作用于 x x x时, f ( x ) f(x) f(x)额平均值。
⋆ \star ⋆ 离散型随机变量的期望:
E X ∼ p [ f ( x ) ] = ∑ x P ( x ) f ( x ) E_{X\sim p}[f(x)]=\sum_xP(x)f(x) EX∼p[f(x)]=x∑P(x)f(x)
⋆ \star ⋆ 连续型随机变量的期望:
E X ∼ p [ f ( x ) ] = ∫ p ( x ) f ( x ) d x E_{X\sim p}[f(x)]=\int p(x)f(x)dx EX∼p[f(x)]=∫p(x)f(x)dx
期望是线性的:
E X [ α f ( x ) + β g ( x ) ] = α E X [ f ( x ) ] + β E X [ g ( x ) ] E_{X}[\alpha f(x)+\beta g(x)]=\alpha E_{X}[f(x)]+\beta E_{X}[g(x)] EX[αf(x)+βg(x)]=αEX[f(x)]+βEX[g(x)]
其中 α \alpha α和 β \beta β不依赖于 x x x。 - 方差:
衡量的是当我们对 x x x一句他的概率分布进行采样时,随机变量 x x x的函数值会呈现多大的差异:
V a r ( f ( x ) ) = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] Var(f(x))=E[(f(x)-E[f(x)])^2] Var(f(x))=E[(f(x)−E[f(x)])2]
当方差很小时, f ( x ) f(x) f(x)的值形成的簇比较接近它们的期望值。方差的平方根被称为标准差。 - 协方差:
在某种意义上给出了两个变量线性相关的强度以及这些变量的尺度:
C o v ( f ( x ) , g ( x ) ) = E [ ( f ( x ) − E [ f ( x ) ] ) ( g ( x ) − E [ g ( x ) ] ) ] Cov(f(x),g(x))=E[(f(x)-E[f(x)])(g(x)-E[g(x)])] Cov(f(x),g(x))=E[(f(x)−E[f(x)])(g(x)−E[g(x)])]
协方差的绝对值很大,意味着变量值变化很大营切他们同事距离各自的均值很远。
如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。
如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于取得相对较小的值。
⋆ \star ⋆ **相关系数:**将每个变量的贡献归一化,为了只衡量变量的相关性而不受各个变量尺度大小的影响。
⋆ \star ⋆ 协方差和相关系数的关系:
⋆ \star ⋆ 协方差矩阵:随机变量 x ∈ R n x\in R^n x∈Rn的协方差矩阵是一个 n × n n\times n n×n的矩阵,并且满足:
C o v ( x ) i , j = C o v ( x i , x j ) Cov(x)_{i,j}=Cov(x_i,x_j) Cov(x)i,j=Cov(xi,xj)
协方差矩阵的对角元是方差:
C o v ( x i , x i ) = V a r ( x i ) Cov(x_i,x_i)=Var(x_i) Cov(xi,xi)=Var(xi)
3.9 常用概率分布
3.9.1 Bernoulli分布
Bernoulli分布是单个二值随机变量的分布。它由单个参数 Φ ∈ [ 0 , 1 ] \Phi \in [0,1] Φ∈[0,1]控制, Φ \Phi Φ给出了随机变量等于1的概率。它具有如下的一些性质:
P ( X = 1 ) = Φ P(X=1)=\Phi P(X=1)=Φ
P ( X = 0 ) = 1 − Φ P(X=0)=1-\Phi P(X=0)=1−Φ
P ( X = x ) = Φ x ( 1 − Φ ) 1 − x P(X=x)=\Phi ^x(1-\Phi)^{1-x} P(X=x)=Φx(1−Φ)1−x
E X [ x ] = Φ E_X[x]=\Phi EX[x]=Φ
V a r X ( x ) = Φ ( 1 − Φ ) Var_X(x)=\Phi(1-\Phi) VarX(x)=Φ(1−Φ)
3.9.2 Multinoulli分布
M u l t i n o u l l i Multinoulli Multinoulli分布或者范畴分布是指在具有 k k k个不同状态的单个离散型随机变量上的分布,其中 k k k是一个有限值。
M u l t i n o u l l i Multinoulli Multinoulli分布由向量 p ∈ [ 0 , 1 ] k − 1 p\in [0,1]^{k-1} p∈[0,1]k−1参数化。其中每个分量 p i p_i pi表示第 i i i个状态的概率。
M u l t i n o u l l i Multinoulli Multinoulli分布经常表示对象分类的分布。
3.9.3 高斯分布
实数上最常用的分布就是正态分布或者高斯分布:
N ( x ; μ , σ 2 ) = 1 2 π σ 2 e x p ( − 1 2 σ 2 ( x − μ ) 2 ) N(x;\mu ,\sigma ^2)=\sqrt {\frac{1}{2\pi \sigma ^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2) N(x;μ,σ2)=2πσ21exp(−2σ21(x−μ)2)

正态分布由两个参数控制, μ ∈ R \mu \in R μ∈R和 σ ∈ ( 0 , ∞ ) \sigma \in (0,\infty) σ∈(0,∞)。
参数 μ \mu μ给出了中心峰值的坐标,这也是分布的均值: E [ X ] = μ E[X]=\mu E[X]=μ.
分布的标准差用 σ \sigma σ表示,方差用 σ 2 \sigma^2 σ2表示。
一种更高效的参数化分布的方式是使用参数 β ∈ ( 0 , ∞ ) \beta\in (0,\infty) β∈(0,∞),来控制分布的精度: N ( x ; μ , β − 1 ) = β 2 π e x p ( − 1 2 β ( x − μ ) 2 ) . N(x;\mu,\beta^{-1})=\sqrt{\frac{\beta}{2\pi}}exp(-\frac{1}{2}\beta(x-\mu)^2). N(x;μ,β−1)=2πβexp(−21β(x−μ)2).
多维正态分布:它的参数是一个正定对称矩阵 ∑ \sum ∑:
N ( x ; μ , ∑ ) = 1 2 π ) n d e t ( ∑ ) e x p ( − 1 2 ( x − μ ) ⊤ ∑ − 1 ( x − μ ) ) N(x;\mu,\sum)=\sqrt{\frac{1}{2\pi)^n det(\sum)}}exp(-\frac{1}{2}(x-\mu)^{\top}{\sum}^{-1}(x-\mu)) N(x;μ,∑)=2π)ndet(∑)1exp(−21(x−μ)⊤∑−1(x−μ))
参数 μ \mu μ仍然表示分布的均值,只不过现在是向量值。
参数 ∑ \sum ∑给出了分布的协方差矩阵。
当希望对很多不同参数下的概率密度函数多次求值时,协方差矩阵并不是一个很搞笑的参数化分布的方式,因为对概率密度函数求值时,需要对 ∑ \sum ∑求逆。可以使用一个精度矩阵 β \beta β进行替代:
N ( x ; μ , β − 1 ) = d e t ( β ) ( 2 π ) n e x p ( − 1 2 ( x − μ ) ⊤ β ( x − μ ) ) N(x;\mu,\beta^{-1})=\sqrt{\frac{det(\beta)}{(2\pi)^n}}exp(-\frac{1}{2}(x-\mu)^{\top}\beta(x-\mu)) N(x;μ,β−1)=(2π)ndet(β)exp(−21(x−μ)⊤β(x−μ))
我们常把协方差矩阵固定成一个对角矩阵。一个更简单的版本是各向同性高斯分布,它的协方差矩阵是一个标量乘以单位阵。
3.9.4 指数分布和Laplace分布
指数分布:
p ( x ; λ ) = λ 1 x ≥ 0 e x p ( − λ x ) p(x;\lambda)=\lambda 1_{x\geq0}exp(-\lambda x) p(x;λ)=λ1x≥0exp(−λx)
指数分布使用指示函数 1 x ≥ 0 1_{x\geq 0} 1x≥0来使得当 x x x取负值时的概率为零。
Laplace分布:它允许我们在任意一点 μ \mu μ处设置概率质量的峰值
L a p l a c e ( x ; μ , γ ) = 1 2 γ e x p ( − ∣ x − μ ∣ γ ) Laplace(x;\mu,\gamma)=\frac{1}{2\gamma}exp(-\frac{|x-\mu|}{\gamma}) Laplace(x;μ,γ)=2γ1exp(−γ∣x−μ∣)
3.9.5 Dirac分布和经验分布
Dirac delta 函数:概率分布中的所有质量都集中在一个点上
p ( x ) = δ ( x − μ ) p(x)=\delta(x-\mu) p(x)=δ(x−μ)
Dirac delta函数被定义为在除了0以外的所有点的值都为0,但是积分为1。它被称为广义函数,可以把Dirac delta函数想成一系列函数的极限点,这一系列函数把除0以外的所有点的概率密度越变越小。
Dirac分布经常作为经验分布的一个组成部分出现:
p ^ ( x ) = 1 m ∑ i = 1 m δ ( x − x ( i ) ) \hat p(x)=\frac{1}{m}\sum^m_{i=1}\delta(x-x^{(i)}) p^(x)=m1i=1∑mδ(x−x(i))
经验分布将概率密度 1 m \frac{1}{m} m1赋给 m m m个点 x ( 1 ) , . . . , x ( m ) x^{(1)},...,x^{}(m) x(1),...,x(m)中的每一个,这些点是给定的数据集或者采样的集合。只有在定义连续型随机变量的经验分布时,Dirac delta函数才是必要的。
离散型随机变量经验分布可以被定义成一个Multinoulli分布,对于每一个可能的输入,其概率可以简单地设为在训练集上那个输入值的经验频率。
3.9.6 分布的混合
混合分布由一些组件分布构成,每次实验,样本是由哪个组件分布产生的取决于从一个Multinoulli分布中采样的结果:
P ( x ) = ∑ i P ( c = i ) P ( x ∣ c = i ) P(x)=\sum_iP(c=i)P(x|c=i) P(x)=i∑P(c=i)P(x∣c=i)
这里 P ( c ) P(c) P(c)是对各组件的一个Multinoulli分布。
潜变量:不能直接观测到的随机变量。在联合分布中可能和 x x x有关,在这种情况下, P ( x , c ) = P ( x ∣ c ) P ( c ) P(x,c)=P(x|c)P(c) P(x,c)=P(x∣c)P(c)
潜变量的分布 P ( c ) P(c) P(c)以及关联潜变量和观测变量的条件分布 P ( x ∣ c ) P(x|c) P(x∣c),共同决定了分布 P ( x ) P(x) P(x)的形状,尽管描述 P ( x ) P(x) P(x)
时并不需要潜变量。
高斯混合模型:它的组件 P ( x ∣ c = i ) P(x|c=i) P(x∣c=i)是高斯分布。每个组件都有各自的参数,均值 μ ( i ) \mu^{(i)} μ(i)和协方差矩阵 ∑ ( i ) \sum^{(i)} ∑(i)
除了均值和协方差以外,高斯混合模型的参数指明了给每个组件 i i i的先验概率 α i = P ( c = i ) \alpha_i=P(c=i) αi=P(c=i), P ( c ∣ x ) P(c|x) P(c∣x)是后验概率。
高斯混合模型是概率密度的万能近似器:在这种意义下,任何平滑的概率密度都可以用具有足够多组件的高斯混合模型以任意精度来逼近。
3.10 常用函数的有用性质
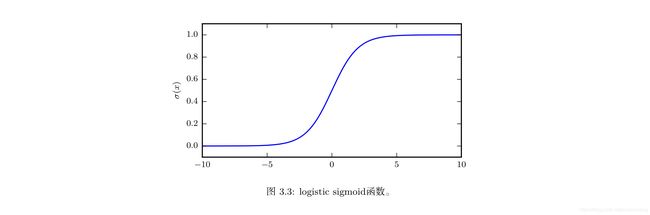
l o g i s t i c logistic logistic s i g m o i d sigmoid sigmoid 函数:
σ ( x ) = 1 1 + e x p ( − x ) \sigma(x)=\frac{1}{1+exp(-x)} σ(x)=1+exp(−x)1
logistic sigmoid 函数通常用来产生Bernoulli分布中的参数 Φ \Phi Φ,因为它的范围是 ( 0 , 1 ) (0,1) (0,1)
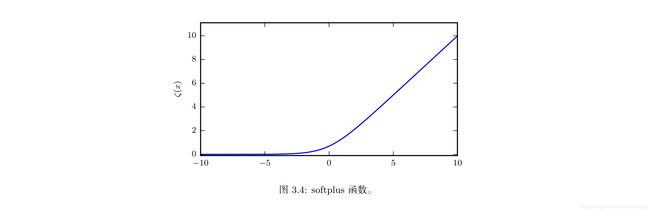
softplus函数:
ζ ( x ) = l o g ( 1 + e x p ( x ) ) \zeta(x)=log(1+exp(x)) ζ(x)=log(1+exp(x))
softplus函数用来产生正态分布的 β \beta β和 δ \delta δ参数,因为它的范围是 ( 0 , ∞ ) (0,\infty) (0,∞).
softplus函数名来源于它是另一个函数的平滑形式,这个函数是:
x + = m a x ( 0 , x ) x^+=max(0,x) x+=max(0,x)
下面的性质很重要:
σ ( x ) = e x p ( x ) e x p ( x ) + e x p ( 0 ) \sigma(x)=\frac{exp(x)}{exp(x)+exp(0)} σ(x)=exp(x)+exp(0)exp(x)
d d x σ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \frac{d}{dx}\sigma(x)=\sigma(x)(1-\sigma(x)) dxdσ(x)=σ(x)(1−σ(x))
1 − σ ( x ) = σ ( − x ) 1-\sigma(x)=\sigma(-x) 1−σ(x)=σ(−x)
l o g σ ( x ) = − ζ ( − x ) log\sigma(x)=-\zeta(-x) logσ(x)=−ζ(−x)
d d x ζ ( x ) = σ ( x ) \frac{d}{dx}\zeta(x)=\sigma(x) dxdζ(x)=σ(x)
∀ x ∈ ( 0 , 1 ) , σ ( − 1 ) ( x ) = l o g ( x 1 − x ) \forall x\in (0,1),\sigma^{(-1)}(x)=log(\frac{x}{1-x}) ∀x∈(0,1),σ(−1)(x)=log(1−xx)
∀ x > 0 , ζ − 1 ( x ) = l o g ( e x p ( x ) − 1 ) \forall x>0,\zeta^{-1}(x)=log(exp(x)-1) ∀x>0,ζ−1(x)=log(exp(x)−1)
ζ ( x ) = ∫ − ∞ x σ ( y ) d y \zeta(x)=\int_{-\infty}^x \sigma(y)dy ζ(x)=∫−∞xσ(y)dy
ζ ( x ) − ζ ( − x ) = x \zeta(x)-\zeta(-x)=x ζ(x)−ζ(−x)=x
3.11 贝叶斯规则
问题:已知 P ( y ∣ x ) P(y|x) P(y∣x)时计算 P ( x ∣ y ) P(x|y) P(x∣y)
如果知道 P ( x ) P(x) P(x),利用贝叶斯规则:
P ( x ∣ y ) = P ( x ) P ( y ∣ x ) P ( y ) P(x|y)=\frac{P(x)P(y|x)}{P(y)} P(x∣y)=P(y)P(x)P(y∣x),其中 P ( y ) = ∑ x P ( y ∣ x ) P ( x ) P(y)=\sum_x P(y|x)P(x) P(y)=∑xP(y∣x)P(x)
3.12 连续型变量的技术细节
1、概率论中的一些重要结果对于离散值成立但对于连续值只能是“几乎处处”成立。
零测度:直观理解为零测度集在度量空间中不占有任何体积。可数多个零测度集的并任然是零测度的。
几乎处处:某个性质如果是几乎处处成立的那么他在整个空间中出了一个测度为零的集合外都是成立的。
2、相互之间有确定性函数关系的连续型随机变量的处理。
3.13 信息论
自信息:一个事件 X = x X=x X=x的自信息:
I ( x ) = − l o g P ( x ) I(x)=-logP(x) I(x)=−logP(x), l o g log log表示自然对数,底数为 e e e.因此我们定义的 I ( x ) I(x) I(x)单位为奈特。一奈特是以 1 e \frac{1}{e} e1的概率观测到一个事件时获得的信息量。自信息只处理单个的输出。
香农熵:对整个概率分布中的不确定性总量进行量化:
H ( x ) = E X ∼ P [ I ( x ) ] = − E X ∼ P [ l o g P ( x ) ] . H(x)=E_{X\sim P}[I(x)]=-E_{X\sim P}[log P(x)]. H(x)=EX∼P[I(x)]=−EX∼P[logP(x)].
也记做: H ( P ) H(P) H(P).一个分布的香农熵是指遵循这个分布的时间所产生的期望信息总量。它给出了一句概率分布 P P P生成的符号进行编码所需的比特数在平均意义上的下界。
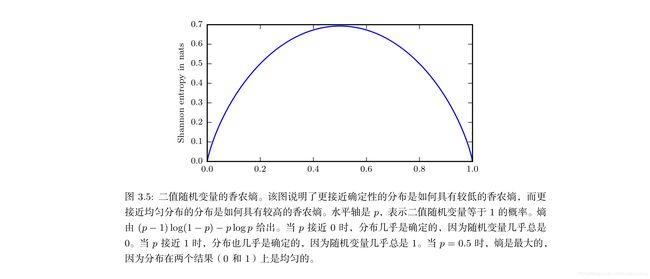
当 x x x是连续的,香农熵被称为微分熵。
K L KL KL散度:同一个随机变量 x x x有两个单独的概率分布 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x),用KL散度来衡量这两个分布的差异:
D K L ( P ∣ ∣ Q ) = E X ∼ P [ l o g P ( x ) Q ( x ) ] = E X ∼ P [ l o g P ( x ) − l o g Q ( x ) ] D_{KL}(P||Q)=E_{X\sim P}[log\frac{P(x)}{Q(x)}]=E_{X\sim P}[logP(x)-logQ(x)] DKL(P∣∣Q)=EX∼P[logQ(x)P(x)]=EX∼P[logP(x)−logQ(x)]
在离散型变量的情况下,KL散度衡量的是:当我们使用一种被设计成能够使得概率分布 Q Q Q产生的消息的长度最小的编码,发送包含由概率分布P产生的符号的消息时,所需要的额外的信息量。
KL散度是非负的。KL散度为0当且仅当P和Q在离散型随机变量的情况下是相同的分布。在连续型变量的情况下是“几乎处处”相同的。
KL散度是非负的并且衡量的是两个分布之间的差异,它经常被用作分布之间的某种距离,但是它不是真正的距离,因为它不是对称的:对于某写P和Q, D K L ( P ∣ ∣ Q ) ≠ D K L ( Q ∣ ∣ P ) D_{KL}(P||Q)\neq D_{KL}(Q||P) DKL(P∣∣Q)=DKL(Q∣∣P)
交叉熵: H ( P , Q ) = H ( P ) + D K L ( P ∣ ∣ Q ) H(P,Q)=H(P)+D_{KL}(P||Q) H(P,Q)=H(P)+DKL(P∣∣Q),它和 K L KL KL散度很像但是缺少左边一项:
H ( P , Q ) = − E X ∼ P l o g Q ( x ) H(P,Q)=-E_{X\sim P}logQ(x) H(P,Q)=−EX∼PlogQ(x),针对 Q Q Q最小化交叉熵等价于最小化 K L KL KL散度,因为 Q Q Q并不参与被省略的那一项。
3.14 结构化概率模型
结构化概率模型(图模型):把概率分布分解成许多因子的乘积形式,而不是使用单一的函数来表示概率分布。用图来表示这种概率分布的分解,称为结构化概率模型。
两种主要的结构化概率模型:有向和无向。两种图模型都使用 G G G,其中图的每个节点对应着一个随机变量,连接两个随机变量的边意味着概率分布可以表示成这两个随机变量之间的直接作用。
有向模型:使用带有有向边的图。它们用条件概率分布来表示分解,有向模型对于分布中每一个随机变量 x i x_i xi都包含一个影响因子,这个组成 x i x_i xi条件概率的影响因子被称为 x i x_i xi的父节点,记为: P a G ( x i ) P_{aG}(x_i) PaG(xi):
p ( x ) = Π i p ( x i ∣ P a G ( x i ) ) p(x)=\Pi_i p(x_i|P_{aG}(x_i)) p(x)=Πip(xi∣PaG(xi))

无向模型:使用带有无向边的图。它们将分解表示成一组函数,这些函数通常不是任何类型的概率分布。 G G G中任何满足两两之间有边连接的顶点的集合被称为团。无向模型中每个团 C ( i ) C^{(i)} C(i)都伴随着一个因子 ϕ ( i ) ( C ( i ) ) \phi^{(i)}(C^{(i)}) ϕ(i)(C(i))。这些因子仅是函数,并不是概率分布。每个因子的输出都必须是非负的。
随机变量的联合概率与所有这些因子的乘积成比例——意味着因子的值越大越有可能性。当然不能保证这种乘积的求和为1,所以我们需要除以一个归一化常数 Z Z Z,来得到归一化的概率分布。归一化常数 Z Z Z被定义为 ϕ \phi ϕ函数乘积的所有状态的求和或积分。概率分布为:
p ( x ) = 1 Z ∏ i ϕ ( i ) ( C ( i ) ) p(x)=\frac{1}{Z}\prod_i\phi^{(i)}(C^{}(i)) p(x)=Z1i∏ϕ(i)(C(i))

第四章 数值计算
4.1 上溢和下溢
- 下溢:一种极具毁灭性的舍入误差。当接近为0的数被四舍五入为0时发生下溢。
- 上溢:一种极具破坏力的数值错误形式。当大量级的数被近似为 ∞ \infty ∞或 − ∞ -\infty −∞时发生上溢。
- softmax函数:
s o f t m a x ( X ) i = e x p ( x i ) ∑ i = 1 n e x p ( x j ) softmax(X)_i=\frac{exp(x_i)}{\sum ^n_{i=1}exp(x_j)} softmax(X)i=∑i=1nexp(xj)exp(xi)
softmax函数经常用于预测与Multinoulli分布相关联的概率。
4.2 病态条件
- 条件数:表征函数相对于输入的微小变化而变化的快慢程度。
输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的,因为输入中的舍入误差可能导致输出的巨大变化。
考虑函数 f ( x ) = A − 1 x f(x)=A^{-1}x f(x)=A−1x当 A ∈ R n × n A\in R^{n\times n} A∈Rn×n具有特征值分解时,其条件数为:
m a x i , j ∣ λ i λ j ∣ max_{i,j}\vert \frac{\lambda_i}{\lambda_j}\vert maxi,j∣λjλi∣
这是最大和最小特征值的模之比
4.3 基于梯度的优化方法
- 优化:改变 x x x以最小化或最大化某个函数 f ( x ) f(x) f(x)的任务。
- 目标函数(准则):把要最小化或者最大化的函数成为目标函数。
- 代价函数(损失函数、误差函数):当我们对其最小化时我们也称之为代价函数。
- x ∗ = a r g m i n f ( x ) x^*=arg min f(x) x∗=argminf(x), ∗ * ∗表示最小化或者最大化函数的 x x x值。
- 梯度下降:
函数 f ( x ) f(x) f(x)的导数 f ′ ( x ) f^{\prime}(x) f′(x)代表 f ( x ) f(x) f(x)在点 x x x处的斜率,它表明如何缩放输入的小变化才能在输出获得相应的变化: f ( x + ϵ ) ≈ f ( x ) + f ′ ( x ) ϵ f(x+\epsilon)\approx f(x)+f^{\prime}(x)\epsilon f(x+ϵ)≈f(x)+f′(x)ϵ。
对于足够小的 ϵ \epsilon ϵ来说, f ( x − ϵ s i g n ( f ′ ( x ) ) ) f(x-\epsilon sign(f^{\prime}(x))) f(x−ϵsign(f′(x)))是比 f ( x ) f(x) f(x)小的。因此,我们可以将 x x x往导数的反方向移动一小步来减小 f ( x ) f(x) f(x)。这种技术被称为梯度下降.

- 最速下降法(梯度下降):
梯度:相对一个向量求导的导数: f f f的导数是包含搜又偏导数的向量。记为: ▽ x f ( x ) \bigtriangledown_x f(x) ▽xf(x),梯度的第 i i i个元素是 f f f关于 x i x_i xi的偏导数。
方向导数:在 u u u放向的方向导数是函数 f f f在 u u u方向的斜率。方向导数是函数 f ( x + α u ) f(x+\alpha u) f(x+αu)关于 α \alpha α的导数(在 α = 0 \alpha =0 α=0时取得)。使用链式法则,当 α = 0 \alpha =0 α=0时, ∂ ∂ α f ( x + α u ) = u ⊤ ▽ x f ( x ) \frac{\partial}{\partial\alpha}f(x+\alpha u)=u^{\top}\bigtriangledown_x f(x) ∂α∂f(x+αu)=u⊤▽xf(x)
为了最小化 f f f,我们需要找到使得 f f f下降得最快的方向。计算方向导数:
m i n u , u ⊤ u = 1 u ⊤ ▽ x f ( x ) min_{u,u^{\top} u=1}u^{\top}\bigtriangledown_x f(x) minu,u⊤u=1u⊤▽xf(x)
= m i n u , u ⊤ u = 1 ∣ ∣ u ∣ ∣ 2 ▽ x f ( x ) ∣ ∣ 2 c o s θ =min_{u,u^{\top} u=1}\vert\vert u \vert\vert_2\bigtriangledown _xf(x)\vert\vert_2cos\theta =minu,u⊤u=1∣∣u∣∣2▽xf(x)∣∣2cosθ