树链剖分详解
树链剖分,正如其名,这个算法的主要思想就是 把“树”“剖分”成“链”
那怎么实现以及它的作用是什么呢,以洛谷上的模板题为例子:
已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
很明显,我们需要维护的是树上的路径,对于第一个操作,我们可以用倍增来做,但是带上修改的话,倍增就很难做了(没准有些神犇真的可以做呢),于是,我们就用到了树链剖分,树链剖分的主要做法就是先把这颗树拆成一条一条链,那么对于每一条链,我们可以用线段树来维护,那么怎么拆这颗树呢,这才是树链剖分的要点。
前置概念:重儿子——一个节点的所有儿子中子树最大的儿子
求重儿子的话遍历一下整棵树就好了。
代码:
void dfs_getson(int x)
{
size[x]=1;//初始化树的大小
for(int i=first[x];i;i=e[i].next)
{
int y=e[i].y;
if(y==fa[x])continue;//不能往回走
fa[y]=x;deep[y]=deep[x]+1;//记录父亲和深度
dfs_getson(y);
size[x]+=size[y];
if(size[y]>size[son[x]])son[x]=y;//更新重儿子
}
}
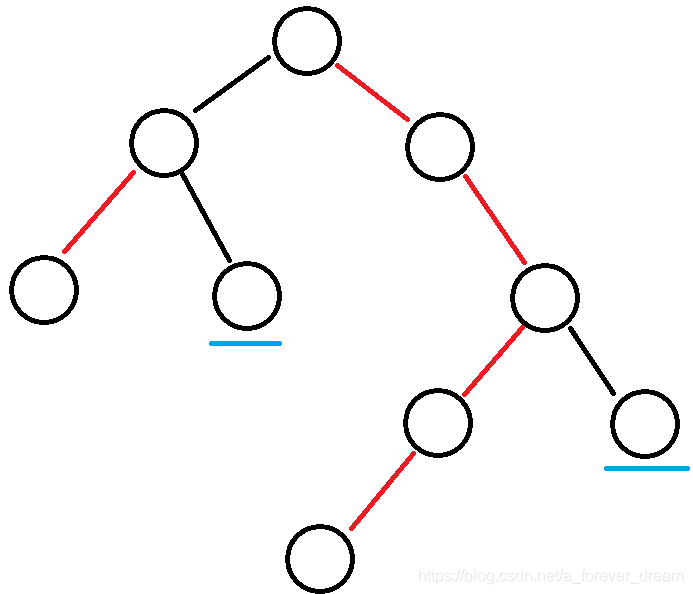
那我们得到了重儿子之后有什么用呢?这里又要引出一个概念:重链——由重儿子组成的链,比如有这么一棵树:
这棵树的重链就长这个样子了,那两个下面有蓝线的点自己就是一条重链
问题又来了,重链有什么用?
下面这个性质就是树链剖分的核心了:从任意一个点出发,到根节点的路径上不会经过超过 log(n) 条重链。换句话说,不会经过超过 log(n) 条轻边。
证明:我们发现,对于 x 的一个轻儿子 y,y 的子树大小肯定是小于 x 的子树大小的一半的。那么我们考虑极端情况,从根节点往任意一个节点走,设 size 为当前点的子树大小,那么每经过一条轻边,size就会除以2,因为 size 是不可能小于 0 的,所以最多经过 log(n) 条轻边。
有了这个性质之后,接下来请出 dfs 序——我们考虑造出这颗树的 dfs 序,但是 dfs 的时候优先往重儿子那里走,那么就可以得到一个性质:一条重链上的 dfs 序是连续的,这样我们就可以用线段树来维护这一段的信息了。
dfs的代码如下:
void dfs_rewrite(int x,int tp)//当前点以及当前点所在重链的顶端
{
top[x]=tp;//更新每个点所在的重链的顶端
now[x]=++tot;//得到每个点的dfs序(新编号)
past[tot]=x;//记录每个新编号对应的原来的点
if(son[x])dfs_rewrite(son[x],tp);//优先往重儿子那里走
for(int i=first[x];i;i=e[i].next)
{
int y=e[i].y;
if(y!=son[x]&&y!=fa[x])dfs_rewrite(y,y);
}
ctr[x]=tot;//作用后面会讲
}然后再建一颗线段树来维护他们:
void buildtree(int x,int y)
{
len++;
tree[len].l=x;
tree[len].r=y;
tree[len].late=0;
if(x==y)
{
tree[len].zuo=tree[len].you=-1;
tree[len].c=a[past[x]];//x是新编号,past[x]才是原来的编号,叶子的值应该是a[原来的编号]
}
else
{
int noww=len,mid=x+y>>1;
tree[noww].zuo=len+1;buildtree(x,mid);
tree[noww].you=len+1;buildtree(mid+1,y);
tree[noww].c=tree[tree[noww].zuo].c+tree[tree[noww].you].c;
}
}然后我们现在考虑怎么利用这些结构来解决上面的问题。
要求x到y的路径,也就是找最近公共祖先的问题。那么只需要每次让所在重链的顶端的深度更大的往上跳,直到它们在同一条重链上停止即可。
为什么呢?为什么每次跳得不是深度更大的节点而是所在重链的顶端的深度更大的往上跳?
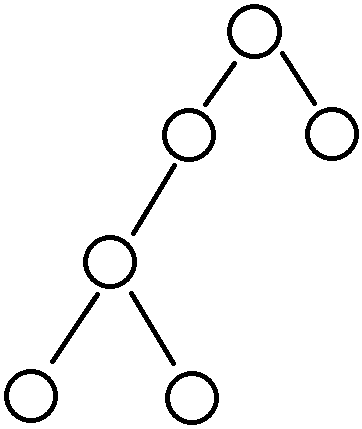
因为,如果先跳深度更大的,有可能会跳过头,比如,有这么一棵树:
显然的,重链有三条:
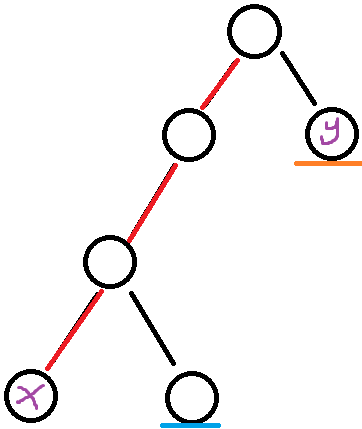
假如x和y是这两个点:
那么显然的,问题出现了,假如深度大的先跳,那么x会先跳,然后……就没有然后了,x会跳到不知道哪里去……
但如果先跳y的话,他会先跳到自己,然后再跳到他的父亲——根节点,然后他们就在同一条重链上了。
所以,应该先跳top深度大的点,那么我们就可以在跳的时候顺便搞一下路径上的节点,然后就ok了。
代码如下:
void change_xtoy()//修改
{
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
while(top[x]!=top[y])//假如不在同一条重链上
{
if(deep[top[x]]>deep[top[y])swap(x,y);//优先跳top深度更深的,将它存在y中
change(1,now[top[y]],now[y],z);//修改路径上的点的值
y=fa[top[y]];//往上跳
}
if(deep[x]>deep[y])swap(x,y);
change(1,now[x],now[y],z);//当他们在同一条重链上时,最后修改一下x~y路径上的点
}
void getsum_xtoy()//查询,与修改基本相同
{
int x,y;
scanf("%d %d",&x,&y);
ll ans=0;
while(top[x]!=top[y])
{
if(deep[top[x]]>deep[top[y]])swap(x,y);
ans=(ans+getsum(1,now[top[y]],now[y]))%p;
y=fa[top[y]];
}
if(deep[x]>deep[y])swap(x,y);
ans+=getsum(1,now[x],now[y]);
printf("%lld\n",ans%p);
}然后还剩下一个问题,子树怎么办?
因为以任意一个点作为根,它的子树内的点的 dfs 序都是连续的,所以我们只需要记录以每个节点为根的子树中新编号最大的那个节点的新编号即可,自己的新编号到最大的编号就是以自己为根的子树的新编号的范围。代码如下:
void change_sontree()
{
int x,y;
scanf("%d %d",&x,&y);
change(1,now[x],ctr[x],y);//因为一颗子树的编号是连续的,所以直接修改即可(ctr前面有)
}
void getsum_sontree()
{
int x;
scanf("%d",&x);
printf("%lld\n",getsum(1,now[x],ctr[x])%p);//基本同上
}完整代码如下:
#include
#include
#define ll long long
#define maxn 200010
int n,m,root,p,len=0;
struct node{int x,y,next;};
node e[200010];
int a[maxn];
int first[maxn];
void buildroad(int x,int y)//邻接表建边
{
len++;
e[len].x=x;
e[len].y=y;
e[len].next=first[x];
first[x]=len;
}
int deep[maxn],size[maxn],son[maxn],fa[maxn];
void dfs_getson(int x)
{
size[x]=1;//初始化树的大小
for(int i=first[x];i;i=e[i].next)
{
int y=e[i].y;
if(y==fa[x])continue;//不能往回走
fa[y]=x;deep[y]=deep[x]+1;//记录父亲和深度
dfs_getson(y);
size[x]+=size[y];
if(size[y]>size[son[x]])son[x]=y;//更新重儿子
}
}
int now[maxn],tot=0,top[maxn],past[maxn],ctr[maxn];
void dfs_rewrite(int x,int tp)//当前点以及当前点所在重链的顶端
{
top[x]=tp;//更新每个点所在的重链的顶端
now[x]=++tot;//得到每个点的新编号
past[tot]=x;//记录每个新编号原来是哪个点
if(son[x])dfs_rewrite(son[x],tp);//优先往重儿子那里走
for(int i=first[x];i;i=e[i].next)
{
int y=e[i].y;
if(y!=son[x]&&y!=fa[x])dfs_rewrite(y,y);
}
ctr[x]=tot;//记录以x为根的子树的新编号中最大的那个,子树的范围就是now[x]~ctr[x]
}
struct nod{int l,r,zuo,you;ll c,late;};
nod tree[200010];
void buildtree(int x,int y)//线段树
{
len++;
tree[len].l=x;
tree[len].r=y;
tree[len].late=0;
if(x==y)
{
tree[len].zuo=tree[len].you=-1;
tree[len].c=a[past[x]];//x是新编号,past[x]才是原来的编号,叶子的值应该是a[原来的编号]
}
else
{
int noww=len,mid=x+y>>1;
tree[noww].zuo=len+1;buildtree(x,mid);
tree[noww].you=len+1;buildtree(mid+1,y);
tree[noww].c=tree[tree[noww].zuo].c+tree[tree[noww].you].c;
}
}
void give(int x)
{
if(tree[x].late)
{
tree[x].c+=tree[x].late*(tree[x].r-tree[x].l+1);
int zuo=tree[x].zuo,you=tree[x].you;
if(zuo!=-1)tree[zuo].late+=tree[x].late,tree[you].late+=tree[x].late;
tree[x].late=0;
}
}
void change(int noww,int x,int y,int z)
{
if(tree[noww].l==x&&tree[noww].r==y)
{
tree[noww].late+=z;
give(noww);return;
}
give(noww);
int zuo=tree[noww].zuo,you=tree[noww].you;
int mid=tree[noww].l+tree[noww].r>>1;
if(y<=mid)change(zuo,x,y,z);
else if(x>=mid+1)change(you,x,y,z);
else change(zuo,x,mid,z),change(you,mid+1,y,z);
tree[noww].c+=(y-x+1)*z;
}
ll getsum(int noww,int x,int y)
{
give(noww);
if(tree[noww].l==x&&tree[noww].r==y)return tree[noww].c;
int zuo=tree[noww].zuo,you=tree[noww].you;
int mid=tree[noww].l+tree[noww].r>>1;
if(y<=mid)return getsum(zuo,x,y);
else if(x>=mid+1)return getsum(you,x,y);
else return getsum(zuo,x,mid)+getsum(you,mid+1,y);
}
void swap(int &x,int &y){int t=x;x=y;y=t;}
void change_xtoy()
{
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
while(top[x]!=top[y])//假如不在同一条重链上
{
if(deep[top[x]]>deep[top[y])swap(x,y);//优先跳top深度更深的,将它存在y中
change(1,now[top[y]],now[y],z);//修改路径上的点的值
y=fa[top[y]];//往上跳
}
if(deep[x]>deep[y])swap(x,y);
change(1,now[x],now[y],z);//当他们在同一条重链上时,最后修改一下x~y路径上的点
}
void getsum_xtoy()//基本同上
{
int x,y;
scanf("%d %d",&x,&y);
ll ans=0;
while(top[x]!=top[y])
{
if(deep[top[x]]>deep[top[y]])swap(x,y);
ans=(ans+getsum(1,now[top[y]],now[y]))%p;
y=fa[top[y]];
}
if(deep[x]>deep[y])swap(x,y);
ans+=getsum(1,now[x],now[y]);
printf("%lld\n",ans%p);
}
void change_sontree()
{
int x,y;
scanf("%d %d",&x,&y);
change(1,now[x],ctr[x],y);//因为一颗子树的编号是连续的,所以直接修改即可
}
void getsum_sontree()
{
int x;
scanf("%d",&x);
printf("%lld\n",getsum(1,now[x],ctr[x])%p);//基本与修改相同 基本同上
}
int main()//主程序。。可读性挺好的。。应该不用注释了吧
{
scanf("%d %d %d %d",&n,&m,&root,&p);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i