分位数映射数据后处理-Quantile Mapping后处理 (R语言)
统计后处理器基本上是统计模型,将观察到的关注变量与从气象或水文模型的直接模型输出(DMO)导出的适当预测变量相关联。统计后处理的重要性早已在气象预报中得到认可。早期的工作包括完善的预测(perfect prognosis),模型输出统计(MOS)和模拟方法(analog method)等模型。 近年来,已经提出了许多其他后处理方法,包括秩直方图校准(rank histogram calibration),分位数映射(quantile mapping,QM)和集成预处理器(ensemble preprocessor, EPP)。几种基于贝叶斯定理的模型已被研发了,以将先前的气候学信息与实时预测相结合,例如输出的贝叶斯处理器(Bayesian processor of output, BPO),预测的贝叶斯处理器(Bayesian processor of forecast, BPF)和集合贝叶斯处理器(Bayesian processor of ensemble, BPE)。 同时,也存在多种基于回归的模型,包括集成模型输出统计(EMOS),逻辑回归(logistics regress, LR),分位数回归(quantile regression, QR)和逐成员方法(member-by-member approach)。今天,介绍一种简单的后处理方法,分位数映射(Quantile Mapping)数据后处理方法。
1. 定义
分位数映射后处理,也叫分位数与分位数转换,或者累积分布函数匹配(CDF),是一种简单的后处理方法,具体是根据观测值的CDF去校正预测值的CDF。在实施QM过程中,就是把每个预报的值映射到观测值的CDF上对应的分位数。
下面引用Piani的一篇文章里的图,(Piani C, Statistical bias correction for daily precipitation in regional climate models over Europe. Theor Appl Climatol 2010,99:187–192)
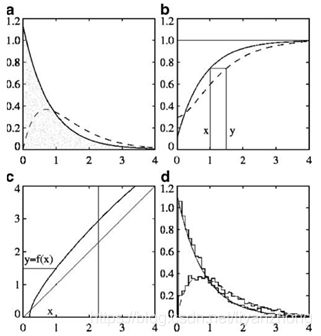
图a中是观测(虚线)和模拟(实线)降水的pdf,图b是根据图a绘制的cdf,实施过程就是在b图中找出所有模拟x值对应cdf值,然后找到与cdf之对应相等的观测值x,比如图b中模拟值x=1时,对应cdf相等的观测值的y=1.5,以此类推,获取无数对的x,y时,就可以画出来图c的映射图了。这样根据映射图,就可以把模拟值的所有值映射到观测值的分布上了,通过对随机数据测试(图d),发现对模拟值(实线直方图)矫正,获取到了校正后的值,发现校正后值都分布在了理论观测值线附近。
简单图例如下;
图2 分位数映射方法示意图(a),不同QM方法示意图(b)
2.R语言代码
理解了原理后,真正的实施就需要借助编程语言实现。幸运的是别人已经把这个方法写好,并且把代码,测试数据都放到了R语言包网上,供大家学习。包Qmap下载地址:https://cran.r-project.org/。下载后,在R软件中安装就可以使用了,根据测试数据和说明书,测试如下:
install.packages('qmap')#下载并安装包
library(qmap) #引用安装包
sqrtquant<-function(x,qstep=0.01)
{
qq=quantile(x,prob=seq(0,1,by=qstep))
sqrt(qq)
}
data(obsprecip) #加载数据
data(modprecip) #加载数据
#1.拟合的分布为berngamma
qm.gamma.fit=fitQmapDIST(obsprecip[,1],modprecip[,1],distr = "berngamma",qstep = 0.001)
qm.gamma =doQmapDIST(modprecip[,1],qm.fit)
plot(sqrtquant(modprecip[,1]), sqrtquant(obsprecip[,1]))
lines(sqrtquant(modprecip[,1]), sqrtquant(qm),col="red")
#2.拟合的分布为bernlnorm
qm.lnorm.fit=fitQmapDIST(obsprecip[,1],modprecip[,1],distr = "bernlnorm",qstep = 0.001)
qm.lnorm =doQmapDIST(modprecip[,1],qm.lnorm.fit)
lines(sqrtquant(modprecip[,1]),sqrtquant(qm.lnorm),col="blue")
#3.拟合的分布为weibu
qm.weibu.fit=fitQmapDIST(obsprecip[,1],modprecip[,1],distr = 'bernweibull',qstep=0.001)
qm.weibu=doQmapDIST(modprecip[,1],qm.weibu.fit)
lines( sqrtquant(modprecip[,1]), sqrtquant(qm.weibu),col="green")
#4.拟合的分布为weibu
qm.exp.fit=fitQmapDIST(sqrt(obsprecip[,1]),sqrt(modprecip[,1]), distr="bernexp",qstep=0.001 )
qm.exp=doQmapDIST(sqrt(modprecip[,1]), qm.exp.fit)^2
lines(sqrtquant(modprecip[,1]),sqrtquant(qm.exp),col="orange")
#5.添加图例
legend("topleft",legend = c("berngamma","bernlnorm","bernweibull","bernexp"), lty =1, col=c("red","blue","green","orange") )
结果如图2b所示。
4.QM的不足
然而,QM作为一个非条件的方法,它不需要保留预测值与观测值数据对的关联性。所以,有时候QM可能会对原始数据的思路是错误的,从而导致结果并不如条件方法不满意。此外,Zhao等做了深入研究,发现QM适合对GCM降水进行后处理。他们发现尽管QM能够矫正偏差,但是它并不能保证可靠性和预测的连续性(连续性是指至少与气候学预测一样的性能)。这个原因就是由于QM不能很好的考虑原始模拟值和观测值的相关性。基于此,赵等得出结论说QM并非十分适合后处理,因为它会受到偏差和可信度、连续性的双重影响。