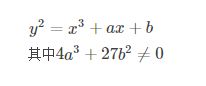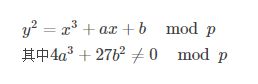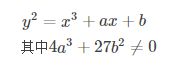【我的区块链之路】- go实现区块链中常见的各类算法
【转载请标明出处】https://blog.csdn.net/qq_25870633/article/details/82900508
咳咳,为什么要出这一篇文章呢?首先,这段时间本人在找工作,然后被问到了各类算法的底层细节,有些确实很懵逼。这里做个总结,也顺便给大家归纳归纳一下!
上主题:
椭圆曲线加密:
我们先来说一说最常用的 ECC 吧,ECC 就是 Elliptic Curve Cryptography 的缩写。那么,在说椭圆曲线加密之前,我们来说一说什么是椭圆曲线?
中学的时候我们学过圆锥曲线,比如椭圆、双曲线和抛物线。因为描述这些曲线的方程都是二次方程,圆锥曲线又被称为二次曲线。而椭圆曲线是则是由三次方程描述的一些曲线。更准确地说,椭圆曲线是由下面的方程描述的曲线:
需要注意的是,椭圆曲线之所以叫“椭圆曲线”,是因为其曲线方程跟利用微积分计算椭圆周长的公式相似。实际上它的图像跟椭圆完全不搭边。
如椭圆曲线 y^2=x^3−x+1 的图像:
【注意】椭圆曲线有这样的两个性质:
- 关于X轴对称
- 画一条直线跟椭圆曲线相交,它们最多有三个交点
椭圆曲线上的运算
由于椭圆曲线加密进行的运算实际上都是在椭圆曲线上进行的,必须注意的是,这里把这些运算称为“加法”和“乘法”仅仅是方便描述,他们跟平时认知的加法和乘法完全是两码事,完全可以给他们取其它名字(比如”乘法“和”幂运算“等)。总之就是规定,规定,规定(重要的事说三遍)
-
首先定义坐标系中距离X轴无穷远点为椭圆曲线上的一个特殊点,称为0点。
那么此时上述第二条性质可以加强为:过曲线上任意两点(可重合)的直线必定与曲线相交于第三点。 -
然后定义椭圆曲线上点的加法。设椭圆曲线上有两点,A和B点,那么作过这两点的直线与该曲线相交于第三点(C点),然后关于X轴对称得到D点,则D为这两个点的和,记作D=A+B (注意: 这仅仅是规定)。很明显,D点也在该曲线上。所以椭圆曲线上两点之和也是曲线上的点。
特别地,如果两点重合,则作椭圆曲线在A点处的切线,与曲线相交于第二点(B点),然后关于X轴对称得到C点,则C点为A点与自身的和,记作 C = 2A。
加法,我们可以得到以下结论:
-
A+B = B+A
也就是椭圆曲线上的加法满足交换律。 -
A+0 = A
因为0点是无穷远点,所以过A点与0点的直线是垂直于X轴的,它与曲线相交于另一点B点,那么B点关于X轴对称的点就是A点,即A点为A点和0点之和。(这里其实是 A+0 = 过A和0的第三点B的对称点A, 所以 A+0=A)
然后在加法的基础上,定义椭圆曲线上点的乘法。
乘法:(下列的也是一种规定,是规定)
设P是椭圆曲线上的一个点,那么正整数k乘以点P的结果由下面的式子定义,注意式子中的加法是上面提到的椭圆曲线上点的加法:
1∗P=P1
2∗P=P+P
3∗P=2∗P+P
…
k∗P=(k−1)∗P+P
乘法满足以下性质:
对于任意正整数k和j,有
k∗(j∗P) = (kj)∗P = (jk)∗P = j∗(k∗P)
知道公钥反推私钥:
k 为正整数,P 是椭圆曲线上的点(称为基点),已知 k∗P 和 P,计算 k
进一步为:
k 为正整数,P 是椭圆曲线上的点,已知 P^k 和 P,计算 k = logP P^k
以上,是复杂度很高的操作,公钥反推私钥很难求 (在椭圆曲线算法中很难求)
【注意】:
密码学中,并不能使用上面介绍的实数域上的椭圆曲线。因为:
1. 实数域上的椭圆曲线是连续的,有无限个点,密码学要求有限点。
2. 实数域上的椭圆曲线的运算有误差,不精确。密码学要求精确。
所以我们需要引入有限域上的椭圆曲线。
有限域上的椭圆曲线:
所谓有限域上的椭圆曲线,简单来说就是满足下面式子要求的曲线(x, y, a, b都是小于素数【也即是质数】p的 非负整数):
对比一下原先的椭圆曲线的方程:
可以看到这个只是对原式进行了简单的取模处理而已。
按数论定义,有限域GF(p)指给定某个质数p,由0、1、2......p-1共p个元素组成的整数集合。且方程的坐标点满足了在有限域中定义的加减乘除运算的结果也应该是在域中。
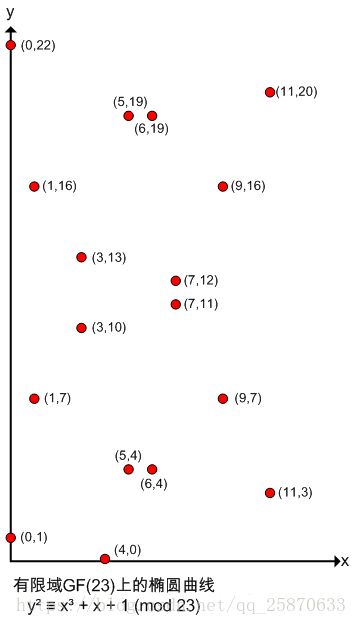
假设椭圆曲线为 y² = x³ + x + 1,其在有限域GF(23)上时,写作:
y² ≡ x³ + x + 1 (mod 23)
此时,椭圆曲线不再是一条光滑曲线,而是一些不连续的点,如以点(1,7)为例,7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此还有如下点:
(0,1) (0,22)
(1,7) (1,16)
(3,10) (3,13)
(4,0)
(5,4) (5,19)
(6,4) (6,19)
(7,11) (7,12)
(9,7) (9,16)
(11,3) (11,20)
等等。
另外,如果P(x,y)为椭圆曲线上的点,则-P即(x,-y)也为椭圆曲线上的点。如点P(0,1),-P=(0,-1)=(0,22)也为椭圆曲线上的点。看图:(该图的点全部以 y = 23/2 对称)并不代表着关于某水平线对称哦,参考:https://www.cnblogs.com/X-knight/p/9153209.html
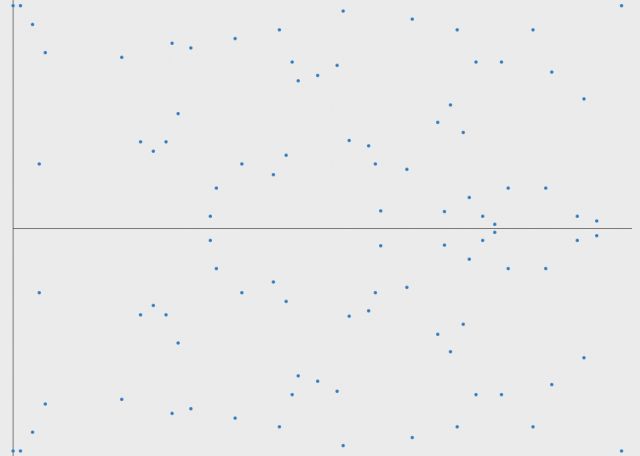
又如下图是椭圆曲线 y² = x³−x+1 对素数97取模后的图像:
原本连续光滑的曲线变成了离散的点,基本已经面目全非了,但是依然可以看到它是关于某条水平直线(y= 97/2)对称的。而且上面定义的椭圆曲线的加法仍然可用(当然乘法也可以)。
【注意】:密码学中有限域上的椭圆曲线一般有两种,一种是定义在以素数p为模的整数域GF(p),也就是上面介绍的;另一种则是定义在特征为 2 的伽罗瓦域 GF(2^m)上。
好了我们下面来看看,逼逼了这么久我们到底是要做什么?
用生成的私钥 + 椭圆曲线 求 公钥的过程就是计算xG的坐标的过程
计算 xG 就是 【私钥 * 基点 = 公钥】
相关公式如下:
有限域GF(p)上的椭圆曲线 y² = x³ + ax + b,若P(Xp, Yp), Q(Xq, Yq),且P≠-Q,则R(Xr,Yr) = P+Q 由如下规则确定:
Xr = (λ² - Xp - Xq) mod p
Yr = (λ(Xp - Xr) - Yp) mod p
其中【公式 1】 λ = (Yq - Yp)/(Xq - Xp) mod p(若P≠Q), 【公式 2】 λ = (3Xp² + a)/2Yp mod p(若P=Q)
因此,有限域GF(23)上的椭圆曲线 y² ≡ x³ + x + 1 (mod 23),假设以(0,1)为G点,计算2G、3G、4G...xG等等,方法如下:
计算2G:
2G = G + G ,所以用 【公式 2】求 λ
λ = (3x0² + 1)/2x1 mod 23 = (1/2) mod 23 = 12
Xr = (12² - 0 - 0) mod 23 = 6
Yr = (12(0 - 6) - 1) mod 23 = 19
即2G为点(6,19)
计算3G:
3G = G + 2G,即(0,1) + (6,19),用【公式 1】求 λ
λ = (19 - 1)/(6 - 0) mod 23 = 3
Xr = (3² - 0 - 6) mod 23 = 3
Yr = (3(0 - 3) - 1) mod 23 = 13
即3G为点(3, 13)
同理计算4G、5G...xG,分布如下图:

所以,上述就是在说,我们如何根据 提前生成好的私钥 X (私钥 可以是有某种随机算法求出来的一个 数字) 和 选定的椭圆曲线 (如:Curve25519,prime256v1,secp256k1)(以上曲线均为有限质数域下的椭圆曲线,表现为 离散的点,根据 y = 质数P/2 水平线对称),求出 公式 XG 点的 坐标 (x ,y) 既是组成公钥的 x 和 y。(其中 G 为选好的椭圆曲线上的基点,即 (x,y) == (0, 0)求出来的曲线上的坐标点,XG 也是曲线上的一点。
实际应用中,我们并不需要关心椭圆曲线的众多参数如何选取(要选对参数 a, b 对于普通使用者来说并不现实),只要从密码学家们精心挑选的一堆曲线中选择一个就行了。一般来说曲线Curve25519,prime256v1是比较常用的,比特币选择secp256k1则是有自己的考量
建立基于椭圆曲线的加密机制,需要找到类似RSA质因子分解或其他求离散对数这样的难题。而椭圆曲线上的已知G和xG求x,是非常困难的(为什么呢?请看计算出XG的步骤就知道的,每一步的 λ 都是不一样的),此即为椭圆曲线上的的离散对数问题。此处x即为私钥,xG即为公钥。
椭圆曲线加密算法原理如下:
设私钥、公钥分别为k、Y,即Y = kG,其中G为基点。
公钥加密:
选择随机数r,将消息M生成密文C,该密文是一个点对,即:
C = {rG, M+rY},其中Y为公钥
私钥解密:
M + rY - k(rG) = M + r(kG) - k(rG) = M
其中k、Y分别为私钥、公钥。
椭圆曲线签名算法原理
椭圆曲线签名算法,即 ECDSA。
设私钥、公钥分别为k、Y,即 Y = kG,其中G为G点。
私钥签名:
1、选择随机数 r,计算点 rG(x, y)。
2、根据随机数r、消息M的哈希h、私钥 k,计算 s = (h + kx)/r。
3、将消息M、和 签名{rG, s}发给接收方。
公钥验证签名:
1、接收方收到消息M、以及签名{rG=(x,y), s}。
2、根据消息求哈希h。
3、使用发送方公钥K计算:hG/s + xY/s,并与rG比较,如相等即验签成功。
原理如下:
hG/s + xY/s = hG/s + x(kG)/s = (h+xk)G/s
= r(h+xk)G / (h+kx) = rG
详细可以参考:https://www.cnblogs.com/X-knight/p/9153209.html
Diffie–Hellman密钥交换 (DH)
Diffie–Hellman密钥交换(以下简称DH)是用于双方在可能被窃听环境下安全交换密钥的一种方法。
算法的安全性是由上面提到的离散对数难题保证。
具体算法流程如下:
- 小红和小明约定 p 和 g 的值
- 小红生成私钥 x,计算 g^x mod p 作为 公钥 公布出去
- 小明生成私钥 y,计算 g^y mod p 作为 公钥 公布出去
- 小红得知 g^y mod p后,计算
s = (g^y mod p)^x mod p = (g^y)^x mod p = g^xy mod p
- 小明得到gxmodpgxmodp后,计算
s = (g^x mod p)^y mod p = (g^x)^y mod p = g^xy mod p
- 双方都得到了相同的密钥的ss,交换完毕
上面的流程中,x 和 y 始终由两人自行保管的,第三方窃听得到的只有 p、g、g^x mod p和 g^y mod p这几个值。
上面说过,离散对数是很难算的,所以第三方不能由这些信息计算出 x 或 y,也就没办法计算出密钥 s 了
基于椭圆曲线的DH密钥交换(ECDH)
ECDH跟DH的流程基本是一致的。
- 小红和小明约定使用某条椭圆曲线(包括曲线参数,有限域参数以及基点P等)
- 小红生成私钥 x,计算 x∗P 作为公钥公布出去
- 小明生成私钥 y,计算 y∗P 作为公钥公布出去
- 小红得知 y∗P 后,计算
s = x∗(y∗P) = xy∗P
- 小明得到x∗Px∗P后,计算
s = y∗(x∗P) = yx∗P
- 双方都得到了相同的密钥的ss,交换完毕
由于计算椭圆曲线上的离散对数是很难的,所以第三方没办法在只知道 x∗P 和 y∗P 的情况下计算出 x 或 y 的值。好了,下面我们来看看椭圆曲线的 go 代码实现吧。【主要为 go 原生的crypto/elliptic和crypto/ecdsa包下的代码分析】
如代码:
/**
曲线接口
库引用路径: crypto/elliptic
代码所在文件路径:src/crypto/elliptic/elliptic.go
*/
type Curve interface {
// 获取椭圆曲线参数
Params() *CurveParams
// 某点是否在曲线上
IsOnCurve(x, y *big.Int) bool
// 加法 (x1,y1) + (x2,y2)
Add(x1, y1, x2, y2 *big.Int) (x, y *big.Int)
// 二倍运算 2*(x,y)
Double(x1, y1 *big.Int) (x, y *big.Int)
// 即乘法 k*(Bx,By)
ScalarMult(x1, y1 *big.Int, k []byte) (x, y *big.Int)
// 即 k*G 其中G 为基点.
ScalarBaseMult(k []byte) (x, y *big.Int)
}上述代码是操作曲线 实现对象的,主要定义了判断曲线上的点,返回曲线的基本参数 (P, n, b,Gx,Gy,BitSize, Name),及曲线上点的加法和乘法运算。
我们再看看,CurveParams 曲线的主要组成参数都是些什么:【其实CurveParams也就是 Curve 的实现】
/**
曲线的实现结构体
代码引用路径:crypto/elliptic
代码所在文件路径:src/crypto/elliptic/elliptic.go
*/
type CurveParams struct {
//有限域GF(p)中质数p
P *big.Int
//G点的阶
//如果存在最小正整数n,使得nG=O∞,则n为G点的阶
N *big.Int
//椭圆曲线方程y²= x³-3x+b中常数b
B *big.Int
//G点(x,y)
Gx, Gy *big.Int
//密钥长度
BitSize int
//椭圆曲线名称
Name string
}
func (curve *CurveParams) Params() *CurveParams {
//获取椭圆曲线参数,即curve
return curve
}
func (curve *CurveParams) IsOnCurve(x, y *big.Int) bool {
//是否在曲线y²=x³-3x+b上
// y² = x³ - 3x + b
y2 := new(big.Int).Mul(y, y)
y2.Mod(y2, curve.P)
x3 := new(big.Int).Mul(x, x)
x3.Mul(x3, x)
threeX := new(big.Int).Lsh(x, 1)
threeX.Add(threeX, x)
x3.Sub(x3, threeX)
x3.Add(x3, curve.B)
x3.Mod(x3, curve.P)
return x3.Cmp(y2) == 0
}
func (curve *CurveParams) Add(x1, y1, x2, y2 *big.Int) (*big.Int, *big.Int) {
//加法运算,代码略
}
func (curve *CurveParams) Double(x1, y1 *big.Int) (*big.Int, *big.Int) {
//二倍运算,代码略
}
func (curve *CurveParams) ScalarMult(Bx, By *big.Int, k []byte) (*big.Int, *big.Int) {
//k*(Bx,By),代码略
}
func (curve *CurveParams) ScalarBaseMult(k []byte) (*big.Int, *big.Int) {
//k*G, G为基点,代码略
}
我们再往下看看公私钥对,及签名验签等操作的代码:
//代码位置src/crypto/ecdsa/ecdsa.go
// 公钥
type PublicKey struct {
// 曲线实例
elliptic.Curve
// 公钥对应去上线的一点坐标 (即:kG的坐标,其中名k为私钥,G为基点)
X, Y *big.Int
}
// 私钥
type PrivateKey struct {
// 公钥实例
PublicKey
// 私钥的数字,即kG中的k
D *big.Int
}
// 签名
// rand 随机写入流
// priv 私钥
// 待签名Hash
// @return r 签名的 {r, s}中的r
// @return s 签名的 {r, s}中的s
// @return err
func Sign(rand io.Reader, priv *PrivateKey, hash []byte) (r, s *big.Int, err error) {
entropylen := (priv.Curve.Params().BitSize + 7) / 16
if entropylen > 32 {
entropylen = 32
}
entropy := make([]byte, entropylen)
_, err = io.ReadFull(rand, entropy)
if err != nil {
return
}
md := sha512.New()
md.Write(priv.D.Bytes()) //私钥
md.Write(entropy)
md.Write(hash)
key := md.Sum(nil)[:32]
block, err := aes.NewCipher(key)
if err != nil {
return nil, nil, err
}
csprng := cipher.StreamReader{
R: zeroReader,
S: cipher.NewCTR(block, []byte(aesIV)),
}
c := priv.PublicKey.Curve //椭圆曲线
N := c.Params().N //G点的阶
if N.Sign() == 0 {
return nil, nil, errZeroParam
}
var k, kInv *big.Int
for {
for {
//取随机数k
k, err = randFieldElement(c, csprng)
if err != nil {
r = nil
return
}
//求k在有限域GF(P)的逆,即1/k
if in, ok := priv.Curve.(invertible); ok {
kInv = in.Inverse(k)
} else {
kInv = fermatInverse(k, N) // N != 0
}
//求r = kG
r, _ = priv.Curve.ScalarBaseMult(k.Bytes())
r.Mod(r, N)
if r.Sign() != 0 {
break
}
}
e := hashToInt(hash, c) //e即哈希
s = new(big.Int).Mul(priv.D, r) //Dr,即DkG
s.Add(s, e) //e+DkG
s.Mul(s, kInv) //(e+DkG)/k
s.Mod(s, N) // N != 0
if s.Sign() != 0 {
break
}
//签名为{r, s},即{kG, (e+DkG)/k}
}
return
}
// 验签
// pub 公钥
// hash 等待和签名做对比的被签名的原文Hash (和 签名方法入参中的待签名Hash)
// r 签名的 {r, s}中的r
// s 签名的 {r, s}中的s
// @return bool 是否通过校验 true 是 false 否
func Verify(pub *PublicKey, hash []byte, r, s *big.Int) bool {
c := pub.Curve //椭圆曲线
N := c.Params().N //G点的阶
if r.Sign() <= 0 || s.Sign() <= 0 {
return false
}
if r.Cmp(N) >= 0 || s.Cmp(N) >= 0 {
return false
}
e := hashToInt(hash, c) //e即哈希
var w *big.Int
//求s在有限域GF(P)的逆,即1/s
if in, ok := c.(invertible); ok {
w = in.Inverse(s)
} else {
w = new(big.Int).ModInverse(s, N)
}
u1 := e.Mul(e, w) //即e/s
u1.Mod(u1, N)
u2 := w.Mul(r, w) //即r/s
u2.Mod(u2, N)
var x, y *big.Int
if opt, ok := c.(combinedMult); ok {
x, y = opt.CombinedMult(pub.X, pub.Y, u1.Bytes(), u2.Bytes())
} else {
x1, y1 := c.ScalarBaseMult(u1.Bytes()) //即eG/s
x2, y2 := c.ScalarMult(pub.X, pub.Y, u2.Bytes()) //即DGr/s
//即eG/s + DGr/s = (e + Dr)G/s
//= (e + Dr)kG / (e + DkG) = (e + Dr)r / (e + Dr) = r
x, y = c.Add(x1, y1, x2, y2)
}
if x.Sign() == 0 && y.Sign() == 0 {
return false
}
x.Mod(x, N)
return x.Cmp(r) == 0
}使用如下:
package main
import (
"crypto/ecdsa"
"crypto/elliptic"
"crypto/rand"
"log"
"fmt"
"crypto/sha256"
)
func main() {
// 先获取一个椭圆实例
curve := elliptic.P256()
//得到私钥
privateKey, err := ecdsa.GenerateKey(curve, rand.Reader)
if err != nil {
log.Panic(err)
}
//产生公钥
publicKey := privateKey.PublicKey
fmt.Println("priKey", privateKey, "\npubKey", publicKey)
strHash := sha256.New().Sum([]byte( "我是学生"))
// 签名
r, s, err := ecdsa.Sign(rand.Reader, privateKey, strHash)
if nil != err {
log.Panic(err)
}
fmt.Println("r", r, "\ns", s)
strHash2 := sha256.New().Sum([]byte("我是个程序员"))
// 验签
fmt.Println(ecdsa.Verify(&publicKey, strHash2, r, s)) // false
fmt.Println(ecdsa.Verify(&publicKey, strHash, r, s)) // true
}
好了,以上就是对椭圆曲线加密的讲解,其实以太坊中不是直接用go的原生库crypto中的ecdsa哦,而是用了比特币所使用的一个C++的库 libsecp256k1,在目录:crypto/secp256k1 路径中。
【本文还未写完,国庆这几天会完善完.......】