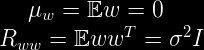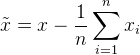Whiten process——数据的白化处理
1.什么是白化处理
“白化”这个词最早来源于信号处理领域，跟其中最常见的一种噪声——白噪声有很大的联系[1]。在信号处理理论中，白噪声指的是一种在不同频率都有相同功率的随机信号，即其功率谱密度为常数，功率与频率无关。“白噪声”这个名字来源于白光，白光包含了光谱中所有的颜色,其功率谱密度也呈平坦状，类似地，“白噪声”这种噪声中包含了所有频率的噪声，因此被冠上了“白”的称号[2]。其他不满足该功率谱密度特性的噪声也被称为有色噪声，类似于非白光的其他颜色光。
上述关于白色信号（白光，白噪声）的定义是一个通俗的定义，其严格数学定义为：一个随机向量w称为一个白色随机向量当且仅当其平均值函数为0且自相关函数为一个单位矩阵的倍数。简单来讲，就是该信号的平均值为0，且各个分量之间互不相关。
明白了白色的定义之后，“白化”的概念也就很容易理解了，也就是把一个不满足上述特性的信号变成具有上述特性的信号，同时能够保留原信号的某些特征。
2.如何进行白化
2.1 零均值化
使得一组数据均值为零的方法很简单：求出当前数据的平均值，然后用原数据减去均值得到的新的数据就是一组均值为零的数据，因为这个过程只是使得数据在数值上共同向上或者向下平移，并不会改变数据的其他特征。而在数据挖掘的过程中，其绝对数值可能很大，如果直接对数据进行分析，那么数据间的差异与其绝对数值相比可能会很小，这样的微小差异所蕴含的信息就不容易被挖掘到，因此在数据处理前进行零均值化处理是一种很常见的预处理手段。
具体来讲，设原始数据为x，其维数为n，那么零均值化之后的数据
可以由如下式子得到
2.2白化变换
接下来考虑白化的第二个条件，我们需要使得白化后的数据各个维度之间不相关，具体来讲，我们通过白化变换完成这个过程。白化变换[3]是一种可以将已知协方差矩阵的随机向量变成一系列新的变量组成的向量使得新的向量协方差矩阵为一个单位矩阵。这对应着白化定义中方差
=1的情况，表示了一种白化的标准型。为什么在白化变换中一定要求白化后的方差为1呢？举个例子，在信号处理中，一个随机信号u通过一个放大率为100的线性放大器得到另一个随机变量w，从方差的角度看其方差变为原来的10000倍，看起来是另一个与u完全不同的信号，但是实际上只是数值按比例放大，比如采用了不同的计量单位来量化同一个物理信号，两个看似不同的信号却描述了同一个物理现象。为了避免这种情况，最好在白化变换中将信号的整体方差也归一化为1，这样就可以避免类似的问题。
一些容易与白化变换混淆的概念包括：去相关化、标准化、有色变换。去相关化仅仅使得各个分量之间不相关，而对于整体的方差没有进行考虑。标准化使得整体的方差为1但是没有考虑相关性。有色变换是使得一个白色随机序列根据设计好的相关性矩阵变成一个要求的有色序列。
白化变换的数学定义如下：假设
是一个均值为0的随机向量，其协方差矩阵为
且非奇异。一个线性变换
称为白化变换当且仅当
因为这样得到的新的向量Y的协方差矩阵就为单位矩阵。
白化变换的关键就是求出满足上述条件的变换矩阵W，求解方法不唯一，包括ZCA白化（
), Cholesky白化（Cholesky 分解）和PCA白化（PCA分解）。
3为何要进行白化
在机器学习的过程中，输入数据常常为各种测量量，相邻采样点之间的数据具有很强的相关性。比如一幅图像中，非边缘部分的相邻像素与中心像素之间差异一般很小，如果全部输入网络中进行训练，就会有很大的数据冗余，使得整个网络的训练效率不高。如果对输入数据进行白化处理，就能降低数据之间的相关度，不同数据所蕴含的信息之间的重复性就会降低，网络的训练效率就会提高。
参考资料：
[1] https://en.wikipedia.org/wiki/Whitening_transformation
[2] https://en.wikipedia.org/wiki/White_noise
[3] https://en.wikipedia.org/wiki/Whitening_transformation