NLP笔记 CS224n(1)—— 词向量
词向量
NLP 处理文本,所以在进行处理之前,要先解决文本的表示。文本由词组成,本文讨论了表示词汇的几种方案。
WordNet
这种方法基于如下思想:用词汇的意义来代表词。所以我们可以建立若干个集合,每个集合代表一组同义词,每个词都可以映射到某个集合中,表示这个词汇的意思。
其优点在于可以很好的处理词汇之间的联系,即同义词。但是缺点同样明显:
- 忽略了同义词之间的差异,忽略了一词多义性
- 难以迭代更新,忽略词语的新含义
- 基于主观判断
- 需要专家进行手动构造
- 不能准确计算词汇间的相关性
Discrete Symbols (one-hot code)
这种方法即对词汇进行独热编码,用一个数字来表示一个词,但是这种方法中,任何两个词的编码都是完全独立的,也就是说这种方法无法表征词汇之间的相关性。自然语言中一个词汇和其他词汇的关系对词语意义的解释有着很大的影响,所以这种方法的局限性也很大。
Word Vector
我们希望得到一种既简单又能够很好的表示词汇间关系的编码方式。所以我们可以将先前两种方案的思想结合起来,得到词向量的编码方式。这种方法基于如下假设:一个词汇的含义可以由经常在其边上出现的词汇决定。
思想
基于这种编码方式,我们有Word2Vec框架的核心思想如下:
- 有一个巨大的语料库
- 每个词语都被一个定长的向量表示
- 对语料库中每个词,称其为中心词(center) c c c,其周围定长距离内的词称为上下文(outside) o o o
- 使用词向量来表示 P ( o ∣ c ) P(o|c) P(o∣c)
- 迭代每个词对应的向量来优化系统
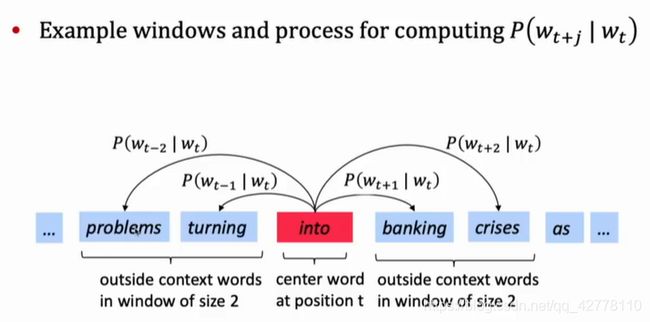
如图所示,我们可以做出如下陈述,into的词义由problems,turning,banking,crises等其附近的词给出。类似地,随着中心词后移,可以产生多组这种关系。
定义式
接下来给出这种概念的定量描述:
定义整个词汇空间为 V V V 表示所有词汇的集合,其中第 i i i 个词为 v i v_i vi ;向量空间为 θ \theta θ 表示所有词汇对应的词向量构成的集合。定义 T T T 为语料库,其中第 i i i 个词为 w i w_i wi 。 我们定义相似度 L ( θ , T ) L(\theta,T) L(θ,T) 为词向量集 θ \theta θ 在语料库 T T T 上的拟合程度。我们可以认为 T T T 是一个常量,所以只考虑参数 θ \theta θ ,相似度有计算式如下:
L ( θ ) = Π t = 1 ∣ T ∣ Π − m ≤ j ≤ m , j ≠ 0 P ( w t + j ∣ w t , θ ) L(\theta) = \Pi_{t=1}^{|T|}\Pi_{-m\leq j\leq m,j\not=0}P(w_{t+j}|w_{t},\theta) L(θ)=Πt=1∣T∣Π−m≤j≤m,j=0P(wt+j∣wt,θ)
为了标准化,可以加入平均值;而log几乎对所有连乘的目标函数都实用,所以可以得到目标函数:
J ( θ ) = − 1 ∣ T ∣ log ( L θ ) J(\theta) = -\frac{1}{|T|}\log(L_\theta) J(θ)=−∣T∣1log(Lθ)
我们希望最大化词向量集对这个语料库的拟合程度,所以可以得到优化目标:
θ = arg max θ J ( θ ) \theta = \arg\max_\theta J(\theta) θ=argθmaxJ(θ)
如此便可得到词向量的计算方式。
从语料库到词向量
事实上,我们可以这样解释这个过程,我们考虑词汇空间为一个离散点集,从每个点出发向其他点连一条有向边,对于点 c c c 指向点 o o o 的边,我们记为 c → o c\rightarrow o c→o,有边权 W ( c → o ) = P ( o ∣ c ) W(c\rightarrow o)=P(o|c) W(c→o)=P(o∣c)。这个概率表示从某个点转移到其他点的概率分布,且满足 ∑ i = 1 ∣ V ∣ P ( v i ∣ u ) = 1 \sum_{i=1}^{|V|}P(v_i|u)=1 ∑i=1∣V∣P(vi∣u)=1,类似一个马尔可夫过程。 在上面的计算式中,我们不停累计 P ( w t + j ∣ w t ) P(w_{t+j}|w_{t}) P(wt+j∣wt),也就是计算出每条边出现的次数。现在我们要设置边权,来使得上式最大化,事实上是希望拟合这样一个分布,使得出现次数多的尽量大,在这个情形下,只要将其出现次数最多的后继边权置为1即可,这样可以得到类似于 WordNet 的一种分类结果。
到目前为止,似乎都没有词向量什么事,因为只要设置边权即可。但是需要注意的是,事实上这些边权按照顺序排序即可得到一个长度等长于向量空间的词向量,且天然具有归一化的性质。
特别地说,如果我们对相似性的要求更加严格一些,比如规定为其后特定位置出现的同样的词语,那么我们可以在这个基础上构建更多的边,如下一个词边,下两个词边,上一个词边等等,对应的词向量也会加长。如果要将一些边合并,可以将其加权合到同一条边中。诸如此类。更一般地说,我们可以通过修改对图上边的定义来取得对相似性不同的定义。
这种方法可以在某种程度上刻画词语的相似性,比如 h e he he 之后经常出现 h a s has has , s h e she she 之后也经常出现 h a s has has ,则在与 h a s has has 相连的这个向量上,他们的值可能都是1,从而将相似性存储在编码中。但是在上述情形下,这种分类过于严格,则出现次数次高的词或者几种相仿的结果可能被丢掉。
而且但是这样的话,存储这些词向量将需要 O ( n 2 ) O(n^2) O(n2) 的空间, n n n 经常能达到百万数量级甚至更大,因此,考虑将信息压缩,也就是说,我们给每个词一个向量,从而隐式的存储 W ( c → o ) = P ( o ∣ c ) W(c\rightarrow o)=P(o|c) W(c→o)=P(o∣c) 的值。假设给每个词分配长度为 ∣ V ∣ |V| ∣V∣ 的向量,则其中一个全局最优解即上面所述的概率模型。但事实上可以分配远小的多的长度,如100,则复杂度降低为 O ( 200 n ) O(200n) O(200n),因为一个词作为中心词和边缘词不同,一种解决方案是将其拆开,用 v v v 表示中心词, u u u 表示上下文。可以用下式来代替 P ( o ∣ c ) P(o|c) P(o∣c):
P ( o ∣ c , θ ) = e x p ( u o T ⋅ v c ) ∑ w ∈ V e x p ( u w T ⋅ v c ) P(o|c,\theta)=\frac{exp(u_o^T\cdot v_c)}{\sum_{w\in V}exp(u_{w}^T\cdot v_c)} P(o∣c,θ)=∑w∈Vexp(uwT⋅vc)exp(uoT⋅vc)
即一个softmax函数,其有如下优势:
结果
可以梯度下降法等优化方法求解,对于某个o,可以使用链式法则暴力展开求偏导如下:
∂ ∂ v c = u o − ∑ x ∈ V P ( x ∣ c ) u x \frac{\partial}{\partial v_c} = u_o-\sum_{x\in V}P(x|c)u_x ∂vc∂=uo−x∈V∑P(x∣c)ux
这个偏导恰好表示表示o本身的向量,和从c转移一次后的期望向量之差。做梯度下降实质上在降低这个差。
而对于J的偏导数,因为结果上由log,所以直接对所有的o的 ∂ ∂ v c \frac{\partial}{\partial v_c} ∂vc∂ 求和即可。
