【CS224n】笔记8 RNN和语言模型
1 语言模型
语言模型就是计算一个单词序列(句子)的概率(P(w1,…,wm))的模型。

或者在机器翻译的问题中:
在翻译"猫很小"时,单词的语序问题中我们会使概率 P(the cat is small) > P(small the is cat);
在翻译"放学后走回家"时,单词的选择问题中我们会使概率 P(walking home after school) > P(walking house after school)
2 传统语言模型
当前我们很难为所有的语序计算概率,所以我们只关注窗口下的前n个单词来预测当前词的概率。当然这是不正确但是必须的马尔科夫假设:

n-gram模型:

为了估计此条件概率,常用极大似然估计,比如对于BiGram(2元语言模型)和TriGram(3元语言模型)模型,有:
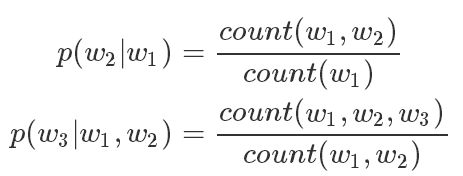
如果选择2元语言模型,语义2元组的词频通过统计当前词和其前面一个词,这就需要与1元语法模型的词频计算方法区分开来。上面两个公式分别展示了2元语义模型和3元语言模型在处理这种关系时的做法,都是通过语料中的先验也就是通过计数的方式来计算。
计算示例:
传统的语言模型存在的问题:
其中count()为一个计数函数,它是负责计算对应词序在语料中出现的频数。由上面几部分显然,当n越大,马尔科夫假设效果就越弱,计算出来的概率值也就越接近于真实值,当然n越大,我们的计算量也就越大(鱼和熊掌不可兼得)。
这些ngram可能会占用上G的内存,在最新的研究中,一个1260亿的语料在140G内存的单机上花了2.8天才得到结果。
3 递归神经网络RNN
解决传统语言模型问题的办法: 递归神经网络(Recurrent Neural Networks)
语言模型其实就是时间序列模型,我们从左到右的说活,一句正确的话中词与词之间是有顺序和时间的,比如t0时刻先说“我”,t1时刻再说“爱”,最后的t2时刻再说“你”。
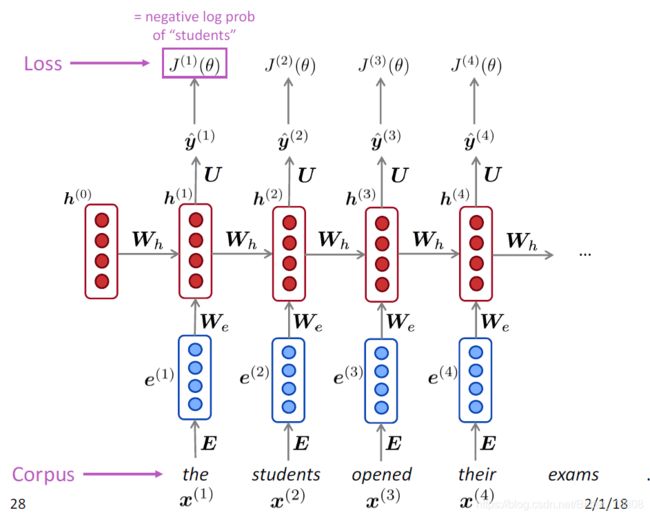
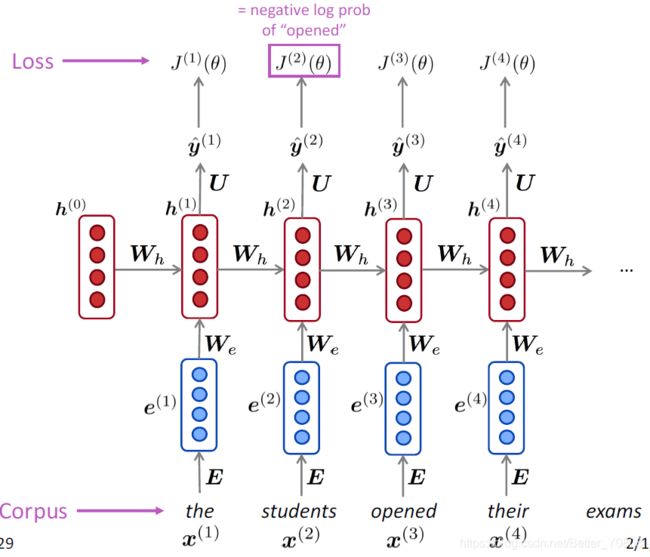
新的语言模型是利用RNN对序列建模,复用不同时刻的线性非线性单元及权值,理论上之前所有的单词都会影响到预测单词。
不同于传统的机器翻译模型仅仅考虑有限的前缀词汇信息作为语义模型的条件项,递归神经网络(RNN)有能力将语料集中的全部前序词汇纳入模型的考虑范围。
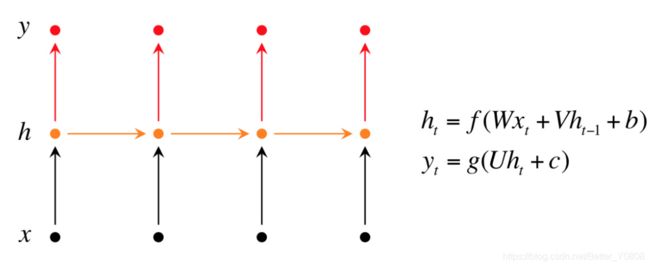
给定一个词向量序列: x 1 x_1 x1…, x t − 1 x_{t-1} xt−1, x t x_t xt, x t + 1 x_{t+1} xt+1… x T x_T xT,在每个时间点上都有隐藏层的特征表示:
![]()

在第一个或者0步长时,将 h 0 h_0 h0进行随机初始化,因为0步长时,还没有产生 h 0 h_0 h0。
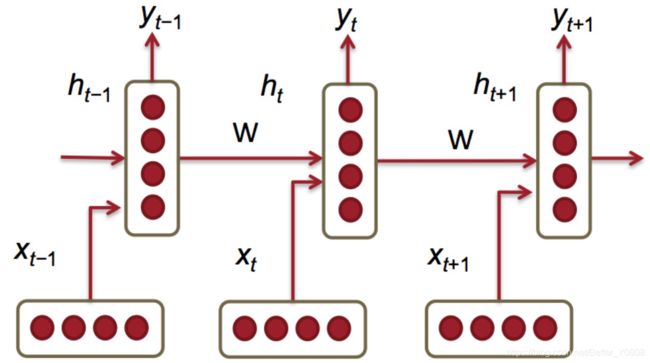
一个RNN的模型如下图(感觉这个之前的PPT比224n的易懂一些)
上图是展开的RNN,未展开的的RNN如下两个图所示:
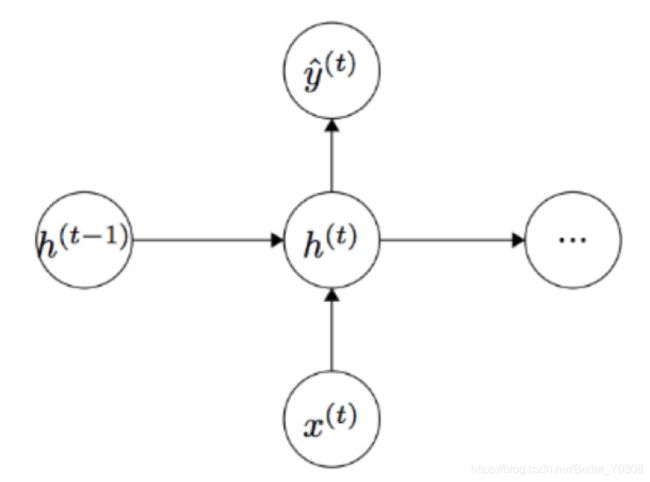
等效于:
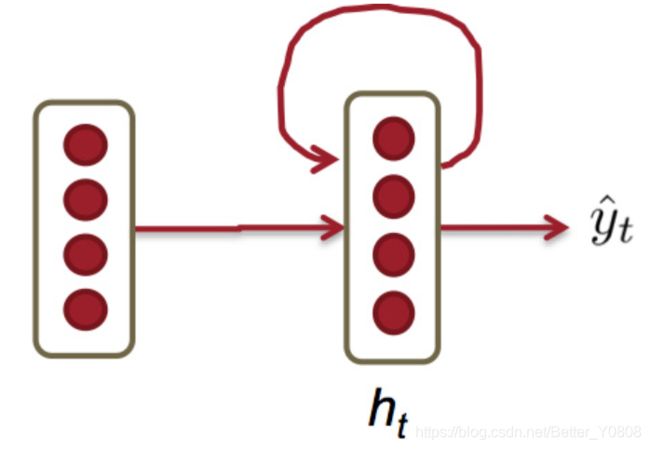
一般情况下我们以展开形式来理解RNN,但是实际上他们就是一个相同单元的展开,可以理解为每个单元的参数是共享的。
我们现在的任务不是分类而是预测下一个单词出现的概率值,所以我们需要拟合的就是:
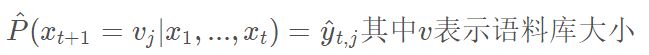
所需内存只与语料库大小成正比,不取决于序列长度。
因此在t时刻损失函数也采用交叉熵loss function,但是此时已经不是预测类别,而是预测单词:
(预测下一个单词应该是语料库中的哪一个单词,在t时刻,语料库中哪个单词的概率最大)

由上式我们显然可得到,整个序列的损失函数为:

直观图如下:在每一个时间点t,都有一个loss
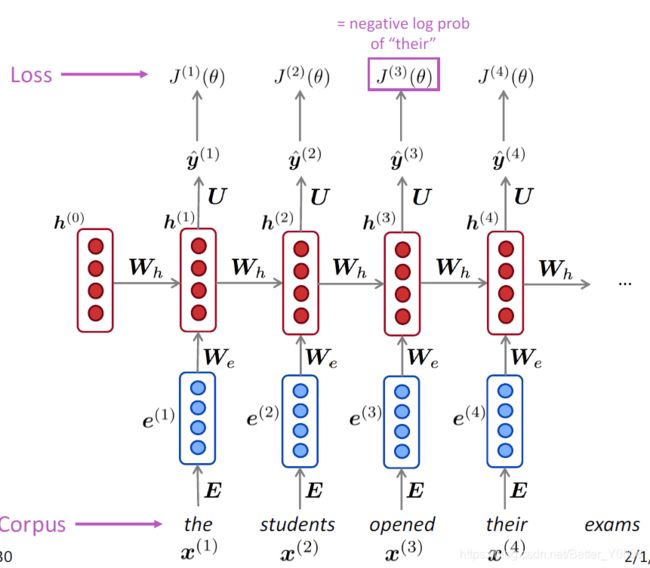
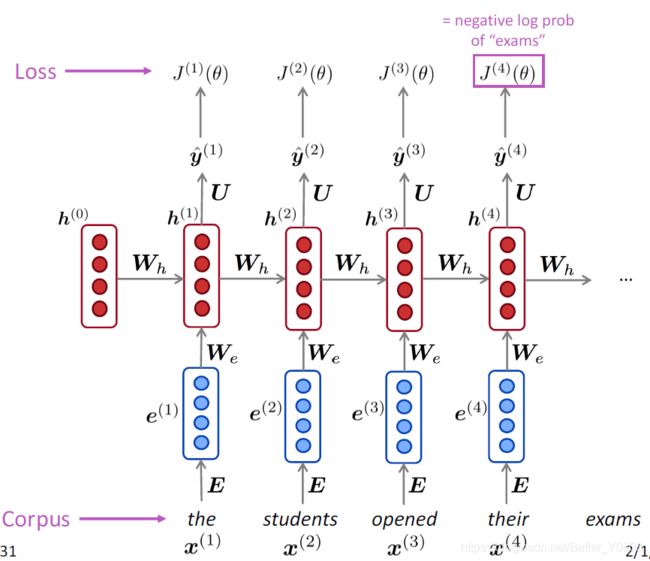

如果以22为底数会得到“perplexity困惑度”,代表模型下结论时的困惑程度,越小越好:

3. 训练神经网络面临的问题和技巧
观察句子1:
“Jane walked into the room. John walked in too. Jane said hi to ___”
以及句子2:
“Jane walked into the room. John walked in too. It was late in the day, and everyone was walking home after a long day at work. Jane said hi to ___”
人类可以轻松地在两个空中填入“John”这个答案,但RNN却很难做对第二个。这是因为在前向传播的时候,前面的x反复乘上W,导致对后面的影响很小。
此外,RNN和普通的神经网络的训练过程有些许不同,对于普通的神经网络,我们一般是自上而下的进行梯度计算,但是RNN特殊之处就在于,他的梯度有自上而下,自右向左两个方向来源,如下图:
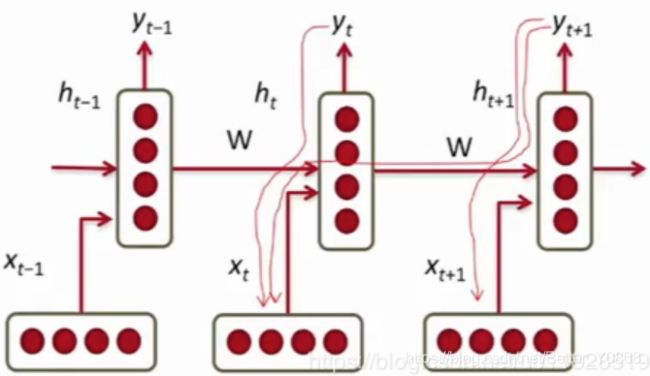
梯度消失/爆炸出现的原因
梯度消失是什么?为什么会出现梯度消失?下面我们来看一下RNN的反向传播过程。
假设我们的RNN公式形式和上面定义保持一致:
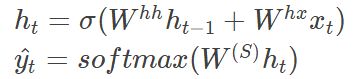
对于RNN结构来说,由于我们在序列的每个位置都有损失,所以最终的损失函数为:
![]()
其中 W ( S ) W^{(S)} W(S)的梯度计算是比较简单的:
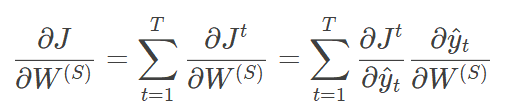
但是 W h h W^{hh} Whh和 W h x W^{hx} Whx的梯度计算就比较的复杂了。从RNN的模型可以看出,在反向传播时,在t时刻的梯度损失由当前位置的输出对应的梯度损失(从上到下)和t+1时的梯度损失(从右到左)两部分共同决定。对于W在某一时刻t的梯度损失需要反向传播一步步的计算。为了方便后面的重复利用,我们定义时刻t的隐藏状态的梯度为 δ ( t ) δ^{(t)} δ(t) :

由此我们可以跟普通的神经网络一样,由 δ ( t + 1 ) δ^{(t+1)} δ(t+1)推导出 δ ( t ) δ^{(t)} δ(t):

显然上式中第一部分为从上到下传播的梯度;第二部分为从右往左传播的梯度。
为了方便运算书写,我们假设 h t h_t ht的激活函数σ()变为tanh()函数(PS:激活函数的一种,不影响求导思路,此处替换仅仅是为了方便运算),因此 W ( h h ) W^{(hh)} W(hh) 和 W ( h x ) W^{(hx)} W(hx) 的求偏导过程如下:
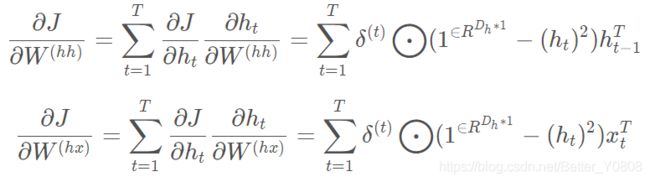

其实以上过程也跟第四讲中的推倒过程类似,我是先通过求 W h h W^{hh} Whh矩阵中单一元素的偏导数,然后拓展到矩阵求导,下面是对 W i j h h W^{hh}_{ij} Wijhh的求导过程, W i j h x W^{hx}_{ij} Wijhx类似,所以此处只推导 W i j h h W^{hh}_{ij} Wijhh:

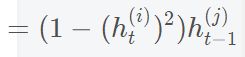
由上式单个变量的偏导数我们就可以推导出他们的矩阵形式,以上推导过程如有错误,请不吝赐教。
从上面的推导过程中我们可以看到在对W求导的时候:
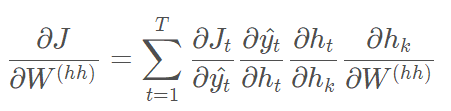
其中上式中:
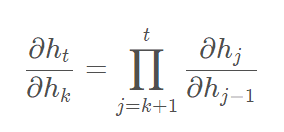
上式中每一个偏导数都是一个雅可比Jacobain行列式:

对于雅可比行列式,我们可以假设他的范数的上限为β,则我们可以得到:
(已知一个矩阵,就能得到矩阵的范数)
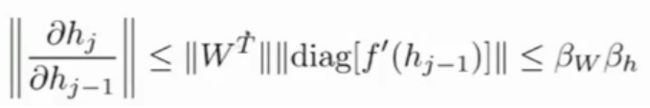
则W的梯度是一系列雅可比行列式范数的乘积:
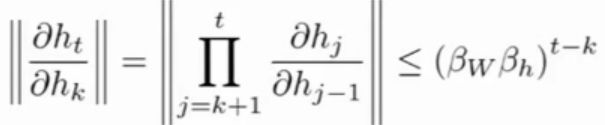
由上式我们可知,当我们初始化时,行列式的范数大于1时,梯度就会出现变得无限大,这就是梯度爆炸;行列式范数小于1时,梯度就会变得无限小,这就是梯度消失。对于普通的神经网络梯度消失会造成神经网络前几层的参数变化很小或者几乎不更新。
- 梯度消失出现的实例
import numpy as np
import matplotlib.pyplot as plt
#sigmoid函数
def sigmoid(x):
x=1/(1+np.exp(-x))
return x
#sigmoid导函数
def sigmoid_grad(x):
return x*(1-x)
#Relu激活函数
def relu(x):
return np.maximum(0,x)
def three_layer_net(NONLINEARITY,X,y,model,step_size,reg):
#参数初始化
h=model['h']
h2=model['h2']
W1=model['W1']
W2 = model['W2']
W3 = model['W3']
b1=model['b1']
b2 = model['b2']
b3 = model['b3']
num_examples=X.shape[0]
plot_array_1=[]
plot_array_2=[]
for i in range(50000):
#前向传播
if NONLINEARITY=='RELU':
hidden_layer=relu(np.dot(X,W1)+b1)
hidden_layer2=relu(np.dot(hidden_layer,W2)+b2)
scores=np.dot(hidden_layer2,W3)+b3
elif NONLINEARITY == 'SIGM':
hidden_layer = sigmoid(np.dot(X, W1) + b1)
hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
exp_scores=np.exp(scores)
probs=exp_scores/np.sum(exp_scores,axis=1,keepdims=True)#softmax概率化得分[N*K]
#计算损失
correct_logprobs=-np.log(probs[range(num_examples),y])#整体的交叉熵损失
data_loss=np.sum(correct_logprobs)/num_examples #平均交叉熵损失
reg_loss=0.5*reg*np.sum(W1*W1)+0.5*reg*np.sum(W2*W2)+0.5*reg*np.sum(W3*W3)#正则化损失,W1*W1表示哈达玛积
loss=data_loss+reg_loss
if i%1000==0:
print("iteration %d: loss %f"%(i,loss))
#计算scores的梯度
dscores=probs
dscores[range(num_examples),y]-=1 #此处为交叉熵损失函数的求导结果,详细过程请看:https://blog.csdn.net/qian99/article/details/78046329
dscores/=num_examples
#反向传播过程
dW3=(hidden_layer2.T).dot(dscores)
db3=np.sum(dscores,axis=0,keepdims=True)
if NONLINEARITY == 'RELU':
# 采用RELU激活函数的反向传播过程
dhidden2 = np.dot(dscores, W3.T)
dhidden2[hidden_layer2 <= 0] = 0
dW2 = np.dot(hidden_layer.T, dhidden2)
plot_array_2.append(np.sum(np.abs(dW2)) / np.sum(np.abs(dW2.shape)))
db2 = np.sum(dhidden2, axis=0)
dhidden = np.dot(dhidden2, W2.T)
dhidden[hidden_layer <= 0] = 0
elif NONLINEARITY == 'SIGM':
# 采用SIGM激活函数的反向传播过程
dhidden2 = dscores.dot(W3.T) * sigmoid_grad(hidden_layer2)
dW2 = (hidden_layer.T).dot(dhidden2)
plot_array_2.append(np.sum(np.abs(dW2)) / np.sum(np.abs(dW2.shape)))
db2 = np.sum(dhidden2, axis=0)
dhidden = dhidden2.dot(W2.T) * sigmoid_grad(hidden_layer)
dW1 = np.dot(X.T, dhidden)
plot_array_1.append(np.sum(np.abs(dW1)) / np.sum(np.abs(dW1.shape)))#第一层的平均梯度记录下来
db1 = np.sum(dhidden, axis=0)
# 加入正则化得到的梯度
dW3 += reg * W3
dW2 += reg * W2
dW1 += reg * W1
# 记录梯度
grads = {}
grads['W1'] = dW1
grads['W2'] = dW2
grads['W3'] = dW3
grads['b1'] = db1
grads['b2'] = db2
grads['b3'] = db3
# 更新梯度
W1 += -step_size * dW1
b1 += -step_size * db1
W2 += -step_size * dW2
b2 += -step_size * db2
W3 += -step_size * dW3
b3 += -step_size * db3
# 评估模型的准确度
if NONLINEARITY == 'RELU':
hidden_layer = relu(np.dot(X, W1) + b1)
hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2)
elif NONLINEARITY == 'SIGM':
hidden_layer = sigmoid(np.dot(X, W1) + b1)
hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))
# 返回梯度和参数
return plot_array_1, plot_array_2, W1, W2, W3, b1, b2, b3
if __name__=='__main__':
plt.rcParams['figure.figsize']=(10.0,8.0)#设置画布的默认大小
plt.rcParams['image.interpolation']='nearest'#设置插值的风格
plt.rcParams['image.cmap']='gray'#设置画布的颜色
np.random.seed(0)#保证后面seed(0)生成的随机数相同
N=100 #每一个类别的数量
D=2 #维度
K=3 #类别数
h=50
h2=50
X=np.zeros((N*K,D))
num_train_examples=X.shape[0]
y=np.zeros(N*K,dtype='uint8')
for j in range(K):
ix=range(N*j,N*(j+1))
r=np.linspace(0.0,1,N) # 半径
t=np.linspace(j*4,(j+1)*4,N)+np.random.randn(N)*0.2 # theta
X[ix]=np.c_[r*np.sin(t),r*np.cos(t)]# 按行拼接两个矩阵
y[ix]=j
fig=plt.figure()
plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral)#画点,c代表颜色,s代表点的大小
plt.xlim([-1,1])#设置横坐标的范围大小
plt.ylim([-1,1])#设置纵坐标的范围大小
plt.show()
#初始化模型参数
h = 50
h2 = 50
model={}
model['h'] = h # hidden layer 1 大小
model['h2']= h2# hidden layer 2 大小
model['W1']= 0.1 * np.random.randn(D,h)
model['b1'] = np.zeros((1,h))
model['W2'] = 0.1 * np.random.randn(h,h2)
model['b2']= np.zeros((1,h2))
model['W3'] = 0.1 * np.random.randn(h2,K)
model['b3'] = np.zeros((1,K))
Activation_Function='RELU'#选择激活函数 SIGM/RELU
(plot_array_1, plot_array_2, W1, W2, W3, b1, b2, b3) = three_layer_net(Activation_Function, X, y, model,step_size=1e-1, reg=1e-3)
#模型采用两种激活函数时,分别画出模型梯度的变化趋势
plt.plot(np.array(plot_array_1))
plt.plot(np.array(plot_array_2))
plt.title('Sum of magnitudes of gradients -- hidden layer neurons')
plt.legend((Activation_Function+" first layer", Activation_Function+" second layer"))
plt.show()
上述程序中先制造训练数据,如下图:
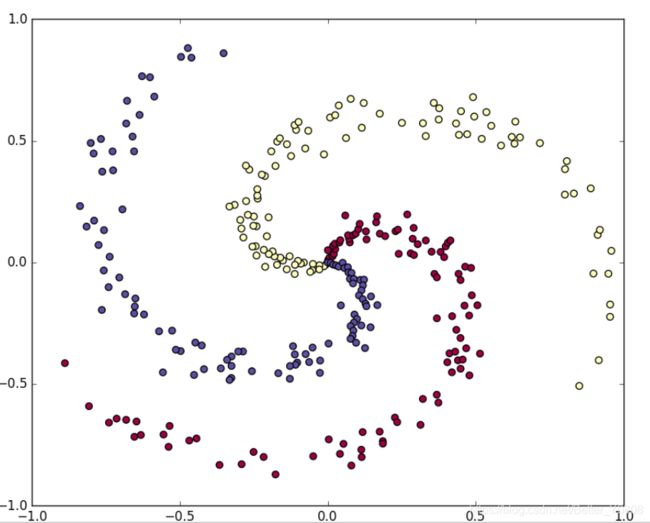
学习非线性的决策边界:
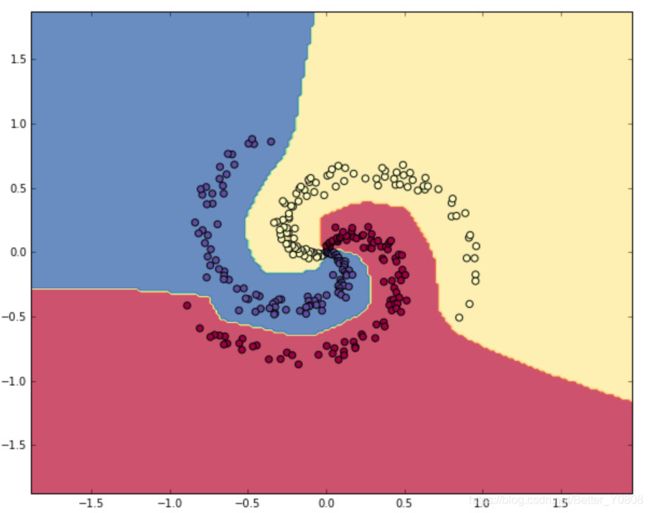
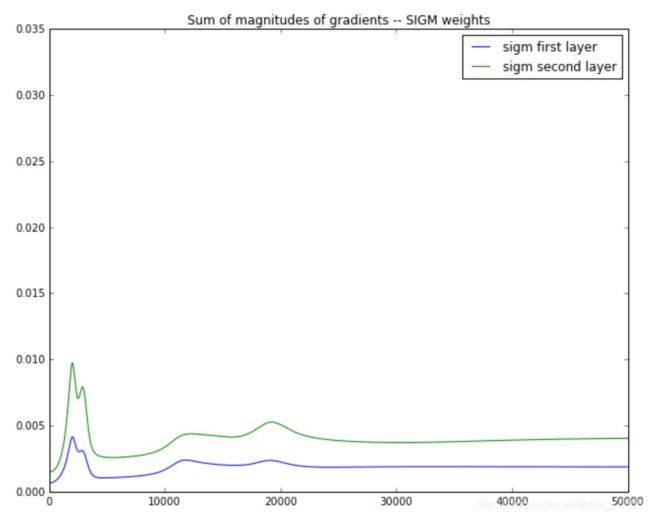
然后分别采用sigmoid和RELU函数当做激活函数来训练模型,并记录模型中各层梯度的变化,效果如下:
sigmoid激活函数下:
ReLU激活函数下:
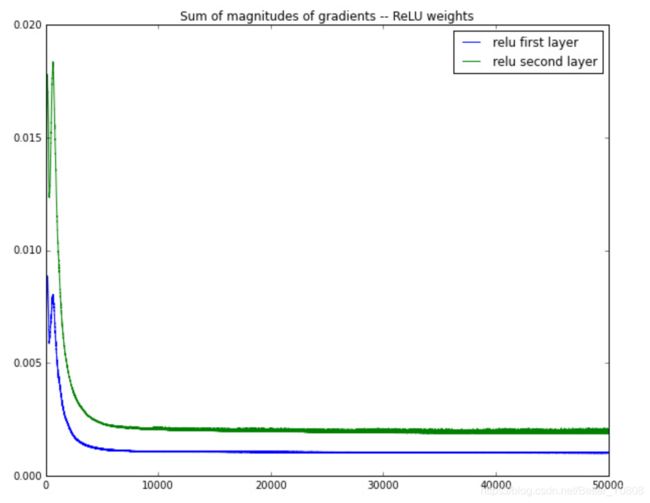
在这个例子的反向传播中,相邻两层梯度是近乎减半地减小。
由上图我们可以看出(PS:上图中的第一层和第二层,是相对于神经网络正向传播时距离起点输入的层数),反向传播的过程中,距离反向传播的起点越远,梯度的变化值越小,如果神经网络的层数很多,最终可能梯度就会消失,导致前面层数的参数不更新,这就是梯度消失现象。
- 处理梯度爆炸技巧
一种暴力的方法是,当梯度的长度大于某个阈值的时候,将其缩放到某个阈值。虽然在数学上非常丑陋,但实践效果挺好。通常采用clip gradient算法,其伪代码如下:

这个方法是Thomas Mikolov首先提出的,大体思想就是设置一个阈值,当梯度大于这个阈值的时候就截断,这个方法听上去很无脑,但是实际效果还不错。
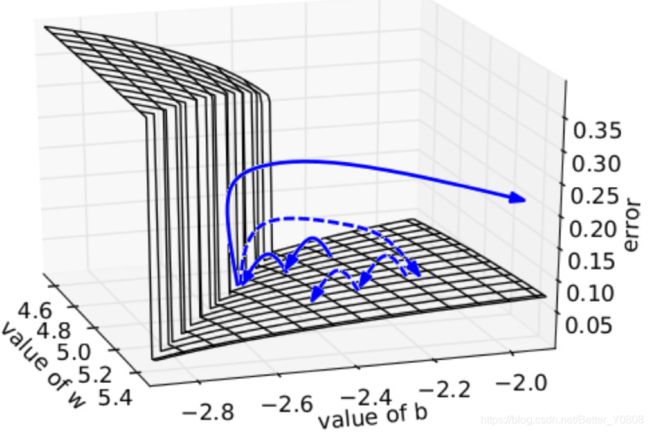
其直观解释是,在一个只有一个隐藏节点的网络中,损失函数和权值w偏置b构成error surface,其中有一堵墙:
每次迭代梯度本来是正常的,一次一小步,但遇到这堵墙之后突然梯度爆炸到非常大,可能指向一个莫名其妙的地方(实线长箭头)。但缩放之后,能够把这种误导控制在可接受的范围内(虚线短箭头)。
但是这种方法没法儿应用到梯度消失,因为当梯度很小的时候,说明某一些维度的特征权重要不变了,如果这时候设置一个最小值的阈值,则会让这些维度的特征权重继续变化,因此得证:clip gradient不能应用到梯度消失。
- 处理梯度消失技巧
处理梯度消失的方法大体就是
(1) 对W不采用随机初始化,初始化为单位矩阵;这样初始效果就是上下文向量和词向量具有相同权重,减少随机性。
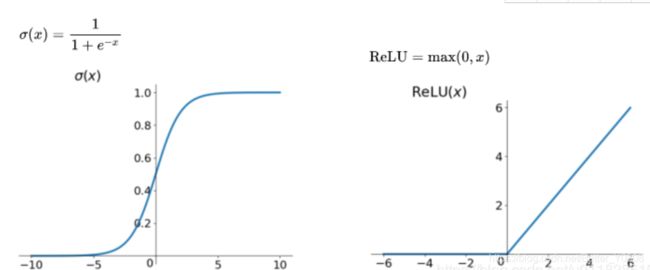
(2)激活函数采用Relu函数,从Relu和Sigmoid函数的图像我们可以知道,sigmoid的梯度在饱和区域非常平缓,接近于0,很容易造成梯度消失的问题;而Relu的梯度大多数情况下是常数。
5 RNN应用于其他序列任务
有了RNN,我们可以用它来做哪些任务呢?课程中讲到,有NER(命名实体识别)、上下文中实体层次情感分析、观点表达分类等 。
文中以RNN进行意见挖掘为例:

其中,意见挖掘任务就是将每个词语归类为:
DSE:直接主观描述(明确表达观点等)
ESE:间接主观描述(间接地表达情感等)
具体的标注方法BIO标注,B表示实体的开始,I表示实体的延续,O表示other。
我们可以用简单的RNN来完成上面任务:
其中x代表输入tokens;y代表标签BIO。
如果过我们考虑到RNN的单向性,而打标签的过程可能依赖上下文,那么我们可以采用双向RNN:

这里箭头表示从左到右或从右到左前向传播,对于每个时刻tt的预测,都需要来自双向的特征向量,拼接后进行分类。箭头虽然不同,但参数还是同一套参数(有些地方是两套参数[1] G. Lample, M. Ballesteros, S. Subramanian, K. Kawakami, and C. Dyer, “Neural Architectures for Named Entity Recognition.,” HLT-NAACL, 2016.)。
当然为了实验效果,也可以加深网络:

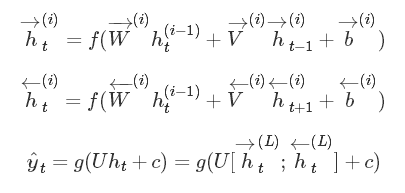
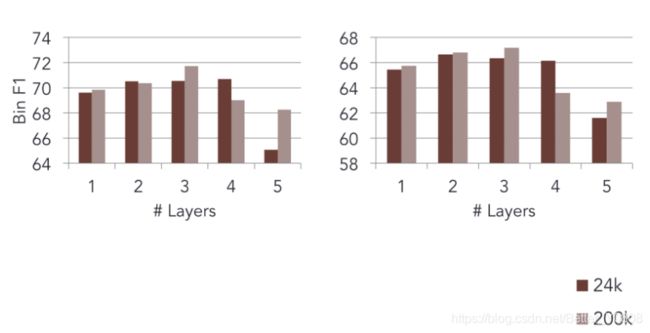
评测方法是标准的F1(因为标签样本不均衡),在不同规模的语料上试验不同层数的影响:
最后的实验结果(F1值)表明,神经网络不是层数越大越好:
参考博客:
https://blog.csdn.net/u011828519/article/details/84782929
http://www.hankcs.com/nlp/cs224n-rnn-and-language-models.html