2020牛客多校 第三场 C-Operation Love （几何 + 顺逆时针判断）

题目链接: C-Operation Love

Description

题意：给出机器人手掌的n个点，判断是左手还是右手

Alice is a beauty in a robot society. So many robots want to marry her. Alice determines to marry a robot who can solve the following puzzle:

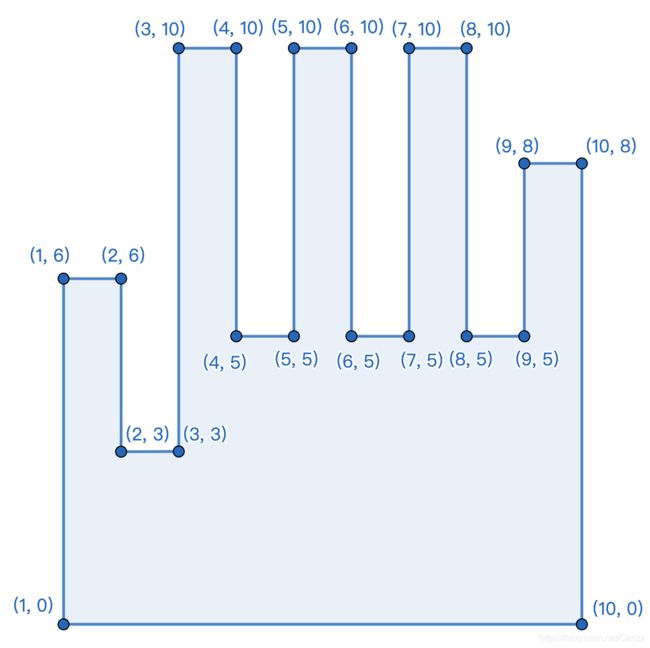
Firstly, the shape of Alice’s right palm is as follow:

And the shape of Alice’s left palm is symmetrical to her right palm.

In this puzzle, Alice will give the challenger many handprints of her palm. The challenger must correctly tell Alice each handprint is her left palm or right palm. Notice that the handprint of Alice’s palm is given by its 2D plane coordinates in clockwise or counterclockwise order. And The shape may be rotated and translated. But the shape won’t be zoomed in nor be zoomed out.

Although you are not a robot, you are interested in solving puzzles. Please try to solve this puzzle.

Input

The first line contains one integer t (1≤t≤10³ ) — the number of handprints in Alice’s puzzle.

Each handprint is described by a simple polygon composed of 20 points. Each point in this polygon will be given in clockwise or counterclockwise order. Each line contains two real numbers with exactly six digits after the decimal point, representing the coordinate of a point. So a handprint is composed of 20 lines in the input.

All values of coordinate in the input is in the range [-1000.0000000, 1000.000000].

Output

For each footprint of palm, print a line contains “right” or “left”, indicating the footprint is the right palm or the left palm respectively.

Sample Input

2
1.000000 0.000000
10.000000 0.000000
10.000000 8.000000
9.000000 8.000000
9.000000 5.000000
8.000000 5.000000
8.000000 10.000000
7.000000 10.000000
7.000000 5.000000
6.000000 5.000000
6.000000 10.000000
5.000000 10.000000
5.000000 5.000000
4.000000 5.000000
4.000000 10.000000
3.000000 10.000000
3.000000 3.000000
2.000000 3.000000
2.000000 6.000000
1.000000 6.000000
-1.000123 0.000000
-10.000123 0.000000
-10.000123 8.000000
-9.000123 8.000000
-9.000123 5.000000
-8.000123 5.000000
-8.000123 10.000000
-7.000123 10.000000
-7.000123 5.000000
-6.000123 5.000000
-6.000123 10.000000
-5.000123 10.000000
-5.000123 5.000000
-4.000123 5.000000
-4.000123 10.000000
-3.000123 10.000000
-3.000123 3.000000
-2.000123 3.000000
-2.000123 6.000000
-1.000123 6.000000

Sample Output

right
left

Method

• 首先对所有顺序给出的点求一次叉乘和，小于0则是逆时针，否则是顺时针；做题的时候并不知道可以用叉乘判断图形的顺逆时针，蒟蒻学到了 555
• 接下来图形就可以已知有规律了，接着找到任意与其他边不同的两条边，我找的是大小为 6 和 9 的边，判断两条边的顺序；
• 右手掌中这两条边的前后顺序与左手掌中的必然不同，将前后顺序和顺逆时针综合判断即可得出是 right 还是 left；补起题来简单，一做就做不出，这就是蒟蒻吗

code

详见注释

#include 
#include 
#include 

using namespace std;
#define Max 1e5+5
#define ll long long
template<typename T> T get(T a, T b, T c, T d) { return a*d-b*c; }					//求叉乘 
template<typename T> T getr(T a, T b, T c, T d) { return (a-b)*(a-b)+(c-d)*(c-d); }	//求两点之间距离 
pair <double, double> pot[20];								//保存所有点 
int T;
bool flag;													//标志顺逆时针 

void print(bool book)										 
{
	if(flag&&book||!flag&&!book) printf("right\n");
	else if(flag&&!book||!flag&&book) printf("left\n");
}

void solve()
{
	double sum = 0;
	for(int i=0; i<20; i++)									//求任意两点的叉乘和 
	{
		int t = (i+1)%20;
		sum += get(pot[i].first, pot[i].second, pot[t].first, pot[t].second);
		//cout << sum << endl;
	}
	flag = sum >= 0 ? true : false;							//如果叉乘和小于0，则说明是逆时针 
	for(int i=0; i<20; i++)									//找到边约为6 9的两条边并进行正反判断 
	{
		double t1 = getr(pot[i].first, pot[(i+1)%20].first, pot[i].second, pot[(i+1)%20].second);
		double t2 = getr(pot[(i+1)%20].first, pot[(i+2)%20].first, pot[(i+1)%20].second, pot[(i+2)%20].second);
		//cout << t1 << " " << t2 << endl;
		if(fabs(t1 - 36) < 1e-4&&fabs(t2 - 81) < 1e-4) {
			print(true); return ;
		}
		if(fabs(t1 - 81) < 1e-4&&fabs(t2 - 36) < 1e-4) {
			print(false); return ;
		}
	}
}

int main()
{
	scanf("%d", &T);
	while(T--)
	{
		for(int i=0; i<20; i++)
			scanf("%lf%lf", &pot[i].first, &pot[i].second);
		solve();
	}
	return 0;
}

---

蒟蒻一只，欢迎指正