算法学习笔记之计算几何--平面凸包

Introduction

凸包（Convex Hull）是计算几何中的一类极其重要的问题，计算几何中的很多问题都可以转化为凸包问题来解决。

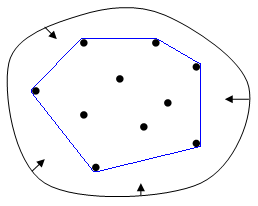
直观的来讲，凸包就像是在一块钉有若干个钉子的木板上撑开一根橡皮筋来讲所有钉子围起来一样。

构造凸包的算法可谓汗牛充栋，著名的有Gift wrapping（Jarvis March算法）, Graham scan, QuickHull, Divide and conquer, Incremental convex hull algorithm等。本文不可能面面俱到，在这里只选取一些具有代表性的算法来阐释凸包构造过程中的基本思想。

下面所介绍的算法中基本上都体现出了一个特征，就是利用问题的集合特质将问题一步步的转化，大事化小，小事化了，从而使问题得到解决。

基于极点的算法

极点

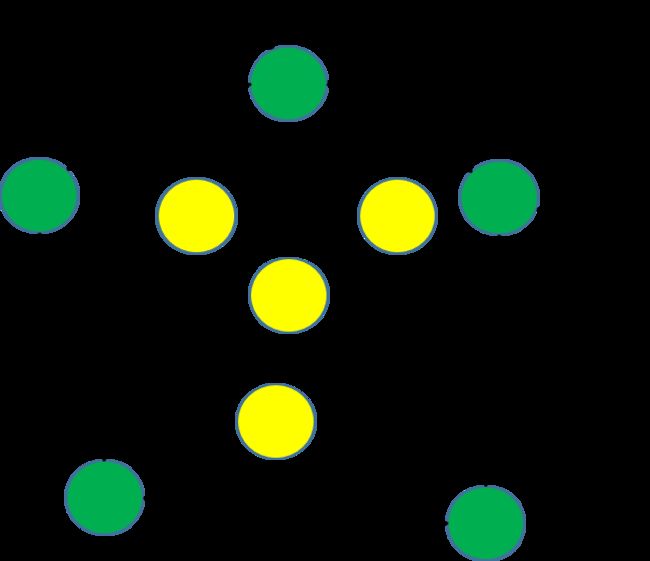
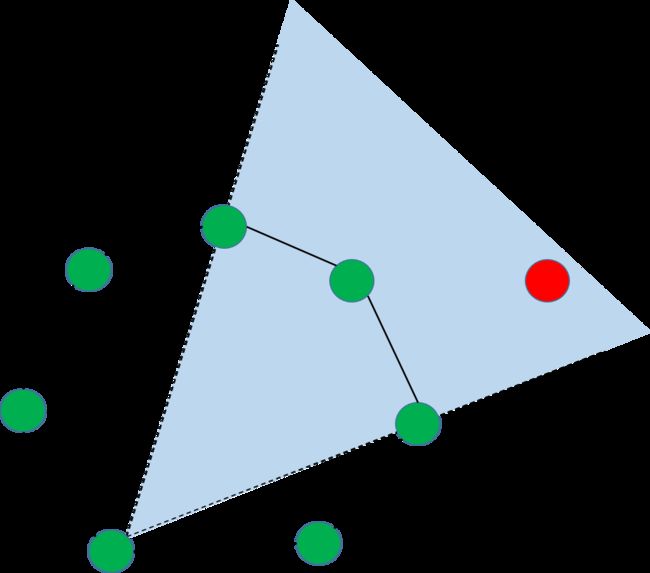
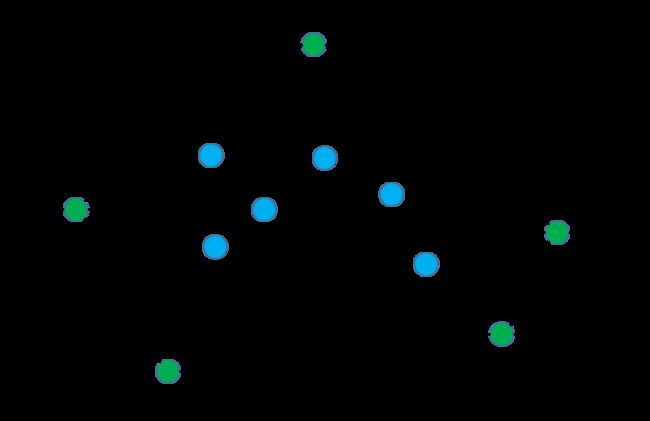
设 S 为平面点集，若存在一条经过点 p 的直线 l 使得除 p 点外所有的点都位于直线 l 的同一端，那么称点 p 为极点（Extreme Point）。否则称为非极点（Non-Extreme Point）。

如上图所示，直观的来讲，一个点是极点那么它一定就是凸包上的点。

构造策略

回忆一下冒泡排序的原理：

一个序列有序当且仅当每一个点都是有序的

同样的根据极点的概念我们有如下的凸包定义：

一个多边形为凸包当且仅当所有顶点都是极点

根据极点的定义我们可以想出一个很直接的凸包的构造算法：遍历每个点，检查是否为极点，如果是，就将它加入到凸包的集合中。这样，构造凸包的问题就被我们转化为了判断点是否为极点的问题，虽然离我们的目标还有一些距离，但已经前进了一大步。不过，我们还没有判断极点的算法。

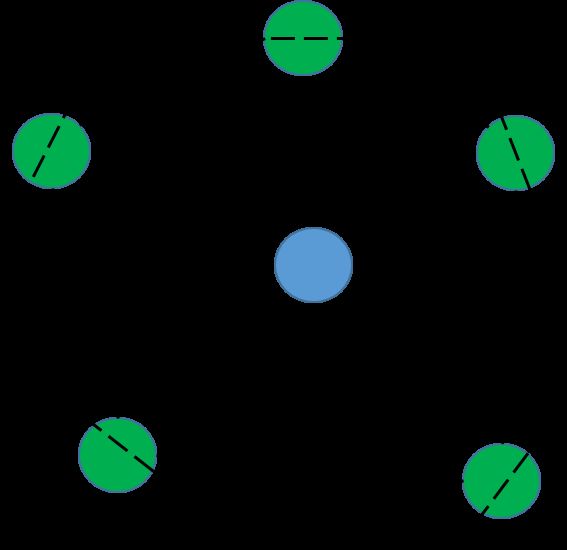
要判断一个点是不是极点其实很容易，它要不是极点，那么一定能找到三个点（从给定的点集中）将它包围起来。原因很简单，因为平面点集的凸包就是能将所有点包围起来的凸多边形，那么对于在凸包内部的点（不是极点的点）最少最少能从凸包上找到三个点将其围起来。于是就有：

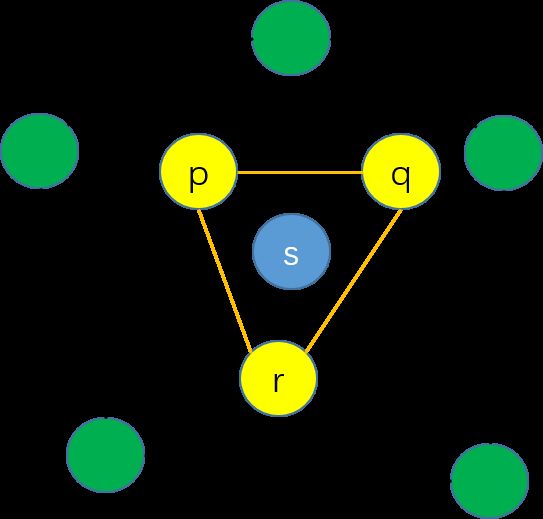
平面点集 S 中的一个点 s 不是极点当且仅当存在 {p,q,r}⊆S∖{s} 使得 s∈△(p,q,r) ，其中 △(p,q,r) 代表 p,q,r⊆S 组成的封闭三角形。

In-Triangle Test

虽然有了上面的判断极点的In-Triangle Test方法，但我们还无法马上给出一个实现，因为我们还不知道如何判断点是不是在三角形内。

要判断点是否在三角形内，需要用到一个计算几何中十分常用而重要的技术，叫做To-Left测试。

观察上面的图片，如果我们按照一定的顺序（如顺时针）检查三个点 p,q,r 构成的有向线段，就会发现无论是对于有向线段 rq 还是 qp 和 pr ，点 s 都位于它们的左边。

To-Left测试则可以完成这样的任务，对于点 (a,b,s) ，当 s 位于有向线段 ab 的左侧时，ToLeft(a, b, s)返回True，否则返回False。其利用的原理是叉积。

叉积（又称外积），其集合意义是向量 p1→ 和 p2→ 构成的平行四边形的有向面积。同时，当 p1→×p2→>0 时， p1→ 位于 p2→ 的顺时针方向，反之 p1→ 位于 p2→ 的逆时针方向。

我们现在可以给出To-Left测试的实现：

bool ToLeft(Point p, Point q, Point s){
    return p.x * q.y - p.y * q.x
        + q.x * s.y - q.y * s.x
        + s.x * p.y - s.y * p.x > 0;
}

完整算法

下面我们可以给出这个算法的完整实现：

mark all points of S as Extreme;

for each triangle(p,q,r):
    for each point s except (p,q,r):
        if s lies inside triangle(p,q,r):
            mark s as Non-Extreme;

枚举每个三角形需要 O(n3) 的时间，加上对每个三角形枚举每个点该算法总的时间复杂度为 O(n4) 。

基于极边的算法

刚才我们得到了一个可用的算法，但这近乎于brute-force，算法的时间复杂度过高以致于几乎不能用，为此我们不得不考虑更优的算法。

论及上面那个算法为什么这么慢的话，其原因便在于我们是基于极点来构造凸包的，而要判断极点又不得不枚举所有三角形，这样复杂度一下子就上去了，于是我们只有继续发掘看看凸包的几何性质，来找到一种更好的方法。

极边

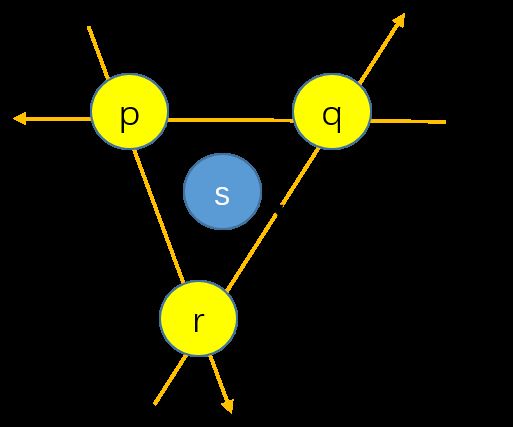
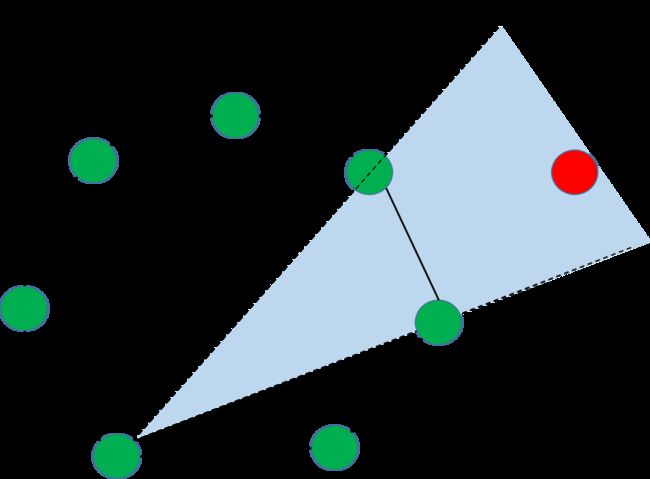
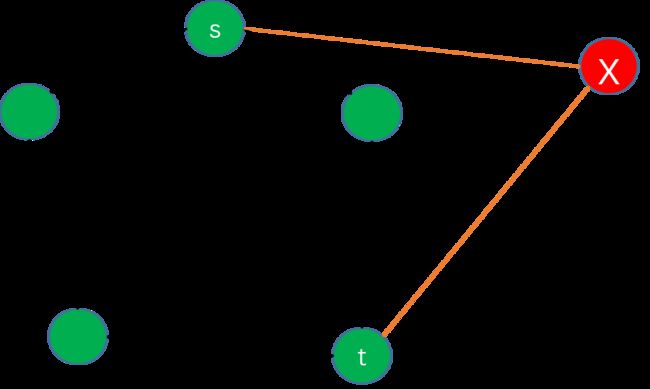
观察上图就可以发现，对于凸包上的每一条边，都将平面分成了两部分，并且其它所有的点都位于这条边的一侧。这些边称为极边。

对于 s,t∈S , e=(s,t) 为一条极边当且仅当 S∖{s,t} 中所有的点都位于 e 的同一侧。

根据上一节的经验，我们不难得出判断极边的方法：只要对每一个点进行一次To-Left测试即可。

完整算法

根据上面极边的定义我们可以将构造凸包的任务转化为判断极边。这样我们只需要遍历每一条边，然后检查它是否是极边即可。

下面是完整算法的伪代码：

let set of Extreme Edges empty;

for each segment pq:
    if points in S \ {p, q} lies to the same side of pq:
        then add pq to set of Extreme Edges;

按照上面的算法，枚举每条边需要 O(n2) 的时间，再对每个点进行检查总共的时间复杂度为 O(n3) 。

和上面的算法一样，这个算法的核心也是To-Left测试，只不过复杂度大大的下降了，这是一个长足的进步。

增量构造法 Incremental Construction

我们已经给出了两个算法，然而在实际应用中这两个算法的表现都不能让人满意。

在计算几何中常常会用到一种增量构造的技术，用增量法求凸包的思想是逐次的将点加入到凸包中，最终得到完整的凸包。这个算法的复杂度为 O(n2) 。

与插入排序类比

为了更好的理解这个算法，我们来回忆一下插入排序的原理。

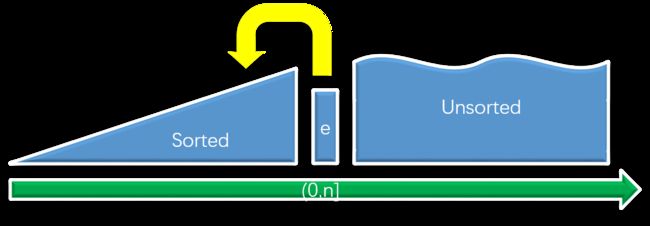
插入排序：不断地从未排序的元素中一个一个地取出元素插入到有序的序列中来构造有序序列

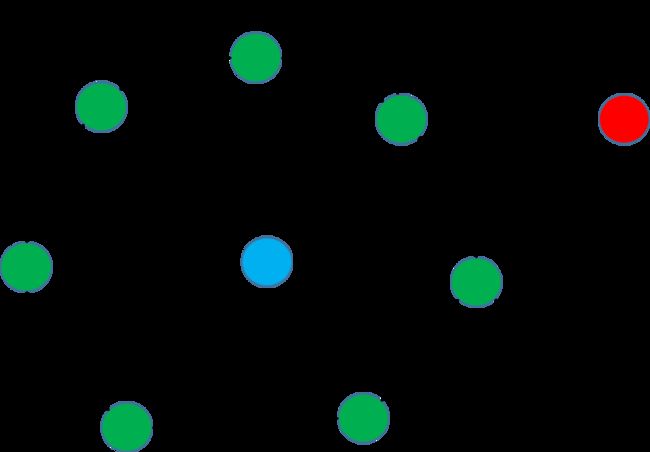
增量法就是从未检查的点中，每次取出一个点，检查它是否应该被加入到凸包中。

增量法：不断地地从未检查的点中一个一个地取出点加入到凸包中

不过，和插入排序不同的是，插入排序中有序序列只增不减，而凸包的增量法中有可能会出现以前被判定为凸包的点中在后来发现不属于凸包的情况，也就是说有增有减，如上图所示的情况。

要实现增量法，我们需要清楚两件事：

1. 如何判断点是否在凸包（凸多边形）内
2. 如何将新的点与已有凸包合并

我们先来讨论第一个问题。

In-Polygon Test(Binary Search)

据说判断点在凸多边形内是一道面试题，而且这个问题有一个 O(logn) 的算法，就是用二分法。

也许你会感到诧异，不过看了下面的图你应该就会明白。

如果我们给凸多边形上所有的点从 0−n 依次标上序号（逆时针），然后以 0,n/2 为有向线段对点 s 做To-Left测试，看点 s 落在有向线段的左边还是右边。

假设是右边，那我们再二分取 0,n/4 进行To-Left测试。

直到我们将范围缩小到点在 0,i 和 0,i+1 这两条有向线段之间的情况，那么我们只需要对 i,i+1 和点 s 做To-Left测试，就能判断点是否在凸多边形内了。由于用了二分法，每次判定都会收缩一半，所以可以在 O(logn) 的时间内完成。

这个算法看起来很美好不是吗？不过它并不适用于当前的情况。

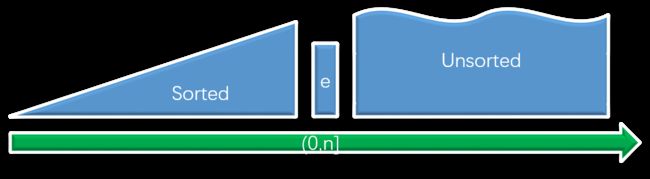
想想插入排序，你可能注意到可以对有序的部分用二分法，这样我们就可以在 O(logn) 的时间内确定新元素在有序序列中的位置了，而无需花 O(n) 的时间来一个一个找了。

不过这个想法有个致命的错误就是运用二分法的前提是我们得使用支持”按秩查询”的数据结构，如数组，然而这种数据结构的一个特点是插入十分低效。为了插入一个元素，我们不得不将后面所有元素都向后挪一位，这样最坏情况下时间复杂度高达 O(n) 。

所以说，即使你用 O(logn) 的时间进行定位，然而却不得不花 O(n) 的时间来插入，如果我们按一个一个找的方式来定位，并在找的过程中不断交换元素次序，这样的时间复杂度也是 O(n) ，而且实际表现可能比二分+插入更好。

同理，在构造凸包的过程中，若我们二分法判定一个点应当属于凸包后，我们将在插入点的过程中耗费大量时间，所以这种方法只适用于静态判断，对于动态的构造过程并不适用。

In-Polygon Test(Dynamically)

在上面的方法失败后，我们需要找到一种新的方法。

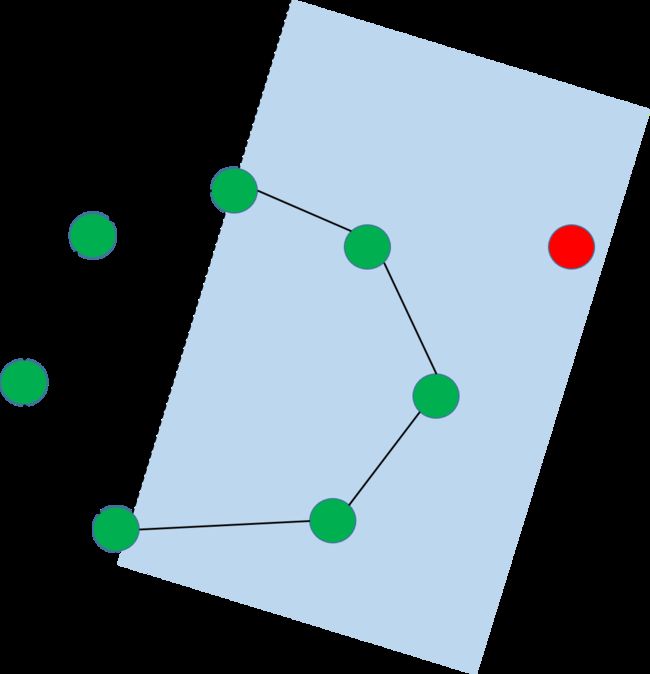
实际上，只要我们细心观察就会发现，如果一个点位于凸包的内部，那么我们按一定方向遍历每条边对点进行To-Left测试都会返回同样的结果，也就是说位于每条边的同一侧，而在外部的话至少会有一次To-Left测试返回不同的结果。

所以，判断点在凸多边形内最终归约为 n 次To-Left测试。

加入新的极点

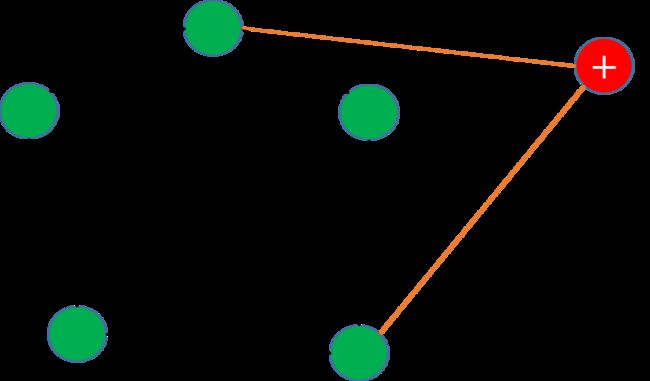
若点再多边形内部，我们直接舍弃这个点就行了，但若在多边形外部，我们就需要考虑如何将点加入到现有的凸包中。

从上面的图可以看出，当我们需要加入新的极点时，这个点会与凸包有两条切线，两个切点我们称为t,s，两条切线之间的那些边（称作ts）需要被剔除，而其他的（称作st）则需保留。

如果我们需要找出哪些点需要被删除时，那只需要找到两个切点即可。

注意观察凸包上某一点 si 的前驱点 pi ,后继点 ni 与 si 和新加入的点 snew 形成的有向线段的关系，你会发现，对于ts上的点， pi 和 ni 分别位于右边和左边，对于st上的点， pi 和 ni 分别位于左边和右边。而t点则 pi , ni 都位于左边，s点 pi , ni 都位于右边。

为此，我们只需要遍历一遍就能够找出t点和s点，从而找出需要删除的点。还有一个好消息就是这一步是可以和上面的判断点是否在多边形内合并的，因为如果点在多边形内，那么是不存在t和s的。

完整算法

下面给出完整算法：

for each point x:
    Traverse the convex hull and examine the     pattern of every vertex v;

        if it's pattern is LL/RR:
            then let s/t = v;

        if s and t are not found:
            then return;
        else:
            release ts and connect s and t with new point x;

由于每个点都要检查一遍凸包，故时间复杂度为 O(n2) 。

Jarvis March(Gift Wrapping)

Jarvis March算法（又称Gift Wrapping算法）是我们要介绍的第一个以人名命名的算法(●'◡'●)，这个算法的执行过程可以形象的看作是包装礼物。

直观理解

假想Jarvis March算法从点集中位置最低的那一个点（如果有多个点都同处于最低的那一条线，选最左边的那个，可以证明这个点一定属于凸包）开始把纸向右拉使其绷紧，然后让纸向逆时针方向旋转，直到碰到一个点，该点也必是凸包上的一个点。如此继续下去，直到回到初始点为止。

更准确的解释

当我们从 p0 开始时， p1 较其他点来说对于 p0 有着最小的极角，然后将 p1 加入到凸包中。对于 p1 来说， p2 有着最小的极角。一直到 p3 为止我们便构造好了凸包的右半部分。 p4 有着相对于 p3 的最小极角。这样我们就完成了整个凸包的构造。

Graham Scan

Graham Scan算法（葛立恒扫描法）是求解静态凸包的一种优秀的算法，它的时间复杂度在最坏的情况下为 O(nlogn) ，而在最好的情况下可以达到 O(n) 。

执行过程

Graham Scan算法的输入为点集 Q ，且 Q 包含的点的个数 ≥3 。在执行的过程中，Graham Scan算法会维护一个栈 S ，通过将点集 Q 的每一个点都入栈一次，不属于凸包的点最终会被弹出栈。在算法执行完毕后，留在栈 S 中的点就是完整的凸包。

我们先来看看伪代码：

let p0 be the point in Q with the minimum y-coordinate,or the leftmost such point in case of tie;

let (p1, p2, ... , pm) be the remainint points in Q,sorted by polar angle in counterclockwise order around p0;

if m < 2:
  return "convex hull is empty";
else:
  let S be an empty stack

s.push(p0);
s.push(p1);
s.push(p2);

for i = 3 to m:
  while the angle formed by points s.next_to_top, s.top and pi makes a nonleft turn:
    s.pop();
  s.push(pi);

return S;

下面来逐行讲解：

1. 第1行选出y坐标最小的点作为原点，如果有多个，则选取最左边的那个。可以证明，这个点一定是凸包上的点
2. 第3行将其他点按照相对于圆点的极角进行排序，在这里，我们并不是要将每个点的极角计算出来，而是采用叉积，这样可以避免复杂的运算和精度的损失。至于叉积为什么可以实现极角排序，是因为叉积有判定点与直线位置关系的功能。若点 a 比点 b 极角大，那么 a 一定位于直线 ob 逆时针方向
3. 第5行—第8行，对于少于三个点的情况直接判定凸包不存在，否则建立一个栈 S
4. 第10行—第12行，前3个点的凸包一定就是这三个点，这是分显然，因为三角形当然是凸的
5. 第14行—第17行是Graham Scan算法的核心执行过程，执行一个范围为 [3,m) 的 for 循环，在 for 循环内对每个点 pi 执行一个 while 语句，这个 while 语句检查栈 S 的头两个点所构成的边与点 pi 的位置关系，若点 pi 位于边的顺时针方向，则弹出栈 S 的头元素，直至点位于边的逆时针方向为止。 while 语句执行完成之后将点 pi 压入栈中。
6. 在前面的所有步骤执行完毕后，返回存放凸包结果的栈 S

正确性

对于Graham Scan算法算法的正确性，我们不妨采用数学归纳法证明。

首先，我们以前三个点为初始状态，不难得知前三个点构成的多边形一定就是前三个点的凸包。

接下来，我们假设算法已经完成了前 k 个点的凸包计算过程，我们止痒证明在对第 k+1 个点进行检查后能给出前 k+1 个点的凸包即可。

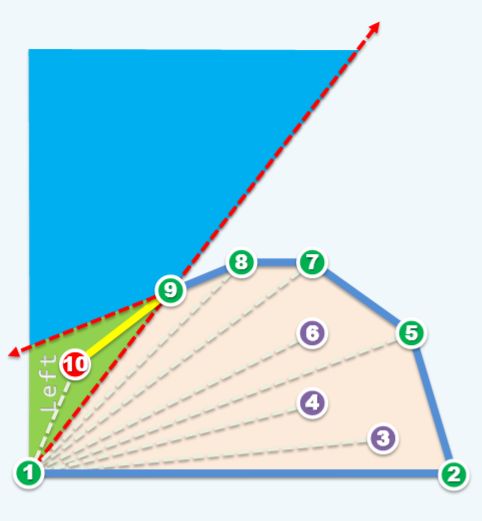
由于每一个点都经过了极角排序，所以点 pi 的位置一定会落在蓝色区域或是绿色区域中，对于落在绿色区域的情况，可以知道在加入点 pi 后，栈 S 所维护的点集仍然保持了凸性。

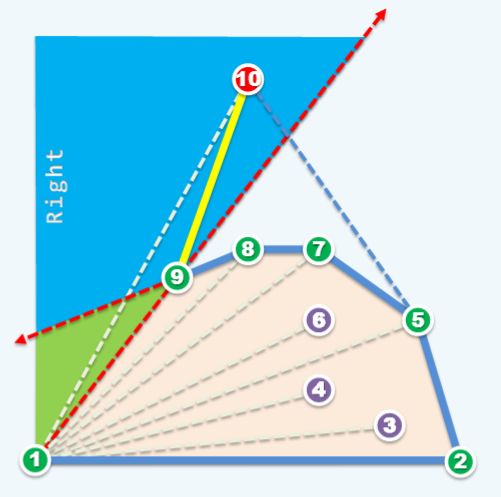
对于落在蓝色区域的情况则要复杂一些，因为在这个时候我们发现凸性被破坏了，也就是说以前我们加入了一些本不该属于凸包的点，这样我们需要执行回退。这个步骤会一直持续到栈 S 中的点集具有凸性为止，之后我们将点 pi 压入栈中，此时栈 S 所维护的点集仍然保持了凸性。原命题得证。

在最后还有一个小问题，就是在回退的过程中会出现栈 S 被弹出地只剩一个元素了吗？如果是这样那么在取出栈的头两个元素时将会引发Runtime Error。但实际上这并不会发生，因为点是按极角排序过的， 在栈 S 只剩2个点原点 p0 和栈顶元素 p1 的时候，点 pi 的极角一定大于点 p1 ，这时回退将结束。

代码

下面给出一个c++版本的实现，如果你的编译器不支持c++11，将lambda函数换成自定义的比较函数即可。

Point ori;

bool PolarCmp(Point a, Point b) {
  return DoubleCmp(Det(a - ori, b - ori)) > 0 || (DoubleCmp(Det(a - ori, b - ori) == 0 && DoubleCmp((a - ori).Norm() - (b - ori).Norm()) < 0));
}

void GrahamScan(vector &src, vector &dst) {
  // 找原点
  ori = src[0];
  for (int i = 1; i < src.size(); i++) {
    if (DoubleCmp(src[i].y - ori.y) < 0 || (DoubleCmp(src[i].y - ori.y) == 0 && DoubleCmp(src[i].x - ori.x) < 0)) {
      ori = src[i];
    }
  }

  // 极角排序
  sort(src.begin(), src.end(), PolarCmp);

  dst.clear();
  dst.push_back(src[0]);
  dst.push_back(src[1]);
  dst.push_back(src[2]);

  if (src.size() < 4) {
    return;
  }
  else {
    for (int i = 3; i < src.size(); i++) {
      while (Det(src[i] - dst[dst.size() - 2], dst.back() - dst[dst.size() - 2]) > 0) {
        dst.pop_back();
      }
      dst.push_back(src[i]);
    }
  }
}

Monotone Chain(Andrew’s algorithm)

Monotone Chain算法（又称Andrew算法）是一种Graham Scan算法的改进，其复杂度同样为 O(nlogn) ，不过与Graham Scan不同的是，Monotone Chain按照横坐标排序，这与极角排序相比起来更简单也更快，同时已经按横坐标排序的场合也更多。下面来介绍Monotone Chain的执行步骤。

执行步骤

• 首先，将点集 S={p1,p2,...,pn} 按横坐标优先纵坐标次优先排序
• 定义 p−− 为横坐标和纵坐标都最小的点， p−+ 为横坐标最小，纵坐标最大的点， p++ 为横坐标和纵坐标都最大的点， p+− 为横坐标最大，纵坐标最小的点，有时一个点同时满足上面的多个条件
• 创建一个栈 S
• 先构造下链 Ωmin 。
• 再构造上链 Ωmax 。
• 栈 S 中所存的就是完整的凸包

其中构造上下链的方式和Graham Scan如出一辙，都是检查新点和栈顶端两点构成的向量的位置关系。

实现

下面给出C++版本的代码：

// 输入点向量points,凸包向量ch
// 返回凸包顶点个数
void MonotoneChain(vector &points, vector &ch) {
  ch.resize(2 * points.size() + 5); // 调整大小以防越界
  sort(points.begin(), points.end()); // 按水平序排序
  points.erase(unique(points.begin(), points.end()), points.end()); // 去重，如果题意说明了没有重复点则可以不用这条语句

  int low_index = 0;
  int n = points.size();
  // 构造上凸包
  for (int i = 0; i < n; i++) {
    while (low_index > 1 && DoubleCmp(Det(ch[m - 1] - ch[m - 2], points[i] - ch[m - 2])) < 0) {
      low_index--;
    }
    ch[low_index++] = points[i];
  }

  // 构造下凸包
  int high_index = low_index;
  for (int i = n - 2; i >= 0; i--) {
    while (low_index > high_index && DoubleCmp(Det(ch[low_index - 1] - ch[low_index - 2], points[i] - ch[low_index - 2])) <= 0) {
      low_index--;
    }
    ch[low_index++] = points[i];
  }

  if (points.size() > 1) {
    ch.resize(low_index - 1);
  }
  else {
    ch.resize(low_index);
  }
}

凸包的应用

凸包是计算几何中的一类极其重要的问题，很多问题都可以转化为凸包来解决，下面我们来看一些凸包的应用。

最远点对—旋转卡壳

对于一个平面点集我们要如何求出其中的最远点对呢？要解决这个问题需要借助旋转卡壳算法，旋转卡壳算法用于求凸包的直径，即凸包上最远的点对的距离。而平面点集最远点对一定是位于凸包上的，所以我们对点集求凸包再使用旋转卡壳算法就能求出最远点对。

要理解旋转卡壳算法我们可以想象有一对平行的直线从两边向中间靠拢将凸包夹住，这时直线会与凸包至少有两个交点，在交点有两个的情况下这两个点称为对踵点，凸包的直径就是对踵点对中距离最大的那一对的距离。

按照上面的描述来写旋转卡壳的代码显然是不切实际的，因为我们不可能枚举所有可能的直线来求它与凸包的交点，为此，我们继续观察。假设已经有一对直线将凸包夹住了，并假设交点数为2，我们可以将直线对进行旋转使其与凸包上的一条边重合，我们发现在旋转的过程中对踵点并没有发生变化，为此问题就转化为了对每个点找距离最远的边了。但如果直接枚举复杂度是 O(n2) ，这样就和对点进行两两枚举没有区别了。但如果继续想想不难发现如果我们将直线对继续进行旋转就能找到新的点—边对，这样就能找到新的对踵点对。

代码如下：

// 返回凸包直径的平方
int RotateCaliper(vector &ch) {
  int diameter2 = 0;
  ch.push_back(ch[0]);
  for (int i = 0, j = 1; i < ch.size() - 1; i++) {
    while (DoubleCmp(Cross(ch[i + 1] - ch[i], ch[j] - ch[i]) - Cross(ch[i + 1] - ch[i], ch[j + 1] - ch[i])) < 0) {
      j = (j + 1) % (ch.size() - 1);
    }
    diameter2 = max(diameter2, max((int)((ch[i] - ch[j]).Norm2() + 0.5), (int)((ch[i + 1] - ch[j + 1]).Norm2() + 0.5)));
  }
  return diameter2;
}