Poj 3277 City Horizon - 线段树

题目大意：在水平直线上给定一组矩形，这些矩形的底边在同一水平线上，求这些矩形占据的面积。

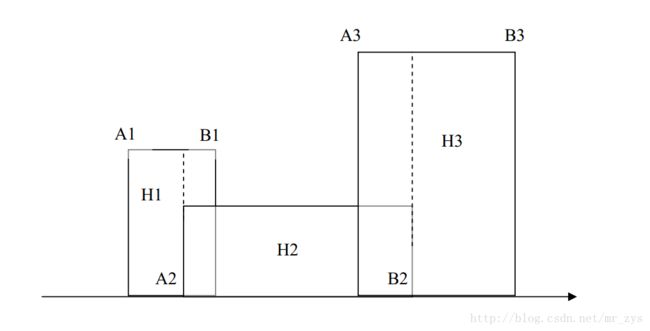
题目分析：很显然，这些矩形的长和高都不一样，还会有重合的区域。如何求这些矩形的面积呢？画个图就知道了。

                    

                 对于上图给定的三个矩形，最快的求面积的方法就是将每条线段乘以当前该条线段对应的最高的高。譬如 A1-B1对应的最高的是H1，B1-A3对应的是H2，A3-B3对应的是H3，可以得到面积A = H1*(B1-A1)+H2*(A3-B1)+H3*(B3-A3)。

                 这样就有思路了，将每个矩形的长看做是一条线段，然后更新这些线段上面的权值（高）。这样就是区间更新了，可以用线段树做。

                 首先建树，然后成段的更新树上结点的信息。这里建树要注意一下。注意观察上面求面积的表达式。

                 数据比较大，所以要离散化了。

代码：

#include 
#include 
using namespace std;

#define maxn 40400
int max_h[maxn*10];
int line[maxn<<2];
struct buildings
{
    int a;
    int b;
    int h;
} B[maxn];
void build(int l,int r,int rt)
{
    max_h[rt] = 0;
    if(l + 1== r) return;
    int mid = (l + r) >> 1;
    build(l,mid,rt<<1);
    build(mid,r,rt<<1|1);
}
void update(int l,int r,int rt,int L,int R,int h)
{
    if(line[l] == L && line[r] == R) //如果在这里推出递归的话，rt的子孙结点都不会被更新，所以在下面的solve函数里有处理
    {
        max_h[rt] = max(max_h[rt],h);
        return ;
    }
    int m = (l + r) >> 1;
    int mid = line[m];
    if(R <= mid) update(l,m,rt<<1,L,R,h);
    else if(L >= mid) update(m,r,rt<<1|1,L,R,h);
    else
    {
        update(l,m,rt<<1,L,mid,h);
        update(m,r,rt<<1|1,mid,R,h);
    }
}
long long solve(int l,int r,int rt,int h)
{
    //如果rt结点的值大，那么rt的子孙结点都是该值
    if( h > max_h[rt]) max_h[rt] = h;
    if(l + 1 == r) return (long long) (line[r] - line[l]) * max_h[rt];
    int mid = (l + r) >> 1;
    return solve(l,mid,rt<<1,max_h[rt]) + solve(mid,r,rt<<1|1,max_h[rt]);
}
int main()
{
    int n,cnt;
    scanf("%d",&n);
    cnt = 0;
    for(int i = 0; i < n; i++)
    {
        scanf("%d%d%d",&B[i].a,&B[i].b,&B[i].h);
        line[++cnt] = B[i].a;
        line[++cnt] = B[i].b;
    }
    sort(line+1,line+1+cnt);
    cnt = unique(line+1,line+1+cnt) - line -1;
    build(1,cnt,1);
    for(int i = 0; i < n; i++) update(1,cnt,1,B[i].a,B[i].b,B[i].h);
    printf("%lld\n",solve(1,cnt,1,0));
    return 0;
}