2020牛客多校（第九场）
A-Groundhog and 2-Power Representation
题意
- 求表达式的值
- 只有2 0 + ( ) 组成
- 2(0)表示2的0次
思路
- 用python写非常方便
- 写个x(i)函数表示2的幂次，然后将字符串中的"2("字符替换成"x("
- 最后调用eval函数将字符串变成有效的表达式求值并返回结果
AC代码
Python真是个好东西def x(a):
return 2**a
str = input()
str = str.replace("2(","x(")
print(eval(str))
E-Groundhog Chasing Death
题意
- 求
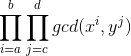mod 998244353的结果
思路
- 唯一分解定理：任何数都可以表示成质因子幂次相乘的形式。
,
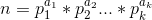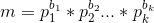
- gcd（n，m）=
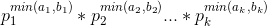
- 因为
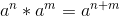，所以设p是n,m共有的质因子，k1和k2是n，m对于p的幂次，则就是求解（p是n,m共有的质因子） - 优化一个for，找到k1*i和k2*j的零界点sh，sh=k1*i/k2，此时j在sh左边的时候，min总是取k1*i，由于此时的i不变，直接乘数量就好了；j在sh右边的时候,min总是取k2*j，由于j在变，不过就是对等差数列求和。
AC代码
真读题五分钟 代码半小时分钟 优化三小时 没想到欧拉降幂太难受了
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include // pair
#include
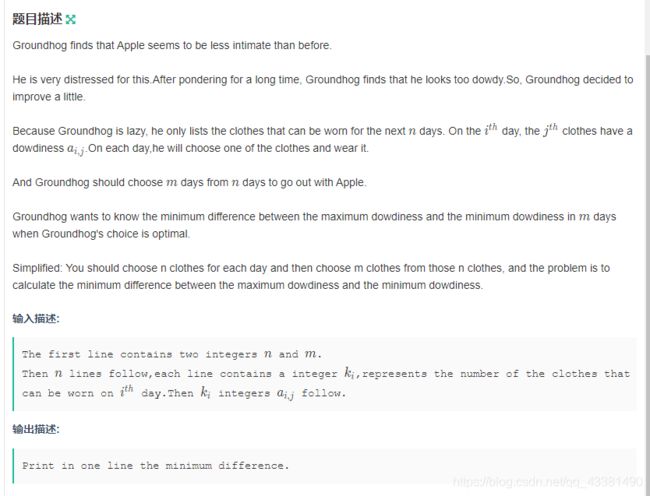
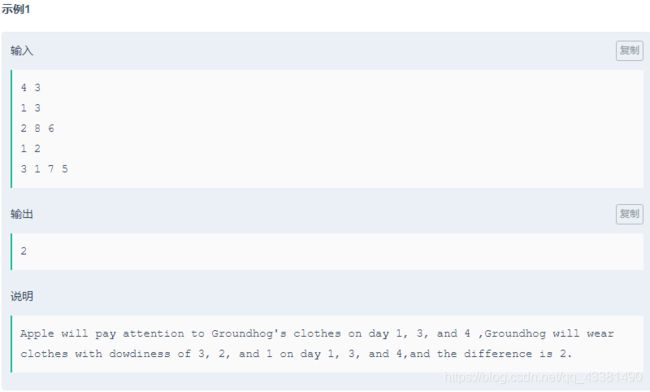
F-Groundhog Looking Dowdy
题意
- 给定n天，每天生产ki件衣服，选择m件来自不同天的衣服，求最大价格和最小价格的最小差值
- 数据范围：1<=aij<=1e9,1<=n<=1e6,1<=m<=n,sum of clothes<=2e6,k>=1
思路
- 尺取法。
- 首先结构体存衣服生产日期和价格，按照价格从小到大排序。
- l，r分别是左右端点，当区间内衣服不同生产日期数num没有超过m时，r++；
- 等于m时，更新左右端点价格差值的最小值 ，l++，直到num
AC代码
（这题每天取最小的也能水过去）
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf = 0x3f3f3f3f;
const double pi = acos(-1.0);
const ll mod = 998244353;
#define ios std::ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);
ll quickpow(ll a, ll b)
{
ll ret = 1;
while (b != 0)
{
if (b & 1)
ret = ret * a % mod;
b >>= 1;
a = a * a % mod;
}
return ret % mod;
}
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
} //最大公约数
ll exgcd(ll l, ll r, ll &x, ll &y)
{
if (r == 0)
{
x = 1;
y = 0;
return l;
}
else
{
ll d = exgcd(r, l % r, y, x);
y -= l / r * x;
return d;
}
} //拓展gcd
long long lcm(long long a, long long b)
{
return a * (b / gcd(a, b));
} //最小公倍数
ll qmul(ll a, ll b, ll m)
{
ll ans = 0;
ll k = a;
ll f = 1; //f是用来存负号的
if (k < 0)
{
f = -1;
k = -k;
}
if (b < 0)
{
f *= -1;
b = -b;
}
while (b)
{
if (b & 1)
ans = (ans + k) % m;
k = (k + k) % m;
b >>= 1;
}
return ans * f;
} //快乘 爆ll时用
/*
ll china(ll n, ll *a, ll *m)
{
ll M = 1, y, x = 0, d;
for (ll i = 1; i <= n; i++)
M *= m[i];
for (ll i = 1; i <= n; i++)
{
ll w = M / m[i];
exgcd(m[i], w, d, y); //m[i]*d+w*y=1
x = (x + y * w * a[i]) % M;
}
return (x + M) % M;
} //中国剩余定理
ll mod_inverse(ll a, ll m)
{
ll x, y;
if (exgcd(a, m, x, y) == 1) //ax+my=1
return (x % m + m) % m;
return -1; //不存在
} //求a关于m的乘法逆元
*/
/*欧拉素数筛*/
/*void Prime(){
const int maxn= 1e5+5;
int prime[maxn];//素数存放位置
int visit[maxn];
memset(visit,0,sizeof(visit));
memset(prime,0,sizeof(prime));
for (int i = 2;i <= maxn; i++) {
if (!visit[i]) {
prime[++prime[0]] = i;
}
for (int j = 1; j <=prime[0] && i*prime[j] <= maxn; j++) {
visit[i*prime[j]] = 1;
if (i % prime[j] == 0) {
break;
}
}
}
}
*/
/*
const int MAXN = 1e5 + 10;
int g[MAXN];
int d[MAXN];
int find(int a)
{
if (g[a] == a) return a;
return g[a] = find(g[a]);
}
inline void bind(int a,int b)
{
int x = find(a), y = find(b);
if (d[x] >= d[y]) { // 如果a的 根的子树深度 比b的 根的子树深度 大，那a的根继续做根
g[y] = x; // 改变b节点的根的根为a的根
if (d[x] == d[y]) { // 俩根深度一样
if (x != y) d[x] ++; // 作为a的根，自然子树的深度++
}
} else g[x] = y;
}
void init(int n)
{
for(int i=0;i<=n;i++) {
g[i] = i; // 每个种类初始状态只有自己一个点
d[i] = 1; // 初始化秩
}
}
//并查集
*/
const int maxn=1e6+5;
pair a[maxn<<1];
int cmp(pair x,pair y){
return x.second
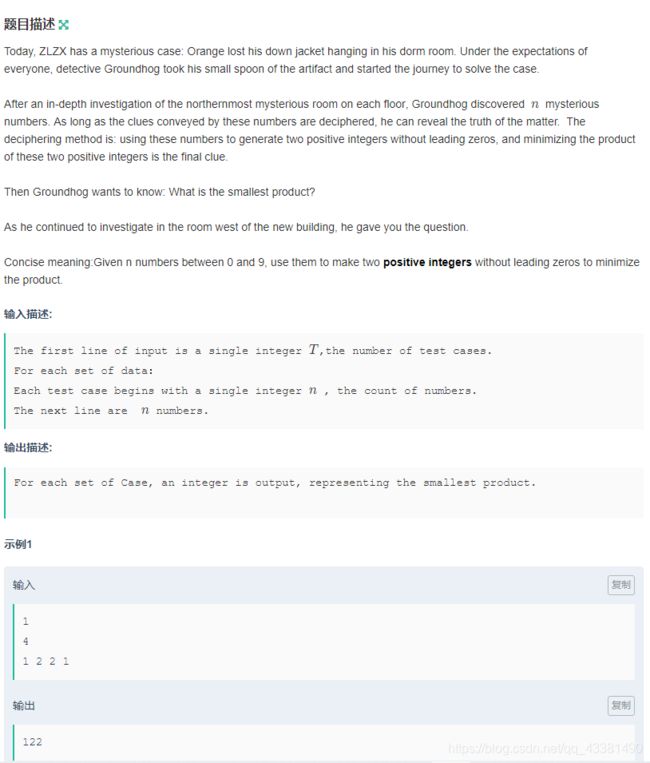
I-The Crime-solving Plan of Groundhog
题意
- 给一个序列仅包含数字，让你将其打乱次序并组合成两部分，使这两部分组成的数字相乘得到的结果最小
- 不允许任何一部分组成的数字包含前导零
思路
- 大数运算。 两位乘两位的数字一定比一位乘三位的数字大
- 组合成1位数乘n-1位数
- 1位数是除零外最小的
- n-1位数是第一位是除零最小，接着是从小到大加入
- 然后是模拟乘法运算。
AC代码
（本来想手动string模拟的 但是队友拉了个板子）
#include
#include
#include
#include
#include
using namespace std;
#define MAXN 9999
#define MAXSIZE 10
#define DLEN 4
class BigNum {
private:
int a[100005]; //可以控制大数的位数
int len; //大数长度
public:
BigNum(){ len = 1; memset(a, 0, sizeof(a)); } //构造函数
BigNum(const int); //将一个int类型的变量转化为大数
BigNum(const char*); //将一个字符串类型的变量转化为大数
BigNum(const string); //将一个string类型的变量转化为大数
BigNum(const BigNum &); //拷贝构造函数
BigNum &operator=(const BigNum &); //重载赋值运算符，大数之间进行赋值运算
friend istream& operator>>(istream&, BigNum&); //重载输入运算符
friend ostream& operator<<(ostream&, BigNum&); //重载输出运算符
BigNum operator + (const BigNum &) const; //重载加法运算符，两个大数之间的相加运算
BigNum operator - (const BigNum &) const; //重载减法运算符，两个大数之间的相减运算
BigNum operator * (const BigNum &) const; //重载乘法运算符，两个大数之间的相乘运算
BigNum operator / (const int &) const; //重载除法运算符，大数对一个整数进行相除运算
BigNum operator ^ (const int &) const; //大数的n次方运算
int operator % (const int &) const; //大数对一个int类型的变量进行取模运算
bool operator > (const BigNum & T)const; //大数和另一个大数的大小比较
bool operator > (const int & t)const; //大数和一个int类型的变量的大小比较
void print(); //输出大数
};
BigNum::BigNum(const int b){ //将一个int类型的变量转化为大数
int c,d = b;
len = 0;
memset(a, 0, sizeof(a));
while(d > MAXN)
{
c = d - (d / (MAXN + 1)) * (MAXN + 1);
d = d / (MAXN + 1);
a[len++] = c;
}
a[len++] = d;
}
BigNum::BigNum(const char*s){ //将一个字符串类型的变量转化为大数
int t, k, index, l, i;
memset(a, 0, sizeof(a));
l = strlen(s);
len = l / DLEN;
if(l % DLEN)
len++;
index = 0;
for(i = l - 1;i >= 0; i -= DLEN){
t = 0;
k = i - DLEN + 1;
if(k < 0) k = 0;
for(int j = k; j <= i; j++)
t = t * 10 + s[j] - '0';
a[index++] = t;
}
}
BigNum::BigNum(const string s){
int t, k, index, l, i;
memset(a, 0, sizeof(a));
l = s.size();
len = l / DLEN;
if(l % DLEN)
len++;
index = 0;
for(i = l - 1;i >= 0; i -= DLEN){
t = 0;
k = i - DLEN + 1;
if(k < 0) k = 0;
for(int j = k; j <= i; j++)
t = t * 10 + s[j] - '0';
a[index++] = t;
}
}
BigNum::BigNum(const BigNum & T) : len(T.len){ //拷贝构造函数
int i;
memset(a, 0, sizeof(a));
for(i = 0 ; i < len ; i++)
a[i] = T.a[i];
}
BigNum & BigNum::operator=(const BigNum & n){ //重载赋值运算符，大数之间进行赋值运算
int i;
len = n.len;
memset(a, 0, sizeof(a));
for(i = 0 ; i < len ; i++)
a[i] = n.a[i];
return *this;
}
istream& operator>>(istream & in, BigNum & b){ //重载输入运算符
char ch[MAXSIZE*4];
int i = -1;
in >> ch;
int l = strlen(ch);
int count = 0, sum = 0;
for(i = l - 1; i >= 0; )
{
sum = 0;
int t = 1;
for(int j = 0; j < 4 && i >= 0; j++, i--, t *= 10)
sum += (ch[i] - '0') * t;
b.a[count]= sum;
count++;
}
b.len = count++;
return in;
}
ostream& operator<<(ostream& out, BigNum& b){ //重载输出运算符
int i;
cout << b.a[b.len - 1];
for(i = b.len - 2; i >= 0; i--)
{
cout.width(DLEN);
cout.fill('0');
cout << b.a[i];
}
return out;
}
BigNum BigNum::operator+(const BigNum & T) const{ //两个大数之间的相加运算
BigNum t(*this);
int i, big; //位数
big = T.len > len ? T.len : len;
for(i = 0 ; i < big ; i++)
{
t.a[i] += T.a[i];
if(t.a[i] > MAXN)
{
t.a[i + 1]++;
t.a[i] -= MAXN+1;
}
}
if(t.a[big] != 0)
t.len = big + 1;
else
t.len = big;
return t;
}
BigNum BigNum::operator-(const BigNum & T) const{ //两个大数之间的相减运算
int i, j, big;
bool flag;
BigNum t1, t2;
if(*this > T){
t1 = *this;
t2 = T;
flag = 0;
}
else{
t1 = T;
t2 = *this;
flag = 1;
}
big = t1.len;
for(i = 0 ; i < big ; i++){
if(t1.a[i] < t2.a[i]){
j = i + 1;
while(t1.a[j] == 0)
j++;
t1.a[j--]--;
while(j > i)
t1.a[j--] += MAXN;
t1.a[i] += MAXN + 1 - t2.a[i];
}
else
t1.a[i] -= t2.a[i];
}
t1.len = big;
while(t1.a[len - 1] == 0 && t1.len > 1){
t1.len--;
big--;
}
if(flag) t1.a[big-1]=0-t1.a[big-1];
return t1;
}
BigNum BigNum::operator*(const BigNum & T) const{ //两个大数之间的相乘运算
BigNum ret;
int i, j, up;
int temp, temp1;
for(i = 0 ; i < len ; i++)
{
up = 0;
for(j = 0 ; j < T.len ; j++)
{
temp = a[i] * T.a[j] + ret.a[i + j] + up;
if(temp > MAXN)
{
temp1 = temp - temp / (MAXN + 1) * (MAXN + 1);
up = temp / (MAXN + 1);
ret.a[i + j] = temp1;
}
else
{
up = 0;
ret.a[i + j] = temp;
}
}
if(up != 0)
ret.a[i + j] = up;
}
ret.len = i + j;
while(ret.a[ret.len - 1] == 0 && ret.len > 1)
ret.len--;
return ret;
}
BigNum BigNum::operator/(const int & b) const{ //大数对一个整数进行相除运算
BigNum ret;
int i, down = 0;
for(i = len - 1 ; i >= 0 ; i--)
{
ret.a[i] = (a[i] + down * (MAXN + 1)) / b;
down = a[i] + down * (MAXN + 1) - ret.a[i] * b;
}
ret.len = len;
while(ret.a[ret.len - 1] == 0 && ret.len > 1)
ret.len--;
return ret;
}
int BigNum::operator %(const int & b) const{ //大数对一个int类型的变量进行取模运算
int i, d = 0;
for (i = len-1; i>=0; i--)
{
d = ((d * (MAXN+1))% b + a[i])% b;
}
return d;
}
BigNum BigNum::operator^(const int & n) const{ //大数的n次方运算
BigNum t,ret(1);
int i;
if(n < 0) exit(-1);
if(n==0) return 1;
if(n==1) return *this;
int m = n;
while(m>1) {
t = *this;
for(i = 1; i<<1 <= m; i<<=1)
t = t * t;
m -= i;
ret = ret * t;
if(m == 1)
ret = ret * (*this);
}
return ret;
}
bool BigNum::operator>(const BigNum & T) const{ //大数和另一个大数的大小比较
int ln;
if(len > T.len)
return true;
else if(len == T.len){
ln = len - 1;
while(a[ln] == T.a[ln] && ln >= 0)
ln--;
if(ln >= 0 && a[ln] > T.a[ln])
return true;
else
return false;
}
else
return false;
}
bool BigNum::operator >(const int & t) const { //大数和一个int类型的变量的大小比较
BigNum b(t);
return *this>b;
}
void BigNum::print(){ //输出大数
int i;
cout << a[len - 1];
for(i = len - 2 ; i >= 0 ; i--){
cout.width(DLEN);
cout.fill('0');
cout << a[i];
}
cout << endl;
}
int main(){
int tt;
scanf("%d", &tt);
while(tt--){
int n;
scanf("%d", &n);
int a[10] = {0};
for(int i = 0; i < n; i ++){
int p;
scanf("%d", &p);
a[p]++;
}
string s1="",s2="";
for(int i = 1; i < 10; i ++){
if(a[i]){
a[i]--;
s1+=(i+'0');
break;
}
}
for(int i = 1; i < 10; i ++){
if(a[i]){
a[i]--;
s2 += (i+'0');
break;
}
}
for(int i = 0; i < 10; i ++){
for(int j = 0; j < a[i]; j ++){
s2 += (i+'0');
}
}
BigNum b(s1);
BigNum bb(s2);
b = b * bb;
b.print();
}
return 0;
}
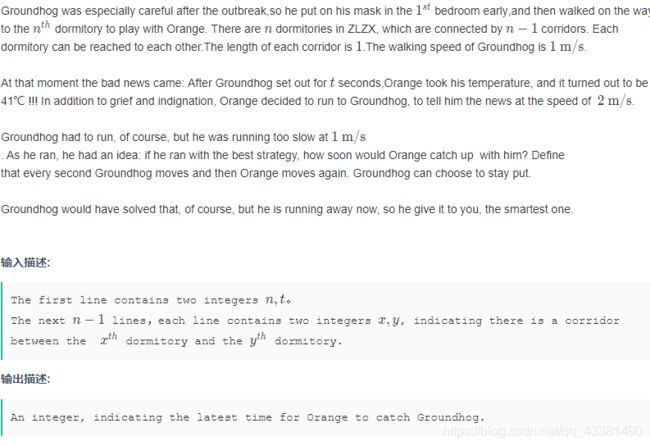
K-The Flee Plan of Groundhog
题意
- 有n个结点，n-1条边，小A从1号结点出发前往n号结点看望小B，每秒能走一条路
- t秒钟之后小B从n结点出发，来追小A，每秒能走两条路
- 问最迟要多久才能相遇
思路
- 以n结点为根dfs递归建树。
- n个结点，n-1条边，说明这是一棵树，所以小A从1出发去n只有一条路径，t秒之后小A的位置可以计算出来 。
- 求的是最迟相遇时间，那么小A就要远离小B，往树的深处跑，那么就有两种情况。
- 第一种情况，小A还没到树的最深处就被小B追上了。因为小B速度是小A的两倍，那么追逐时间其实就是两人的深度之差。
- 第二种情况，小A到最深处等小B。那么追逐时间就是小B到达最深处的时间。
AC代码
#include
#define inf 0x3f3f3f3f
// #include
#define ll long long
#define T int t;scanf("%d", &t);while(t--)
using namespace std;
// using namespace std::tr1;
const int mod = 1e9 + 7;
const int N = 1e7 + 10;
int n, t;
int node;
int cnt;
int head[N];
int t1[N];
int ans = 0;
struct ed{
int to, ne;
}e[N<<4];
void add(int u, int v){
e[cnt].to = v;
e[cnt].ne = head[u];
head[u] = cnt++;
}
int dfs(int u,int f,int step){
if(u == n) return 1;
for(int i = head[u]; i != -1; i = e[i].ne){
int v = e[i].to;
if(v==f) continue;
int m = dfs(v,u,step+1);
if(step == t && m==1){
node = u;
}
if(m==1) return 1;
}
return 0;
}
void dfs1(int u, int f,int step, int op){
t1[u] = step;
for(int i = head[u]; i != -1; i = e[i].ne){
int v = e[i].to;
if(v==f) continue;
if(op)
dfs1(v,u,step+1,0);
else
dfs1(v,u,step,1);
}
}
void dfs2(int u,int f, int step){
ans = max(ans,t1[u]);
for(int i = head[u]; i != -1; i = e[i].ne){
int v = e[i].to;
if(v==f) continue;
if(step+1 " << t1[i] << endl;
// ans = ceil(ans/2.0);
printf("%d\n", ans);
return 0;
}
/*
9 2
1 8
8 2
2 3
2 4
2 7
7 9
4 5
5 6
*/