PageRank 页面排名算法
前言
写这篇文章主要是为了后面的TextRank算法做铺垫,所以我会非常简短的描述,可能读者理解起来有一点费劲。
PageRank
佩奇排名(PageRank),又称网页排名、谷歌左侧排名、PR等,是Google公司所使用的对其搜索引擎搜索结果中的网页进行排名的一种算法。是Google创始人拉里·佩奇和谢尔盖·布林于1997年构建早期的搜索系统原型时提出的链接分析算法,
- PageRank是Google用于用来标识网页的等级/重要性的一种方法,是Google用来衡量一个网站的好坏的唯一标准。
- Google通过PageRank来调整结果,使那些更具“等级/重要性”的网页在搜索结果中另网站排名获得提升,从而提高搜索结果的相关性和质量。
当然这是早期算法,现在应该不用了。主要思想是:
- 数量假设:如果越多的网页指向网页A,即网页A的入链数量越多,则该网页A越重要
- 质量假设:一个网页是重要的,那么它指向的网页也是重要的
基于这两个假设建立模型,这是一张图模型,每一个页面都是一个节点,节点之间有带方向的直线表明我指向你,来一张图吧:
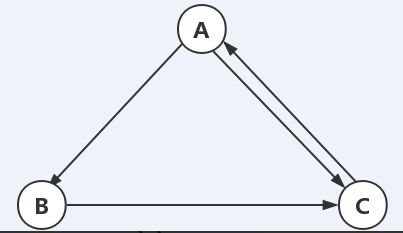
模型是图模型,那么重要性分数怎么计算?根据上述中心思想如何实现呢?简单一点来算,你自己也能想出来:
- 1、A指向C,C重要性加1,也可以说每个节点一开始默认都是1,指向一个节点,这个节点重要性加1
- 2、上图中:C重要性分数2,A重要性分数1,B重要性分数1
似乎也是这么回事,这个计算方式还挺像样的,但是,好像跟我们的假设不太一样:
- C那么重要,指向A,说明A也很重要,怎么给A的分数就是1了,跟A给B的分数一样?
- 有的节点有两个指向,比如A节点同时指向B、C节点,但是权重都是1,似乎指向的多少都不影响给的权重。
有的人就想着不能这么算,他提出:
- 一个节点指向其他节点,那么它的分数应该平均给其他节点,而不是每次都是给1
你不能是无限分数呀,你指向那么多节点,都给1,那么相当于你这个节点有无穷的分数,无限节点诞生? - 像上图那样循环 B − > C − > A − > B B->C->A->B B−>C−>A−>B,这样循环计算分数下去,什么时候才结束呀?
依据收敛准则,收敛到一定的分数就停止,不再计算。
所以改进一下:
- 第一轮开始:默认都是1
B节点指向C:+1,C指向A:+1,A指向B、C,B:+0.5,C:+0.5
最终,B:0.5,A:1,C:1.5 - 第二轮开始,根据第一轮的结果继续
最终,B:1,A:1.5,C1 - 再来第三轮,后面就不继续了
这里要注意一点:不能拿已经算好的A的权重再参与到当前轮数的计算里面,很多博客都是把当前的计算结果参与到当前轮数的其他节点的计算,这是错误的,必须注意一下。
所以我们抽象出函数就是:
P R ( p i ) = ∑ p j ( P R ( p j ) L ( p j ) ) PR(p_i) = \sum_{pj}(\frac{PR(p_j)}{L(p_j)}) PR(pi)=pj∑(L(pj)PR(pj))
参数解释:
- p j pj pj:是 p i pi pi的入链,C有A、B指向,所以要遍历A、B
- L ( p j ) L(p_j) L(pj):表示 p j pj pj的出链的个数,A有两个出链,所以等于2
这个公式不太好理解,我重写一个。
P R ( p i ) = ∑ p j ∈ E ( p i ) ( P R ( p j ) L e n ( p j ) ) PR(p_i) = \sum_{pj \in E(pi)}(\frac{PR(p_j)}{Len(pj)}) PR(pi)=pj∈E(pi)∑(Len(pj)PR(pj))
用矩阵来表示更好的理解,我们就拿上述的图来做关系矩阵:
P 3 ∗ 3 = 0 0 1 1 2 0 0 1 2 1 0 \begin{aligned} \mathbb{P}^{3*3}=\begin{array} {|cccc|} 0&0&1\\ \frac{1}{2}&0&0\\ \frac{1}{2}&1&0\\ \end{array} \end{aligned} P3∗3=02121001100
行坐标、列坐标都是A、B、C,我们从两个角度来理解:
- 按列理解:每一列表示,列节点到各个节点的关联,第一列列节点是A,A到B、C,所以B行是 1 2 \frac{1}{2} 21,C同理,这一列数据相加等于1,代表其他节点占A节点的占比
- 按行理解:每一行表示当前节点的权重受其他节点的影响,也可以是权重计算公式,比如第一行,行节点是A, A = C A=C A=C,第三行节点是C, C = 1 2 A + B C=\frac{1}{2}A+B C=21A+B,C的计算受A、B的影响
上述矩阵是节点之间的关系矩阵,怎么计算得到最终的分数呢?我们还是认为给一个默认值,乘以这个关系矩阵,会得到一个新的分数,这样
- 1、默认值都给1,记作 V 0 V_0 V0
- 2、利用公式 V i = P ∗ V i − 1 V_i=P*V_{i-1} Vi=P∗Vi−1来迭代计算, V 1 = P ∗ V 0 V_1=P*V_{0} V1=P∗V0, V 2 = P ∗ V 1 V_2=P*V_{1} V2=P∗V1
- 3、这样迭代计算,直到上一轮与下一轮的差值小于某个值,即 V i − V i − 1 < θ V_i-V_{i-1}<\theta Vi−Vi−1<θ,这样就收敛来,就可以终止
以上就是大致的流程,其实还可以思考为什么会收敛?这个也要证明,不然永远都不会收敛。
改进
其实我觉得有一些问题,
- 那就是为什么每次都是收敛?
- 一个节点不跟其他任何节点关联,那么这个节点就是0,但是用户可能通过URL 拼接自己去访问其他网页节点
- 另一个就是这个网页节点自己引用自己,这样将最终导致概率分布值全部转移到自己上来,这使得其他网页的概率分布值为0。
基于以上的考虑,有人指出,添加一个阻尼系数 d d d:
- 一方面为了这个阻尼系数用来表示一个概率,这个概率表示跳转到其他网页节点的概率,避免被自我引用导致其他都是0
- 另一种就是自己没有入链,这样最终自己的分数都是0,这样自己指向的网页最终也会为0,为了避免这种情况,会引入阻尼系数来给一个默认值
具体公式是:
P R ( p i ) = ( 1 − d ) + d ∗ ∑ p j ∈ E ( p i ) ( P R ( p j ) L e n ( p j ) ) PR(p_i) = (1-d)+d*\sum_{pj \in E(pi)}(\frac{PR(p_j)}{Len(pj)}) PR(pi)=(1−d)+d∗pj∈E(pi)∑(Len(pj)PR(pj))
d d d一般取0.85, ( 1 − d ) (1-d) (1−d)代表着不考虑入站链接的情况下随机进入一个页面的概率,也就是没有入链的情况下的节点权重。在0.85的阻尼系数下,大约100多次迭代就能收敛到PR向量。当阻尼系数接近1时,需要的迭代次数会陡然增加很多,且排序不稳定。
收敛问题
实际上,在随机过程理论中,上述矩阵被称为“转移概率矩阵”。这种离散状态按照离散时间的随机转移过程称为马氏链(马尔可夫链,Markov Chain),也就是我们把PageRank收敛性问题转化为了求马尔可夫链的平稳分布的问题,那么我们就可以从马氏链的角度来分析问题。因此,对于PageRank的收敛性问题的证明也就迎刃而解了,只需要证明马氏链在什么情况下才会出现平稳分布即可。我们可以知道马氏链有三个推论:
推论1. 有限状态的不可约非周期马尔可夫链必存在平稳分布。
推论2. 若不可约马尔可夫链的所有状态是非常返或零常返的,则不存在平稳分布。
推论3. 若{Xi}是不可约的非周期马氏链的平稳分布,则lim(n→∞)Pj(n) = Xi。
这一块恰好pagerank符合这三个推论,所以它是收敛的。
优点与缺点
点:评估网页排名其他因素考虑的更多一些,不仅仅是网页入链、出链。
优点:
- 优点:简单,容易实现
- PageRank算法通过网页间的链接来评价网页的重要性,在一定程度上避免和减少了人为因素对排序结果的影响;
- 采用与查询无关的离线计算方式,使其具有较高的响应速度 ;
- 一个网页只能通过别的网页对其引用来增加自身的PR值,且算法的均分策略使得一个网页的引用越多,被引用网页所获得的PR值就越少。
因此,算法可以有效避免那些为了提高网站的搜索排名而故意使用链接的行为。
缺点:
(1 )主题漂移问题
PageRank 算法仅利用网络的链接结构,无法判断网页内容上的相似性;且算法根据向外链接平均分配权值使得主题不相关的网页获得与主题相关的网页同样的重视度,出现主题漂移。
(2 )偏重旧网页问题
决定网页 P R 值的主要因素是指向它的链接个数的多少。一个含有重要价值的新网页,可能因为链接数目的限制很难出现在搜索结果的前面,而不能获得与实际价值相符的排名。 算法并不一定能反映网页的重要性,存在偏重旧网页现象。
(3 )忽视用户个性化问题
PageRank算法在设计之初,没有考虑用户的个性化需要。个性化搜索引擎的兴起,对 PageRank排序算法提出新的挑战。
参考博客
PageRank算法简介及Map-Reduce实现
PageRank算法的计算及其优缺点