《计算几何》01.Convex Hull
欢迎进入博客浏览
>>我的博客<<
更好的排版,更好的阅读体验
Convex Hull
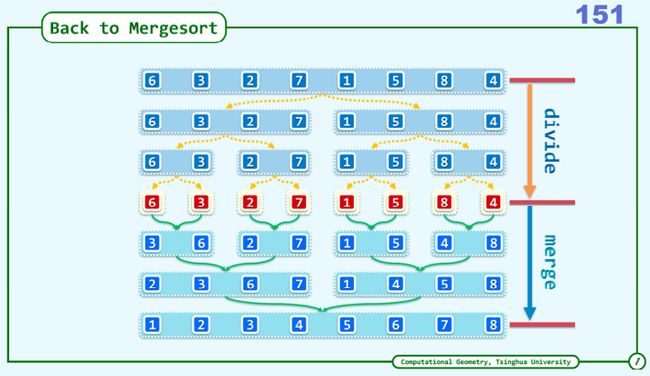
Divide-and-conquer
Merge
将大问题分解成小问题,最后进行合并。
Common Kernel
和归并排序一样,我们将点分成两个子集,分别求凸包,问题就变成了如何将两个凸包合并。
如何将两个凸包处理成星形多边形?
为了找到Star-shape-polygon,我们要找到两个多边形相交的公共的点,那么两个多边形相交会出现什么情况呢?
如上图所示,如 s 1 s_1 s1,是比较理想的情况,我们很容易找到公共点,对于 s 2 s_2 s2,找到公共点的可能就会小很多。
更坏的情况,例如 s 3 s_3 s3,我们甚至无法找到两个凸包的公共点,那么如何处理呢?
Interior
对于一个凸包来说,我们如何找到一个点使得这个点在凸包的内部呢?
我们可以选择凸包上任意三个点,选择这三个点组成的三角形的重心即可,计算复杂度为常数时间。
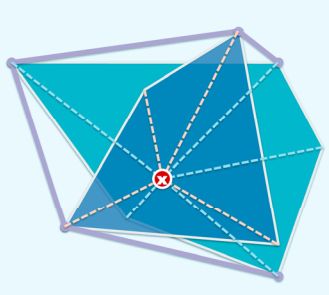
那么我们现在判断选出的内点是否在另一个凸包的内部,如果是:
可以发现两个凸包分别对于内点成一个环形的有序序列(图中黄色和蓝色的直线),则问题变成了经典的环形归并。归并之后再次进行Graham-Scan即可。
那么如何判断所选内点是否在另一个多边形内部呢?
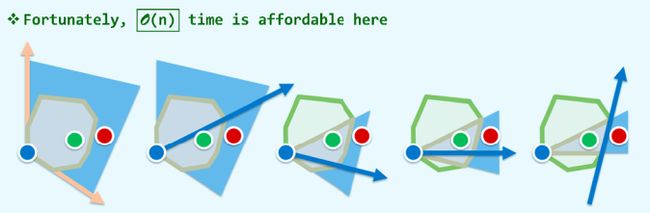
In-Convex-polygon-Test。但凸包是动态的,所以要用n次To-Left-Test:
幸运的是, O ( n ) O(n) O(n)次TLT并不会影响整体算法的复杂度,因为我们可以将这 n n n次操作都可以纳入Merge的过程中。
Exterior
接下来我们讨论下一种情况,所选内点落在另一个子凸包的外侧。
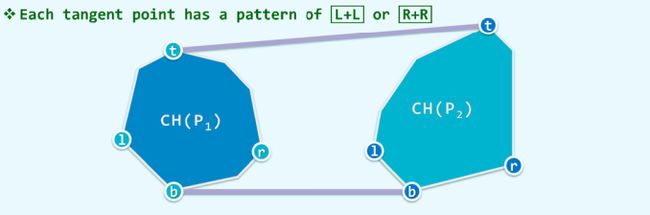
如图所示,我们可以找出图中 s , t s,t s,t 两个切点,找到 s t 和 t s st和ts st和ts 两个线段。同理, t s ts ts线段在总凸包中没有贡献。
那么我们可以得到了一个环形有序序列和一个线性有序序列,进行归并,再次Graham-Scan。
Divide-and-conquer (2)
Preprocessing
归并算法我们可以看到,有些过于复杂。对于两个图包:
如果他们沿着水平方向是可分割的,彼此独立,那么合并就非常的简单。
将点集中的坐标按x轴排序,取中点分割即可,那么我们关注的就是两个凸包中的两对点 l , r l,r l,r。
Common Tangents
找到两个凸包的公切线(Common Tangents)。那么如何找这两个凸包的公切线呢?问题可能很复杂:
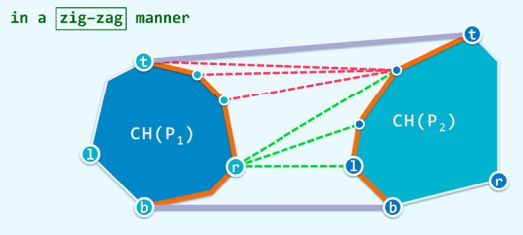
我们从 r r r和 l l l开始:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qGCTI8Y5-1584153950700)(C:\Users\szx74\Desktop\Blog\计算几何\image-20200314100712514.png)]
先将两个点连起来,那么恩么找到这两个点呢?我们在从最开始从下向上归并的过程中,记下每个凸包的 l , r l,r l,r即可。
接下来我们思考连接了 r , l r,l r,l之后的动作。
对于每次固定的 r r r,找到最优的右侧的 l l l,使得 l l l两侧的点都在它的同一侧,这样我们就得到了局部最优的 l l l,那么我们反观之前固定的 r r r,同样的方法找到局部最优的 r r r,再反观 l l l,反复进行,直到保证 r , l r,l r,l两个点都为最优,既两个点的临点皆再他们的同一侧,这样我们就找到了一条切线。时间复杂度为 O ( n + m ) O(n+m) O(n+m)。