【2020牛客多校九：树的BFS】K ：The Flee Plan of Groundhog

【传送门】K ：The Flee Plan of Groundhog

【难度】

$4/10$
认真想想也不会很难

【题意】

给定一棵树，$n$ 个节点 ，$n-1$ 条边
每条边权 为 1
小G一开始在 一 号节点。
小O一开始在 $n$ 号节点。
给定时间 $t$ 秒。

（1）
一开始，小G向小O移动 $t$ 秒，速度1/s，小O 则不动。
（2）
$t$ 秒后，小O 去追小G，小O的速度为2/s。
当然，此时小G会逃跑。
小G速度仍为1/s，但小G每回合可以移动或者不移动。
但是小O每回合必须移动。
（3）
每回合，先小G移动(或原地不动)，再小O移动。

求：小G在逃跑最优策略下，小O最少可以抓住小G的时间。

【数据范围】

$1\le n\le 10^5$
$1\le t\le n-1$
$1\le x,y\le n$

【输入样例】

$nt$
$x_1{y}_1$
$⋮$
$x_{n-1}{y}_{n-1}$

7 2
1 2
2 5
5 7
5 6
3 6
3 4

【输出样例】

1

【解释】

【思路】

首先，易得：

（0）考虑 $t$ 秒后，G在哪里

通过一次bfs，即可知道节点1 与节点n 之间的最短距离。
bfs时，记录每个节点的前驱结点即可知道 $t$ 秒后G的所处位置。

（1）考虑G的基本的逃跑最优策略

若G逃跑，一定是向根节点或者叶子节点（后面称为角落）跑是最优的。
最优不可能来回跑。
最优不可能还没跑到角落就等待。
若已经被抓到了(当前秒时两个人都在同一个节点)，则无法再逃跑。

（2）考虑G的逃跑方向

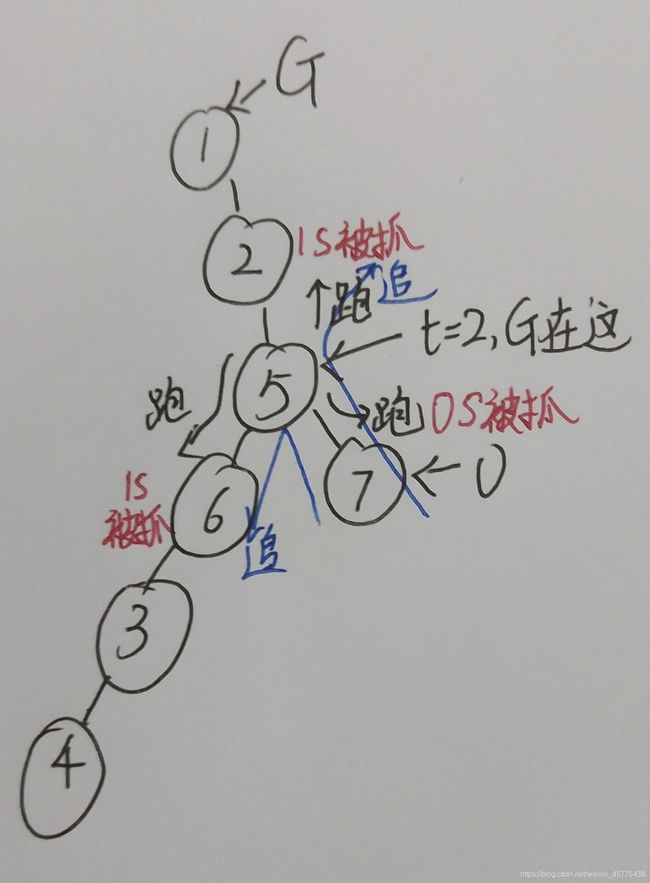
若 $t$ 秒后G的位置如图所示，他应该哪个方向逃跑？

若小O处在 $O2$ 位置，可以看出G应该往 $\alpha$方向逃跑
若小O处在 $O1$ 位置，可以看出G应该往 $\beta$方向逃跑
$\gamma$方向总是最劣的。

这样，可能因为小O的位置不同，答案就截然不同，那么我们考虑：

$dis2[i]$表示小G到节点 $i$ 的最短时间
$dis3[i]$表示小O到节点 $i$ 的最短时间

如果某个节点存在 G到达时O还没到达或者正好抓住他
则答案为：
$$ans=\underset{i}{\max }\{dis3[i],其中dis2[i]\le dis3[i]\}$$

【注意】

========================================

这里取的是 $dis3[i]$ 而不是 $dis2[i]$ （之前打错了！）
因为如果 $dis3[i]$ 大的话，表示跑到这个节点，小G就原地等待小O追上他了。
而取最大值是因为小G逃跑策略永远是最优的，所以取大值。

========================================
很可惜，这样是不大正确的，因为小O每秒可以跑两个单位。

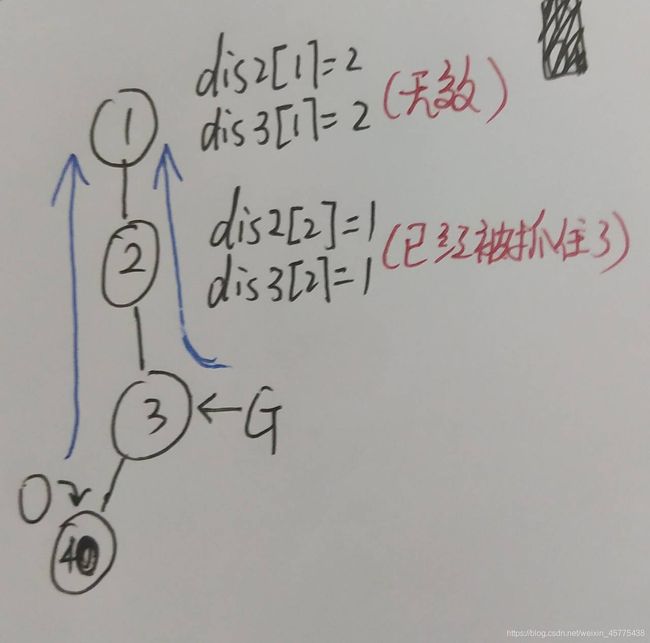
看图，可知对于节点1和2都成立，但是小G在节点2已经被抓到了，
他无法跑到节点1。

那么我们只要修改式子一下即可

$$\begin{gathered} ans=\underset{i}{\max }\{dis3[i],其中dis2[i]\le dis3[i],并且dis2[fa[i]]<dis3[fa[i]]\} \\ 其中fa[i]表示i的前驱结点 \end{gathered}$$

表示结点 i 正好O抓到了G，并且之前O还没抓到G。

【AC核心代码】

时间复杂度 $O(N)$

/*
 _            __   __          _          _
| |           \ \ / /         | |        (_)
| |__  _   _   \ V /__ _ _ __ | |     ___ _
| '_ \| | | |   \ // _` | '_ \| |    / _ \ |
| |_) | |_| |   | | (_| | | | | |___|  __/ |
|_.__/ \__, |   \_/\__,_|_| |_\_____/\___|_|
        __/ |
       |___/
*/
const int MAX = 1e5+50;

vector<int>G[MAX];
int dis[MAX];
int fa[MAX];
int n,t;

void bfs(){				/// 第一个bfs 计算t 时刻 G的位置等
    queue<int>Q;
    Q.push(1);
    dis[1] = 1;
    while(!Q.empty()){
        int x = Q.front();Q.pop();
        for(auto it : G[x]){
            if(!dis[it]){
                fa[it] = x;
                dis[it] = dis[x] + 1;
                Q.push(it);
            }
        }
    }
}
int dis2[MAX];
int dis3[MAX];
int yuan = 0;
void bfs2(int now){				///第二个bfs，计算dis2
    queue<int>Q;
    Q.push(now);
    dis2[now]=1;
    while(!Q.empty()){
        int x = Q.front();Q.pop();
        for(auto it : G[x]){
            if(!dis2[it]){
                dis2[it] = dis2[x] + 1;
                Q.push(it);
            }
        }
    }
}
int ans;
int fa2[MAX];
void bfs3(int now){    				///第三个bfs，计算dis3
    queue<int>Q;
    Q.push(now);
    dis3[now]=1;
    while(!Q.empty()){
        int x = Q.front();Q.pop();
        for(auto it : G[x]){
            if(!dis3[it]){
                fa2[it] = x;
                dis3[it] = dis3[x] + 1;
                Q.push(it);
            }
        }
    }
}
int main()
{
    scanf("%d%d",&n,&t);
    for(int i=1;i<n;++i){
        int ta,tb;
        scanf("%d%d",&ta,&tb);
        G[ta].push_back(tb);
        G[tb].push_back(ta);
        fa[i] = i;
    }
    bfs();
    int ci = dis[n] - t - 1;
    int now = n;
    for(int i=0;i<ci;++i){
        now = fa[now];
    }
    bfs2(now);
    bfs3(n);
    for(int i=1;i<=n;++i){			/// 见公式
        int zuo = dis2[i]-1;
        int you = (dis3[i]+1-1)/2;
        int zuo2 = dis2[fa2[i]] -1;
        int you2 = (dis3[fa2[i]]+1-1)/2;
        if(zuo<=you && zuo2<you2)ans = max(you,ans);
    }
    printf("%d",ans);
    return 0;
}