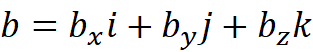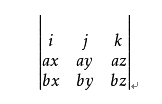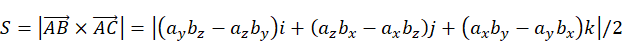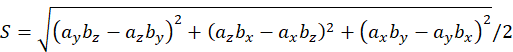向量积计算三角形面积
向量积:数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。
向量积可以被定义为:
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
![]()
向量积的模(长度)![]() 在数值上等于
在数值上等于![]() ,
,![]() ,及其夹角θ组成的平行四边形的面积。所以求三角形ABC的面积,根据向量积的意义,可得三角形ABC的面积S:
,及其夹角θ组成的平行四边形的面积。所以求三角形ABC的面积,根据向量积的意义,可得三角形ABC的面积S:
a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k,为了帮助记忆,利用三阶行列式,写成:
其中i,j,k是三个相互垂直的单位向量。它们刚好可以构成一个坐标系。
这三个向量的特例就是i=(1,0,0),j=(0,1,0),k=(0,0,1)。
即:
tips:空间向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是![]()
即:
因为是二维三角形,所以az,bz=0,所以:
![]()