C语言画分形之Julia集
最强大脑第四季有一位选手余彬晶挑战的就是“分形之美”,项目使用的是分形之Julia集,感兴趣的话可以看看 。下面进入正题:
分形
- 目前常用的造型技术
- 分形几何
- 背景
- 概念
- 对模型的基本要求
- 经典分形
- 利用graphic库画Julia分形
目前常用的造型技术
1.实体造型技术(Solid Modeling)
它将对象分解为一组有限的三维元素的集合以及可施加在这组集合元素上的一组操作,视这组三维元素(如体素、多边形等)及其操作的不同,实体造型技术还可以分为很多类型。
2.曲面造型技术(Surface Modeling)
它用数学函数(如B样条、贝塞尔、孔斯等函数)描述曲线和曲面,并提供曲面的修改、连接、求交和显示等操作。
3.非几何形体的造型技术
大多数自然物体,如山石、树木、花草、云霞、水波、火焰等都有不规则的非几何形状。非几何 形体的造型技术研究这类对象的表达与操作方法。典型的方法有:分数维(Fractal)方法、粒子系统(Particle System)等。它们都采用递归过程来产生数量很大的、表面看似乎是无规则的空间数据,并用参数控制其形状。
分形几何
背景
欧式几何的主要描述工具是直线,平滑的曲线,平面及边界整齐的平滑曲面,这些工具在描述一些抽象图形或人造物体的形态时非常有力,但对于一些复杂的自然景象形态就显的无能为力,诸如山,树,草,火,云,波浪等。这是由于从欧式几何来看,它们是极端无规则的。为了解决复杂图形生成问题,分形(Fractal)造型应运而生。
1904年,当时 Helge Von Koch 研究了一种他称为雪花的图形:科赫曲线(Koch curve)。将一个等边三角形的三条边都三等分,在中间的那 一段再凸起一个小三角形。这样一直下去,理论上可证明这种不断构造成的雪花周长是无穷的,但其面积却是有限的。这和正统的数学直观是不符的,周长和面积都无法刻画出这种雪花的特点,欧氏几何对这种雪花的描述无能为力。
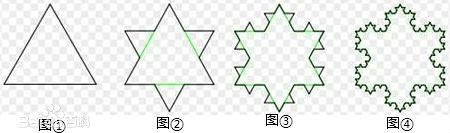
20世纪60年代开始,Benoit B. Mandelbrot 重新研究了这个问题,并将雪花与自然界的海岸线、山、树等自然景象联系起来【区别是雪花是理想的自相似图形,而自然界的其他物体并不一定是】,找出了其中的共性,提出了分形(Fractal)的概念。他提出了“英国的海岸线有多长?”的问题,以1km为单位测量海岸线,得到的近似长度将短于1km的迂回曲折都忽略掉了,若以1m为单位测量,则能测出被忽略掉的迂回曲折,长度将变大,测量单位进一步变小,测得的长度将愈来愈大,这些愈来愈大的长度将趋近于一个确定值,这个极限值就是海岸线的长度。海岸线的长度是不确定的,长度依赖于测量单位。
概念
Mandelbrot 注意到 Koch 雪花和海岸线的共同特点:它们都有细节的无穷回归,随着测量尺度的减少都会得到更多的细节。换句话说,就是将其中的一部分放大会得到与原来部分基本一 致的形态,这就是 Mandelbrot 发现的复杂现象的自相似性。为了定量地刻画这种自相似性,他引入了分形(Fractal)的概念。 但是需要指出的是分形并不一定是自相似。
这个概念强烈推荐观看3Blue1Brown的视频:https://www.bilibili.com/video/BV1wx411C7WT
里面有关于非整数维度及分形真正概念的形象分析。当你看到:分形就是有非整数维度的图形,;分形的概念不是为了美,而是为了实用;分形几何是对微积分的反抗,微积分的核心假设是物体放大之后会变得更加光滑,而分形是考虑放大之后仍然粗糙…一定会有更多的收获!!
设N为每一步细分的数目,S为细分时的放大(缩小)倍数,则分数维D的定义为D=(log N)/log(1/S)【维度不一定是整数】
以Koch 雪花为例,它的每一步细分线段的个数为4,而细分时的放大倍数为1/3(一条边是原来所在边的1/3),则雪花边线的分数维D=1.2619。如果按欧氏几何的方法,将一线段四等分,则N=4,S=1/4,D=1。如将一正方形16等分,此时N=16,线段的放大倍数 S=1/4,则D=2。
对模型的基本要求
(1)能逼真地“再现”自然景象。所谓逼真是指从视觉效果上逼真,“再现”即不要求完全一致;
(2)模型不依赖于观察距离,即距离远时可给出大致轮廓和一般细节,距离近时能给出更丰富的细节;
(3)模型说明应尽量简单,模型应具有数据放大能力;
(4)模型应便于交互地修改;
(5)图形生成的效率要高;
(6)模型适用范围尽可能地宽。
经典分形
(1)Koch曲线
(2)Cantor集
(3)Sierpinski垫片
(4)Sierpinski海绵
(5)Julia集
(6)Mandelbrot集
利用graphic库画Julia分形
1.含义:
在复平面上,水平的轴线代表实数,垂直的轴线代表虚数。每个Julia集合(有无限多个点)都决定一个常数C,它是一个复数。在复平面上任意取一个点,其值是复数Z。将其代入下面方程中进行反复迭代运算: Z n + 1 Z_{n+1} Zn+1= Z n 2 Z_n^2 Zn2+C 其中 C=p+qi
如:

迭代函数:f(z)= z 2 z^2 z2+(0.33+0.4i)
2.Julia集的生成过程
(1)选定屏幕分辨率为a*b,可显示的颜色为K+1种,分别以数字0,1,2,…,K表示; Z i Z_i Zi= x i x_i xi+ y i y_i yii,从 Z i Z_i Zi到 Z i + 1 Z_{i+1} Zi+1的迭代过程就是
x i + 1 x_{i+1} xi+1 = x i 2 x_i^2 xi2- y i 2 y_i^2 yi2+p;
y i + 1 y_{i+1} yi+1 =2 x i x_i xi y i y_i yi+q;
(2) 确定复平面的坐标范围,设选定参数x_min=y_min=-1.5,x_max=y_max=1.5,又取M=100;
令 △x=(x_max-x_min)/(a-1)
△y=(y_max-y_min)/(b-1)
对所有的视区的点(nx,ny),nx=0,1, …,a-1及ny=0,1,…,b-1完成下面的循环;
(3)令x0=x_min+nx* △x,y0=y_min+ny* △y,k=0;
(4)由迭代过程从(xi,yi)算出( x i + 1 x_{i+1} xi+1, y i + 1 y_{i+1} yi+1),并计算k:=k+1 (5) 对点(nx,ny)显示颜色k并转至下一点,再从头作步骤(3)。
计算r= x i 2 x_i^2 xi2+ y i 2 y_i^2 yi2。
如果r>M,则选择颜色k,转至步骤(5);
如果k=K,则选择颜色0,转至步骤(5);
如果r≤M,且k#include
