分形造型的常用模型，C构造简单的IFS图形

随机插值模型

该模型是1982年由Alain Fournier, DonFussell和Loren Carpenter提出的，它能有效地模拟海岸线和山等自然景象。
为了克服传统模型技术中依赖观察距离的局限性，随机插值模型不是事先决定各种图素和尺度，而是用一个随机过程的采样路径作为构造模型的手段。例如，构造二维海岸线的模型可以

• 选择控制大致形状的若干初始点；
• 在相邻两点构成的线段上取其中点，并沿垂直连线方向随机偏移一个距离；
• 再将偏移后的点与该线段两端点分别连成两条线段。

这样下去可得到一条曲折的有无穷细节回归的海岸线，其曲折程度由随机偏移量控制。它也决定了分数维的大小：
图一

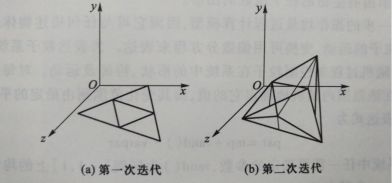
在三维情况下可通过类似过程构造山的模型，一般通过多边形（简单的如三角形）细分的方法。可以在一个三角形的3条边上随机各取一点，并沿垂直方向偏移一定距离后得到新的3个点，再连接成4个三角形，如此继续，即可形成褶皱的山峰。山的褶皱程度由分数维控制：
图二

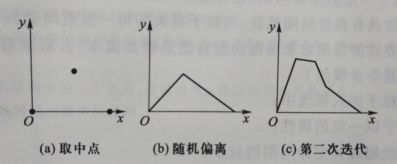
下面以画出Sierpinski三角形举例

步骤
a.给三角形的3个顶点，和一个当前点；
b.随机选择三角形的某一个顶点，计算出它与当前点的中点位置；
c.将计算出的中点做为当前点，再重新执行操作a。

#include
#include
#include 
#include

#define PI 3.14159265

int max_iter=10000;//迭代次数 

double point[3][2]={
	0,100*tan(PI/3),
	100,0,
	200,100*tan(PI/3)
};//三角形三个顶点坐标 
      
void Sierpinski(double x0,double y0,int k){
	if(k>max_iter) return;
	int rnum=rand()%3;//设置概率 
	if(rnum==0){
		x0=(x0+point[0][0])*0.5;
		y0=(y0+point[0][1])*0.5;
	}
	else if(rnum==1){
		x0=(x0+point[1][0])*0.5;
		y0=(y0+point[1][1])*0.5;
	}	
	else{
		x0=(x0+point[2][0])*0.5;
		y0=(y0+point[2][1])*0.5;
	}
	k++;
	putpixel(x0,y0,YELLOW);
	Sierpinski(x0,y0,k);
}
int main(){
	initgraph(1000,1000);
    double x0=100,y0=0;//给一个当前点 x0,y0	
 	Sierpinski(x0,y0,0);
	getch();
	closegraph();
	return 0;
} 

运行：

迭代函数系统（IFS）

概念：
迭代函数系统是从一个坐标系到另一个坐标系的映射系统。迭代函数系统是以下述方式工作的：取空间中任一点$Z_0$，以$P_i$ 概率选取变换$M_i$，作变换$Z_i$=$M_i$($Z_0$)，再以$P_i$的概率选取变换$M_i$，对$Z_1$做变换$Z_2$＝$M_i$($Z_1$)，以此下去，得到一个无数点集。

IFS 的压缩映射 $w_i$ 的参数设计 ：
由分形图的相似结构, 每一个压缩映射 $w_i$是 由平移、 旋转和比例 3 种变换以及它们的复合变换构成的仿射变换， 二维形式为 :

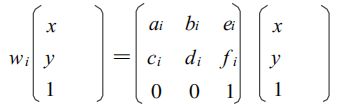
三种变换是：

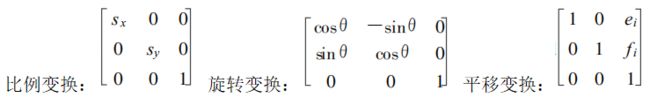
其中参数 $a_i$ , $b_i$ , $c_i$ , $d_i$ 由旋转 、 比例变换所决定的实数 ;$e_i$, $f_i$ 由平移变换所决定的实数 。三维形是由相应的三维空间几何变换复合而成。

IFS 吸引子自然景观的模拟总是在一个矩形区域内进行 , 取度量空间 ([ 0 , 1] × [ 0 , 1] , d), 由于$w_i$ 是压缩变换, $w_i$ ([ 0 , 1] × [ 0 , 1] ) [ 0 , 1] × [ 0 , 1] 。因此, 参数 $a_i$ , $b_i$ , $c_i$ , $e_i$, $f_i$的取值范围在 [ -1 , 1] ;$e_i$ 的取值影响植物x 方向的偏离程度,$f_i$,的取值影响植物在竖直y方向的生长程度 , 一般取值为正。

IFS 中概率 p1 , … , pn 的参数设计:
p1 , p2 , …, pn 的大小分配并不影响最终吸引子, 也就是绘制的图形完全由 $w_i$ (i =1 , 2 , …, n)确 定 , 与 p1 , p2 , … , pn 无关 , p1 , p2 , …, pn 只是为计算机编程绘图提供了极大的方便 , p1 , p2 , …, pn 的大小分配只影响绘图的速度, 即迭代次数。

IFSP码举例：
Sierpinski 三角形的IFS代码:

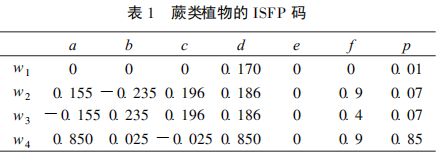
w	a	b	c	d	e	f	p
1	0.5	0	0	0.5	0	0	0.33
2	0.5	0	0	0.5	0.5	0	0.33
3	0.5	0	0	0.5	0.25	0.5	0.34

《分形图的 IFS 码设计》这篇文章中包含IFS 参数设计的详细介绍，可参阅【直接下载】
https://download.csdn.net/download/qq_43606914/12446875

下面使用IFS画出蕨类植物

#include
#include
#include
int Iter=10000;

double a[4][7]={
		0, 0, 0, 0.170, 0, 0, 0.01 ,
		0.155,-0.235,0.196,0.186,0,0.9,0.07,
		-0.155,0.235,0.196,0.186,0,0.4,0.07,
		0.850,0.025,-0.025,0.850,0,0.9,0.85
};

void IFS_Tree(double x0,double y0,int k){
	if(k>Iter) return;
	int tmp=rand()%100;
	if(tmp<=1){
		x0=a[0][0]*x0+a[0][1]*y0+a[0][4];
		y0=a[0][2]*x0+a[0][3]*y0+a[0][5];
	}
	else if(tmp<=8){
		x0=a[1][0]*x0+a[1][1]*y0+a[1][4];
		y0=a[1][2]*x0+a[1][3]*y0+a[1][5];
	
	}	
	else if(tmp<=15){
		x0=a[2][0]*x0+a[2][1]*y0+a[2][4];
		y0=a[2][2]*x0+a[2][3]*y0+a[2][5];
	}
	else{
		x0=a[3][0]*x0+a[3][1]*y0+a[3][4];
		y0=a[3][2]*x0+a[3][3]*y0+a[3][5];
	}
	putpixel(x0*100+300,600-y0*100,WHITE);
	k++;
	IFS_Tree(x0,y0,k);
}
int main(){
	initgraph(1000,1000);
	srand((unsigned)time(NULL));
    double x0,y0=0;	
	x0 = rand()%200+1;
	y0 = rand()%200+1;
    IFS_Tree(x0,y0,0);
	getch();
	closegraph();
	return 0;
} 

运行：

L系统

L系统（short for Lindenmayer systems）是比较新的制作分形的方法。这项技术是Aristrid Lindenmayer在1968提出来的，最早是用来研究植物生长的生物模型。原理即是用字符串来描述一棵树，一朵花，甚至雪花等等。

L-system 包含三个部分：

1. Alphabet： L系统的字母由可以包含的有效字符组成。例如，字母是“
   ABC”，那么L系统中的任何有效字符串只能包含这三个字符。
2. Axiom：描述系统初始状态的句子（由字母中的字符组成）。
3. Rule： L系统的规则被应用于Axiom，然后被递归地应用，一遍又一遍地产生新的句子。L系统规则包含两个句子。例如，使用规则“ A —> AB”，只要在字符串中找到“ A”，就会将其替换为“ AB”。

L系统通常使用以下字母：“ FG ±[]”，表示：
F：画一条线并向前移动
G：前进（不画线）
+：右转
-：左转
[：保存当前位置
]：恢复上一个位置