数字滤波器设计(IIR与FIR)(持续更新)
文章目录
- 1. 信号处理方面整理
- 1 滤波器
- 2 线性相位,全通滤波器,群延迟
- 3 截止频率与时间的关系
- 2 [奥本海默信号处理课程](https://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/lecture-notes/);
- 实数信号频谱的对称性,复数信号的采样
- 滤波器的部分
- 信号处理工具
- 如何利用fdatool设计滤波器?
- 如何理解窗函数与设计窗函数?
- 3 如何设计滤波器
- FIR与IIR
- 定义
- 性能
- 延时
- 设计
- 抗混叠滤波器
- 吉布斯现象
- 采样定理
- 泄漏
1. 信号处理方面整理
1 滤波器
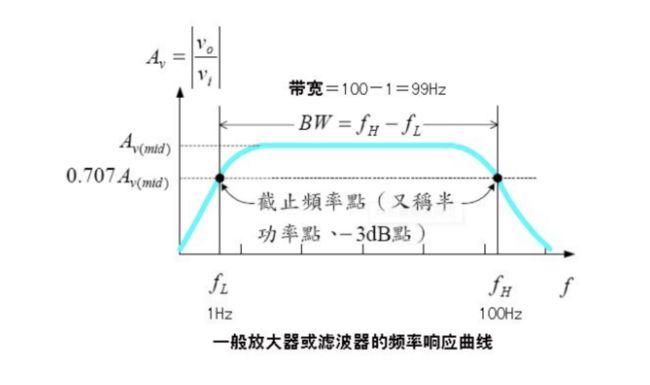
滤波器的截止频率:
无论是什么样的滤波器,一般都是指-3db的位置,也就抄是说从滤波器的通带的增益算起,下降-3db的位置。由于db的计算公式是20*log10(x),x为信号某一个频率上真正的幅值,所以稍加计算可得,-3db实际相当于频率增益下降到了原来的0.707,而不是一半。这里解释了什么是截止频率?
对于低通滤波知器,是低于某个频率为通带,高于某个频率为阻带。如果要输入道9.5KHz~1.5KHz的方波,则9.5KHz~1.5KHz这些频率必须在通带之内,所以滤波器的截止频率要高于9.5KHz。
当某人问你一个FIR滤波器的脉冲响应时,他等于是在问你FIR滤波器的系数。
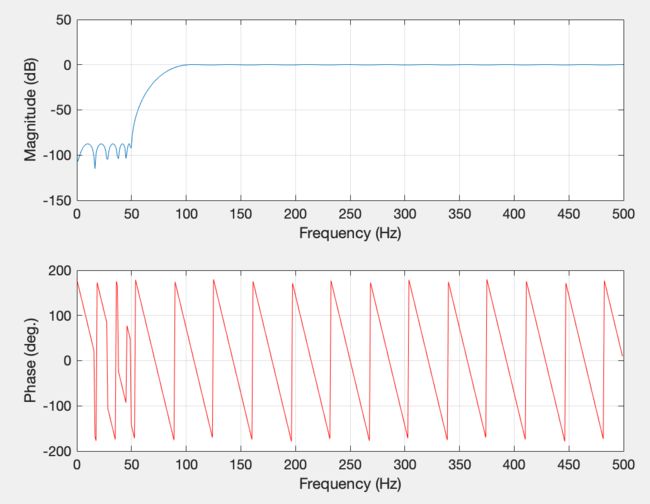
如上图所示,可以观察到输出信号和输入信号频率相同,这是LTI系统的本质,输入某个频率的正弦信号,输出同样是该频率的正弦信号,只不过幅度和相位发生了改变。
其次,可以注意到输出信号的前面4个点不是正弦形状的,这些点只是滤波器的暂态过渡响应。在这种抽头延迟线FIR滤波器中,过渡响应点数与滤波器的延拓单元数量D相同,在过渡响应之后才是滤波器的稳态时域响应。它意味着对于拥有D个延迟器的抽头延迟线FIR滤波器而言,前面D个系统的输出并不能代表系对该序列的正确响应。直到D+1个输出才是系统对该序列的准确响应。
G(jω)=A(ω) expΦ(ω)(频率响应)
G(jω)称为频率特性,A(ω)是输出信号的幅值与输入信号幅值之比,称为幅频特性。Φ(ω)是输出信号的相角与输入信号的相角之差,称为相频特性。
那么也就是说不同频率的信号得到的相位差还不一样?这是和什么相关?
相位差如下:
dt = 1/fs;
dt/T = 0.8*pi(相位响应)/2*pi
使用的滤波器如下:(这是不是就是线形相位呢?)
2 线性相位,全通滤波器,群延迟
1 线形相位
num 是传递函数的分子,den是传递函数的分母。分母只有 a0 = 1, 代表是一个FIR滤波器。分子b0 = 0, b1 = 1, 代表是一个采样点的延迟。
2 全通滤波器
设计一个全通滤波器:
相频曲线如下图所示:
举例来说:就音乐厅来说,如果把舞台上音乐家的歌唱声或乐器发出的声音作为输入,听众听到的上述声音作为输出的话,那么音乐厅可以看成输入输出之间的一个系统。最理想的情况是,输出与输入之间只有一个类似于延时的线性相位滤波器,也即是舞台上唱什么歌,听众就能听到什么歌,只是时间上稍微有滞后。
如果音乐厅这个系统不是线性相位的,会出现什么情况呢?音乐是由很多不同的频率成分构成的。这时候音乐中有些频率成分很快就从舞台上传过来了,有些频率成分则要过一阵才传过来。这样组合起来的音乐,先不论是否悦耳,至少和舞台上的已经不一样了。这时候也就意味着坐在不同位置的听众,听到的将是不同的音乐。这是人们不希望看到的。
这种情况下,必须要求线性相位的响应。该举例转载于博客《线性相位重要性的理解》。下面这篇博客介绍了线性滤波器在ECG信号中的使用,也是通俗易懂,可以参考。《为什么设计的滤波器一定要用线性相位》
3 截止频率与时间的关系
参考;
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rwhBJtAb-1596440997846)(/Users/chenshiming/Library/Application%20Support/typora-user-images/image-20200523151754825.png)]
这里将阶跃响应作为输入,得到输出。为什么?为什么是阶跃响应呢?因为求取微分方程组就是需要阶跃响应。同时阶跃响应代表了系统的性质。
2 奥本海默信号处理课程;
两个时间域上卷积的傅立叶变换是两个傅立叶变换的乘积。也就是说在LTI的滤波器中我在时间域上的输出,就是输入与系统脉冲响应的卷积。基本上,在频率域输出的傅立叶变换是脉冲响应的傅立叶变换, 也就是频率响应和输入的傅立叶变换的乘积。
为什么脉冲响应就是频率响应?
一个是时域上,一个是频域上,有什么区别呢?
频率响应不是对应的是频域上的不同w的响应吗?如何对应到时域上。
在DRcan的视频中,一个很重要的内容是“频率响应”。
阶跃响应与脉冲响应的区别?利用系统的阶跃响应可以探测系统的性质。
实数信号频谱的对称性,复数信号的采样
滤波器的部分
如果频率域上是实数的话,那么时域上就是一个偶函数。
信号处理工具
如何利用fdatool设计滤波器?
可以看到两个相位图不一样,为什么?
如何理解窗函数与设计窗函数?
参考Understanding FFTs and Windowing
https://www.jianshu.com/p/67199ba545ef
3 如何设计滤波器
FIR与IIR
FIR与IIR,这个博客值得一看。
抗混叠滤波器–抗混叠滤波器用于删除在模数转换之前无法正确数字化的信号内容。
定义
“脉冲响应”是指滤波器在时域中的外观。滤波器通常具有较宽的频率响应,对应于时域中的短持续时间脉冲,如图6所示。
性能
IIR和FIR实现之间的数学差异是IIR滤波器使用一些滤波器输出作为输入。这使IIR滤波器具有“递归”功能。
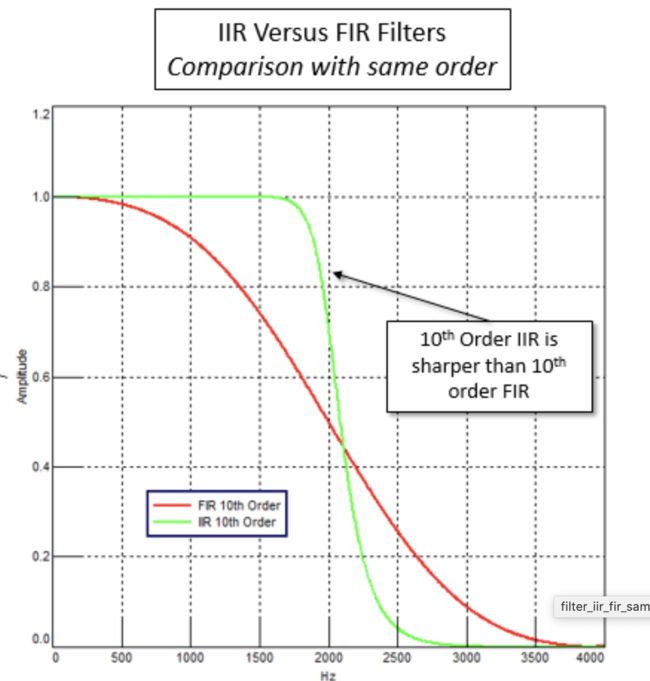
对于如图11所示的相同顺序,FIR和IIR滤波器的清晰度非常不同。由于IIR滤波器的递归性质(请参见公式1),其中部分滤波器输出用作输入,因此使用相同阶数的滤波器可以实现更清晰的滚降。
但是,使用IIR滤波器存在一些潜在的缺点:
- 延迟-IIR滤波器在不同频率下具有不相等的延迟,而FIR在每个频率下具有一致的延迟。
- 稳定性–由于其结构,IIR滤波器有时可能不稳定,无法计算或应用于数据。FIR滤波器的配方始终稳定。
延时
FIR滤波器在所有频率上具有相同的时间延迟,而IIR滤波器在每个频率上具有可变的时间延迟。通常,IIR滤波器中最大的时间延迟是滤波器的截止频率。
零相位滤波器:是为了解决信号的相位延时的问题。
设计
FIR滤波器方法*
下面列出了有限冲激响应(FIR)滤波器的方法,如图18所示*:*
从频域转换到时域时,FIR方法使用不同的频谱窗口。一些窗口方法包括:
- 切比雪夫–阻带中的纹波量最少,但过渡带最宽。
- 汉明–过渡区较窄,波纹小于汉宁。由曼哈顿项目的成员Richard Hamming开发。
- 凯撒(Kaiser)–由贝尔实验室的詹姆斯·凯撒(James Kaiser)开发,凯撒(Kaiser)窗口在停止区具有较小的振幅波动,只有宽的过渡宽度切比雪夫(Chebyshev)具有较低的振幅波动。
- 汉宁–最窄的过渡带,但阻带中的波纹很大。
- 矩形–最大的波纹/波瓣,甚至会影响通带。
6.2 IIR方法
无限脉冲响应滤波器的方法如图19所示*:*
不同的IIR滤波器方法的属性:
- 巴特沃思–在通带和阻带中响应平坦,但过渡区域较宽。1930年由英国物理学家斯蒂芬·巴特沃思(Stephen Butterworth)首次描述。
- 切比雪夫逆滤波器–通带内平坦,过渡宽度比巴特沃斯滤波器更窄,但阻带内有纹波。如果阻带中的纹波不是问题,则对于给定的应用,它可能比Butterworth滤波器更可取。
- 切比雪夫–可以在通带中产生纹波,但是比逆切比雪夫具有更陡峭的滚降。
- Cauer –最窄的过渡带。阻带和通带中的波纹。有时称为椭圆滤波器。
- 贝塞尔(Bessel)–通带和阻带中都有倾斜的幅度,过渡区域非常宽。滤波器中的延迟与频率关系在此列表中最平坦。贝塞尔滤波器以德国数学家弗雷德里希·贝塞尔(1784-1846)的名字命名。
抗混叠滤波器
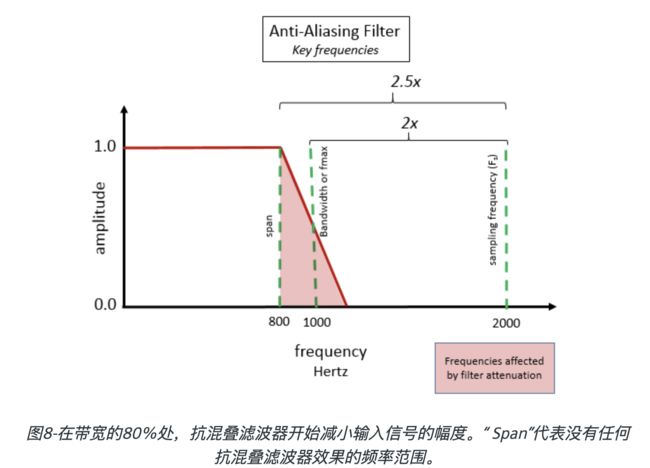
混叠可能导致频谱内容被镜像到带宽附近,从而导致频率内容的错误表示。为了防止这种情况,实施了抗混叠滤波器。带宽的无混叠部分称为跨度。跨度是带宽的前80%。请记住,请始终将带宽设置为比所需的最高频率高20%,以避免出现混叠。
吉布斯现象
用来描述时域上的影响。
吉布斯现象对测得的时间信号的影响可以大大减少或消除。请记住以下几点:
- 吉布斯现象会产生带有不可预测的过冲的振铃信号,可以通过在数据采集期间正确使用抗混叠低通滤波器来控制吉布斯现象。滤波器的频率截断和滤波器的形状都会影响吉布斯现象的幅度和持续时间。
- 吉布斯现象在包含阶跃或不连续性的瞬态信号中可以观察到。该现象不会在正弦信号上发生。它仅在数据采集过程中信号的一部分频率内容被删除时才会发生。
- 吉布斯现象的主要影响是在时域,而不是频域。
带宽(F max)是可以分析的最大频率。带宽是采样频率的一半(图7)。奈奎斯特采样标准要求将采样率至少设置为最大感兴趣频率的两倍。
1000赫兹的带宽意味着采样频率设置为2000样本/秒。
实际上,即使采样率为2000 Hz,实际可用带宽也可能小于理论极限1000赫兹。这是因为在许多数据采集系统中,都有一个抗混叠滤波器,它开始从80%的带宽开始减小信号的幅度。
采样定理
对于1000赫兹的带宽,抗混叠滤波器将带宽减小到800赫兹及以下。在这种情况下,滤波器会衰减800赫兹以上的频率。
简单认为是数据的长度,实际上就是分析这段数据的长度。
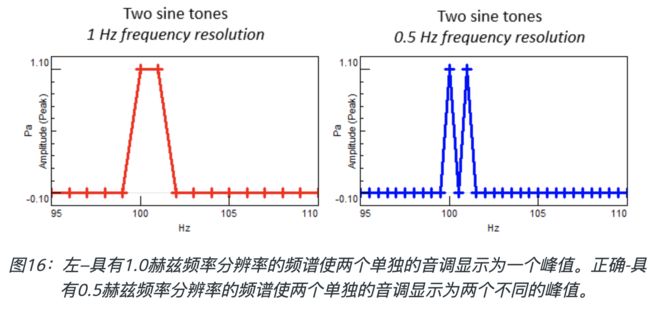
这个参数决定了delta_f,也就是傅立叶变换之后的分辨率。
在0.5赫兹(而不是1.0赫兹)的更高频率分辨率下,频谱显示了两个单独且不同的峰。更好的频率分辨率的好处非常明显。这可能是个问题,为什么不在所有情况下都使用最好的频率分辨率?
需要权衡。根据“黄金方程式”,每帧的时间数据量越高,因为频率分辨率越精细*(图13)*。这可能需要长时间的数据采集:
- 需要10 Hz的频率分辨率,仅需要0.1秒的数据
- 1赫兹的频率分辨率需要1秒钟的数据
- 0.1赫兹的频率分辨率需要10秒的数据
- 0.01赫兹的频率分辨率需要100秒的数据!
泄漏
什么是泄漏?如何避免泄漏?
韩宁窗:
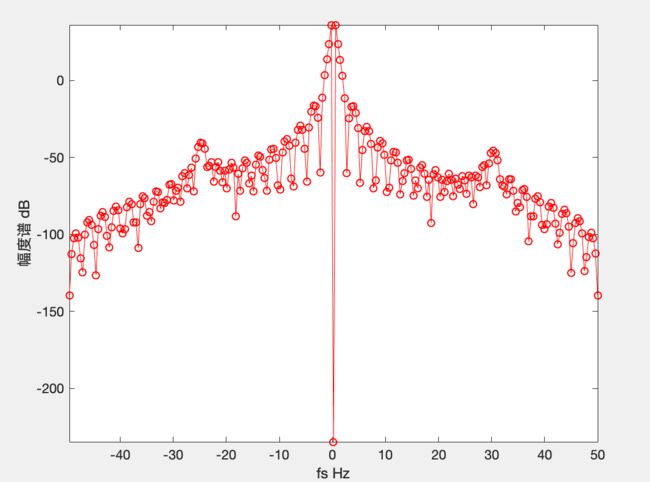
实例:
信号有两个频率:-25Hz与30Hz,但是由于delta_f太小,无法准确识别频率。
加上韩宁窗之后:
sig = conv(hanning(200),sig);