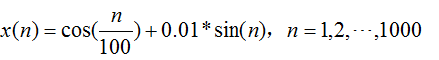IIR和FIR滤波器设计低通滤波器

设原始信号为

采用IIR滤波器和FIR滤波器设计低通滤波器，比较两类滤波器的滤波结果。

要求：采用MATLAB语言实现，并分析结果。

• 设计过程

首先对原始信号进行频谱分析，确定滤波器参数。通过分析加噪信号的频谱，噪声信号为，

原始信号为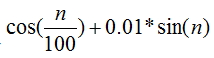。所以确定参数ωp=0.1π，ωs=0.25π；αp=0.08，αs=8；采样间隔T=8s。

1. IIR滤波器设计

按照数字滤波器技术指标（通带边界频率Wp 通带最大衰减 阻带截止频率 阻带最小衰减）要求设计一个过渡模拟低通滤波器Ha(s)，再使用脉冲响应不变法或双线性变换法将Ha(s)转换成数字低通滤波器的系统函数H(z)。本题采用双线性变换法，具体转换关系为：

 

由参数设计巴特沃斯滤波器，根据[N,wc]=buttord(wp,ws,Rp,As,’s’)计算模拟滤波器的阶数及截止频率，由[B,A]=butter(N,wc,Rp,’s’)计算模拟滤波器系统函数的分子和分母多项式的系数向量B和A。

1. FIR滤波器设计

（1）根据对阻带衰减及过渡带的指标要求，选择窗函数的类型，并估计窗口的长度N。

（2）构造希望逼近的频率响应函数Hd（e^jw）

（3）计算hd(n)

（4）加窗得到设计结果：h（n）=hd(n)*w（n）

采用[n,Wn,beta,type]=kaiserord(f,a,dev)函数来估计滤波器的阶数，根据阻带衰减及过渡带的指标要求，选择窗函数的类型（本题使用方法二及凯塞窗滤波器） 。这里f对应的频率，a=[1,0]为f指定的各个频带上的幅值向量，一般只有0和1表示。Devs用于指定各个频带输出滤波器的频率响应与其期望幅值之间的最大输出误差或者偏差。

 

 

 

 

 

 

结果分析：

A.相同技术指标下滤波器阶数

IIR滤波器阶数：6；

FIR滤波器阶数：14。

由此可以得到，为了达到相同的技术指标，即通带截止频率、阻带起始频率、通带内衰减、阻带内衰减，FIR滤波器所需的阶数更高,因为FIR滤波器传输函数的极点固定在原点，所以只能用较高的阶数达到高的选择性；对于同样的滤波器设计指标，FIR滤波器所要求的阶数可以比IIR滤波器高5~10倍，结果，成本较高，信号延时也较大；如果按相同的选择性和相同的线性要求来说，则IIR滤波器就必须加全通网络进行相位较正，同样要大增加滤波器的节数和复杂性。

B.滤波后信号频谱图的分析

由图6，FIR滤波器主要采用非递归结构，不论在理论上还是在实际的有限精度运算中都不存在稳定性问题，运算误差也较小。此外，FIR滤波器可以采用快速付里叶变换算法，在相同阶数的条件下，运算速度可以快得多。可以看出，经两种滤波器滤波后输出的信号频谱，FIR滤波后信号的频谱更接近实际无噪声信号的频谱。

 

• 程序

clear;

close all;

clc

 

n=1:8:8000;%以8为间隔取1000个点

s(n)=cos(n/100);%噪声信号

x(n)=cos(n/100)+0.01*sin(n);%原始信号

n1=1:512;%对采样后序列进行512点傅里叶变换

fk=1:8000/512:8000;%横坐标转化为频率

%无噪信号和原始信号

figure(1)

subplot(1,2,1)

plot(n,s(n))

xlabel('n');

ylabel('s(n)');

title('无噪信号');

hold on

subplot(1,2,2)

plot(n,x(n))

xlabel('n');

ylabel('x(n)');

title('原始信号');

fw=fft(s(n),512);

fw1=fft(x(n),512);

mag=abs(fw);

mag1=abs(fw1);

%原始信号频谱分析

figure(2)

subplot(1,2,1)

plot(fk/8000,20*log10(mag),'b')

xlabel('w');

ylabel('幅度');

title('无噪信号频谱');

hold on

subplot(1,2,2)

plot(fk/8000,20*log10(mag1),'r')

xlabel('w');

ylabel('幅度');

title('原始信号频谱');

%IIR滤波器设计

wp=0.1*pi;%通带截止频率

ws=0.25*pi; %阻带起始频率

Ap=1; %通带内衰减

As=8; %阻带衰减

T=1;   

WP=(2/T)*tan(wp/2);

WS=(2/T)*tan(ws/2);  

[N,Wc]= buttord(WP,WS,Ap,As,'s');%返回滤波器阶数和3dB截止频率    

[bt,at]=butter(N,Wc,'s');%计算低通滤波器系统函数H(s)

[bd,ad ]=bilinear(bt,at,1/T);   %用双线性变换法设计数字滤波器，数字滤波器的频率响应

[hd,wd]=freqz(bd,ad,512);   %画图

fw2=fft(hd,512);

mag2=abs(fw2);

figure

plot(fk/8000,20*log10(mag2),'r')

hold on

plot(fk/8000,20*log10(mag1),'b')

title('原始信号频谱和IIR滤波器频谱对比图');

legend('IIR滤波器频谱','原始信号频谱')

y=filter(bd,ad,x(1));

%%FIR滤波器的设计

fcuts = [0.1  0.25]; %归一化频率omega/pi，这里指通带截止频率、阻带起始频率

mags = [1 0];

devs = [10^(-Ap/20) (10^(As/20)-1)/(10^(As/20+1))];

[nn,Wn,beta,ftype] = kaiserord(fcuts,mags,devs);  %计算出凯塞窗N，beta的值

hh=kaiser(nn+1,beta);

fw2=fft(hh,512);

mag22=abs(fw2);

figure

plot(fk/8000,20*log10(mag1),'r')

hold on

plot(fk/8000,20*log10(mag22),'b')

xlabel('w');

ylabel('幅度');

title('原始信号频谱和FIR滤波器频谱对比图');

legend('原始信号频谱','FIR滤波器频谱');

%去噪效果对比

figure

y1=filter(hh,5,x(n));

plot(y1,'g')

hold on

plot(y,'r')

hold on

plot(s(n),'b')

title('原始信号频谱和滤波器频谱对比图');

legend('FIR','IIR','无噪信号')

figure

fwww=fft(y,512);

magnewiir=abs(fwww);

plot(fk/4000,20*log(magnewiir),'r')

hold on

fwwww=fft(y1,512);

magnewfir=abs(fwwww);

plot(fk/4000,magnewfir,'b')

hold on

plot(fk/4000,20*log(mag1),'k')

legend('iir滤波后频谱','fir滤波后频谱','原始有噪声信号频谱');