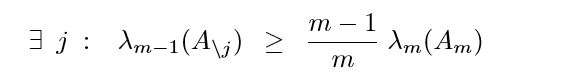Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]
文章目录
- 概括
- Sparse PCA Formulation
- 非常普遍的问题
- Optimality Conditions
- 条件1
- 条件2
- Eigenvalue Bounds
- 分隔定理的证明(《代数特征值问题》p98)
- 另外一个性质
- 算法
- 代码
![Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]_第1张图片](http://img.e-com-net.com/image/info8/dfdd3b6bf7de464caf535921a280c0f1.jpg)
概括
这篇论文,不像以往的那些论文,构造优化问题,然后再求解这个问题(一般都是凸化)。而是,直接选择某些特征,自然,不是瞎选的,论文给了一些理论支撑。但是,说实话,对于这个算法,我不敢苟同,我觉得好麻烦的。
Sparse PCA Formulation
非常普遍的问题
Optimality Conditions
这一小节,论文给出了,上述问题在取得最优的情况下应该符合条件。
条件1
如果 x ∗ C a r d ( x ∗ ) = k x^{*} \quad \mathbf{Card}(x^{*})=k x∗Card(x∗)=k是上述问题的最优解,那么 z ∗ z^{*} z∗(由 x ∗ x^{*} x∗非零元组成)是子举证 A k ∗ A_k^{*} Ak∗( x ∗ x^{*} x∗非零元所在位置, A A A的 k k k行 k k k列)的主特征向量。
这个条件是显然的。
条件2
Eigenvalue Bounds
这个定理,可以由一个事实导出:
A ∈ R n × n A \in \mathbb{R}^{n\times n} A∈Rn×n为一对称矩阵, λ i \lambda_i λi为其特征值,且降序排列。
A n − 1 A_{n-1} An−1为 A A A的任意 n − 1 n-1 n−1级主子式, δ i i = 1 , 2 , … , n − 1 \delta_i \quad i=1,2,\ldots,n-1 δii=1,2,…,n−1为其特征值,那么有下面分隔:
λ 1 ≤ δ 1 ≤ λ 2 ≤ … ≤ δ n − 1 ≤ λ n \lambda_1 \leq \delta_1 \leq \lambda_2 \leq \ldots \leq \delta_{n-1} \leq \lambda_n λ1≤δ1≤λ2≤…≤δn−1≤λn
根据这个事实,再用归纳法就可以推出上面式子。
分隔定理的证明(《代数特征值问题》p98)
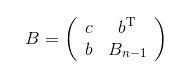
存在正交变换 Q Q Q,使得 Q T B Q Q^{\mathrm{T}}BQ QTBQ右下角变为对角阵。若正交矩阵 S S S使得 S T B n − 1 S S^{\mathrm{T}}B_{n-1}S STBn−1S为对角阵,那么,

且右下角矩阵的特征值并没有变化。
令:
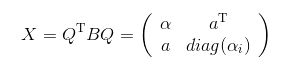
设 a a a只有 s s s个成分不为0,若 a j = 0 a_j=0 aj=0,那么 α j \alpha_j αj就是 X X X的特征值。
经过一个适当的置换矩阵 P P P变换,我们可以得到:
(注意,下面的 b b b和上面的 b b b不是一个 b b b,只是为了与书上的符号相一致)
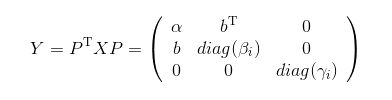
那么只需要考虑

的特征值就行了,因为 γ i \gamma_i γi是矩阵 A A A和 A n − 1 A_{n-1} An−1所共有的。
考虑 Z Z Z的特征多项式:
( α − λ ) ∏ i = 1 s ( β i − λ ) − ∑ j = 1 s b j 2 ∏ i ≠ j ( β i − λ ) = 0 (\alpha-\lambda)\mathop{\prod}\limits_{i=1}^{s}(\beta_i-\lambda)- \mathop{\sum}\limits_{j=1}^{s}b_j^2\mathop{\prod}\limits_{i \neq j}(\beta_i-\lambda)=0 (α−λ)i=1∏s(βi−λ)−j=1∑sbj2i̸=j∏(βi−λ)=0
假定 β i \beta_i βi中只有 t t t个不同的值,不失一般性,可令它们为 β 1 , β 2 , … , β t \beta_1,\beta_2,\ldots,\beta_t β1,β2,…,βt,
且重数为 r 1 , r 2 , … , r s ∑ i r i = s r_1,r_2,\ldots,r_s \quad \mathop{\sum}\limits_{i}r_i=s r1,r2,…,rsi∑ri=s
等式左端有因子:
∑ i = 1 t ( β i − λ ) r i − 1 \mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i-1} i=1∑t(βi−λ)ri−1
因此, β i \beta_i βi为 Z Z Z的特征值,重数为 r i − 1 r_i-1 ri−1
等式除以 ∑ i = 1 t ( β i − λ ) r i \mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i} i=1∑t(βi−λ)ri可得:
0 = ( α − λ ) − ∑ i = 1 t c i 2 ( β i − λ ) − 1 = a − f ( λ ) 0=(\alpha-\lambda)- \mathop{\sum}\limits_{i=1}^{t}c_i^2(\beta_i-\lambda)^{-1} =a-f(\lambda) 0=(α−λ)−i=1∑tci2(βi−λ)−1=a−f(λ)
Z Z Z的剩余的特征值是 a − f ( λ ) = 0 a-f(\lambda)=0 a−f(λ)=0的根。
根据正负的特点,和连续函数(实质上是分段的)根的存在性定理,可以知道
a − f ( λ ) a-f(\lambda) a−f(λ)的 t + 1 t+1 t+1个根 δ i \delta_i δi满足:
δ 1 > β 1 > δ 2 > … > β t > δ t + 1 \delta_1>\beta_1>\delta_2>\ldots>\beta_t>\delta_{t+1} δ1>β1>δ2>…>βt>δt+1
这样所有根的序列就得到了,就是我们要证的。整理一下可以得到,
除了刚刚讲的 t + 1 t+1 t+1个根,
还有 s − t s-t s−t个 β i \beta_i βi相同的特征值,以及
n − s − 1 n-s-1 n−s−1个 γ i \gamma_i γi.
另外一个性质
算法
我的理解这样的:
step1.选第一个特征,就是对角元最大的那个
step2.在第一个的基础上,再选一个,这次会形成一个 2 × 2 2\times2 2×2的子矩阵,所以,需要选择令这个矩阵首特征值最大的第二个特征。
step3.反复进行,直到k?
这是前向的,还有对应的后向的,一个个减。论文推荐是,俩种都进行,然后挑二者中比较好的一个。
未免太复杂了些?
代码
只写了前向的代码:
import numpy as np
def You_eig_value(C): #幂法 只输出特征值
d = C.shape[1]
x1 = np.random.random(d)
while True:
x2 = C @ x1
x2 = x2 / np.sqrt(x2 @ x2)
if np.sum(np.abs(x2-x1)) < 0.0001:
break
else:
x1 = x2
return x1 @ C @ x1
def forward(C):
n = C.shape[0]
label1 = set(range(n))
label = [np.argsort(np.diag(C))[-1]]
label1 -= set(label)
count = 0
while len(label1) > 0:
count += 1
maxvalue = 0
maxi = -1
for i in label1:
value = You_eig_value(C[label+[i],:][:,label + [i]])
if value > maxvalue:
maxvalue = value
maxi = i
label.append(maxi)
label1 -= {maxi}
return label
f = open('C:/Users/biiig/Desktop/pitprops.txt')
C = []
for i in f:
C.append(list(map(float, i.split())))
f.close()
C = np.array(C)
forward(C) # [12, 6, 5, 9, 1, 0, 8, 7, 3, 2, 11, 4, 10]
![Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]_第2张图片](http://img.e-com-net.com/image/info8/d25c4fff895c43dbb1f9cf9c5e6d699e.jpg)
![Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]_第3张图片](http://img.e-com-net.com/image/info8/80f604d8212945338502a0f75866e611.jpg)
![Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]_第4张图片](http://img.e-com-net.com/image/info8/eaba757c314942b3abd2845e0cf1ccbb.jpg)