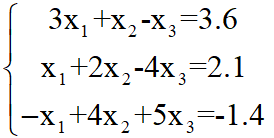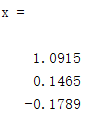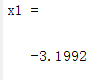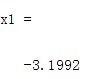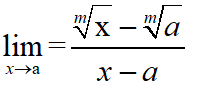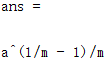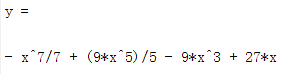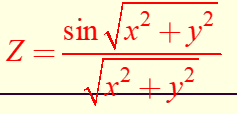Matlab自学笔记

Matlab自学笔记之入门整理

Matlab求解线性方程组的根

求解线性方程组（Ax=b形式）

方法一、

clear                                              
clc
A=[3 1 -1;1 2 -4; -1 4 5];
b=[3.6;2.1;-1.4];
x=A\b       

方法二、

clear
clc
A=[3 1 -1;1 2 -4; -1 4 5];
b=[3.6;2.1;-1.4];
% x=A\b
x=inv(A)*b%求A的逆矩阵并与b相乘

结果：

Matlab求解一元多次方程

%方法一
clear
clc
p=[2 0 3 71 -9 13];
x=roots(p)

%方法2
% 利用单变量非线性方程组求根函数
clear
clc
f=@(x)2*x^5+3*x^3+71*x^2-9*x+13;
x1=fzero(f,0)

%方法3
% 利用最优化工具箱方程求根函数

clear
clc
f=@(x)2*x^5+3*x^3+71*x^2-9*x+13;
x1=fsolve(f,-3,optimset('display','off'))%在-3附近搜寻x的最优值

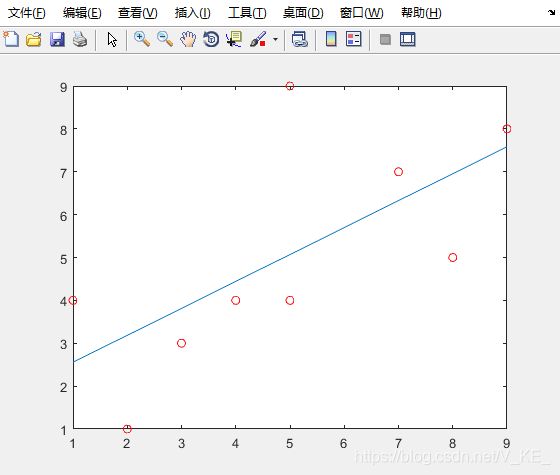
Matlab进行曲线拟合

%曲线拟合
% 理论上9个点最多可以拟合成8次曲线
clear
clc
x=[1 3 7 4 5 2 9 5 8];
y=[4 3 7 4 9 1 8 4 5];
p1=polyfit(x,y,1)%polyfit用来将已知点拟合称为一个多项式的形式
line=polyval(p1,x)%多项式在x处的值line
plot(x,line,x,y,'ro')

Matlab进行符号运算（求极限、定积分、不定积分）

% 符号运算
clear
clc
syms x a m;
y=(x^(1/m)-a^(1/m))/(x-a);
limit(y,x,a)%求解当x趋近于a时的极限

% 符号运算
clear
clc
syms x;
f=(3-x^2)^3;
y=int(f,x)%int用来求解定积分与不定积分如果想求定积分则可以写成int(f,x,积分下限,积分上限）的形式

Matlab进行二维绘图

% 二维绘图
clear
clc
x=0:0.2:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'r+-',x,y2,'bp:')

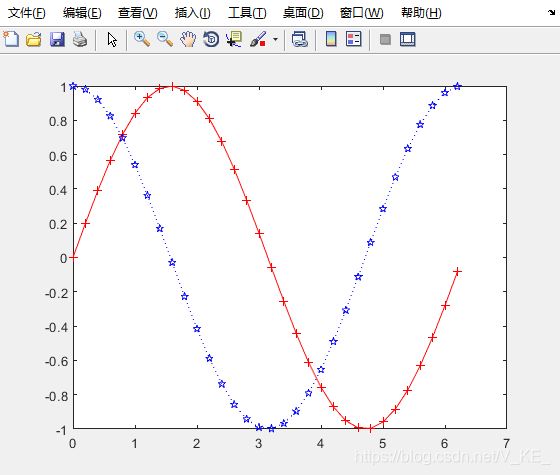
画图常用符号和颜色
转自https://blog.csdn.net/sinat_21026543/article/details/80215281
特别感谢

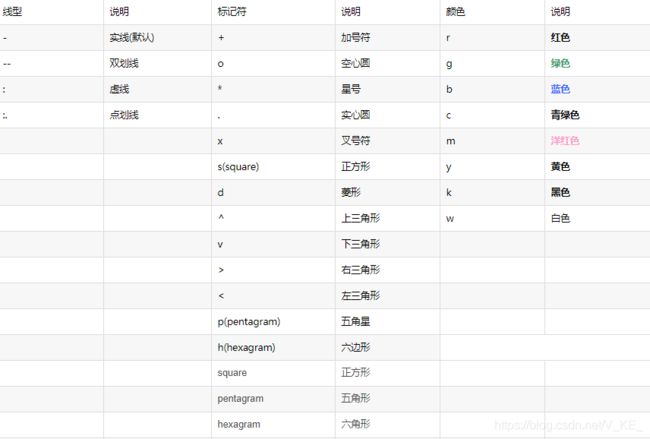
注：点划线为-.

Matlab进行三维绘图

plot3（x,y,z,'参数')
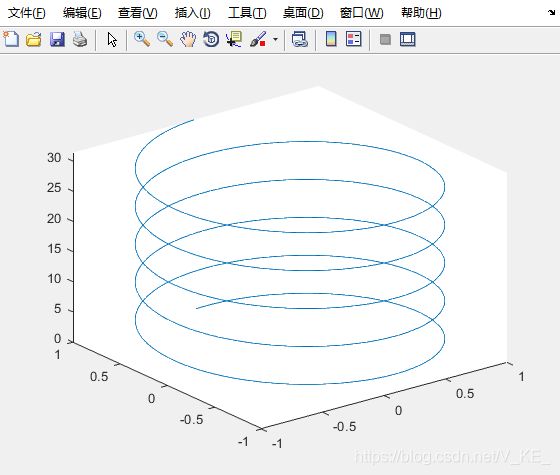
% 三维绘图
clear
clc
z=0:0.02:10*pi;
x=sin(z);
y=cos(z);
plot3(x,y,z)

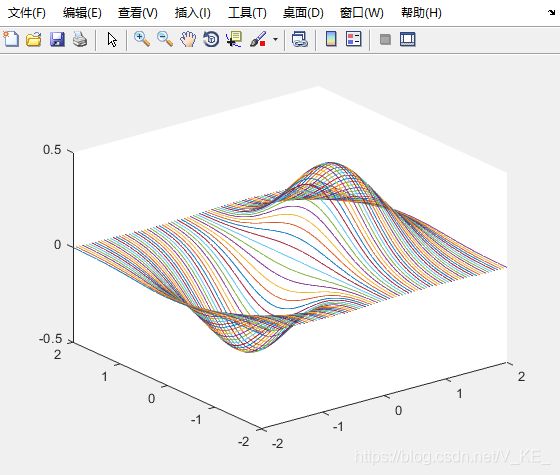
% 三维绘图
clear
clc
x=-2:0.05:2;
y=-2:0.05:2;
[X,Y]=meshgrid(x,y)
z=X.*exp(-X.^2-Y.^2);
plot3(X,Y,z)

meshgrid将等长度向量a，b转换为二维网格数据。

一些绘制三维曲线的相关命令函数

• plot3绘制三维曲线图形
• mesh绘制三维网格曲面
• meshc绘制带等高线的三维网格曲面
• meshz绘制带底座的三维网格曲面
• surf绘制填充颜色的三维网格曲面
  

% 三维绘图
clear
clc
X=-10:0.2:10;
Y=-10:0.2:10;
[x,y]=meshgrid(X,Y);
z=(sin(sqrt(x.^2+y.^2)))./(sqrt(x.^2+y.^2));
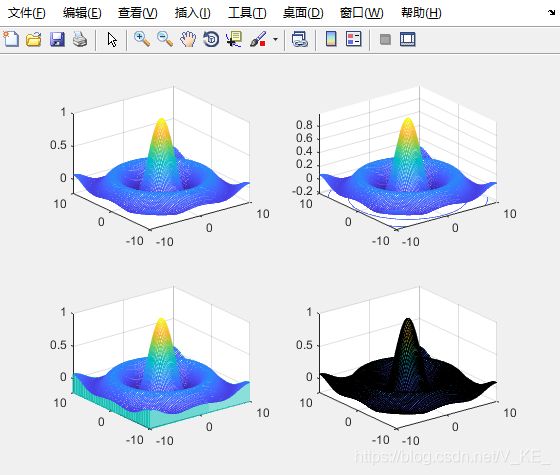
subplot(221)
mesh(x,y,z)%绘制三维网格曲面
subplot(222)
meshc(x,y,z)%绘制带等高线的三维网格曲面
subplot(223)
meshz(x,y,z)%绘制带底座的三维网格曲面
subplot(224)
surf(x,y,z)%绘制填充颜色的三维网格曲面