数据结构--DAG拓扑排序

一、引言

• 在学习拓扑排序之前，应该已经掌握了图的两种遍历方式 + 堆栈、队列的特点。
• 此文的实现，我会用Java实现。
• 蓝色表示细节，红色表示重要。

二、拓扑排序概念

1.在图中有一个重要的有向图类型，（有向图的表示方法仍然可以是邻接表或者邻接矩阵法）。

2.仅有有向图无环图才具备可以得到拓扑排序的序列。

3.进行拓扑排序有两种方式：

• 利用图的DFS遍历，记住顶点退出遍历栈的顺序，将该顺序列反过来就是拓扑排序的一个解。
• 利用减治算法，在图中找一个没有输入边的顶点，记录下来并删除，然后下一次执行同样操作，直到删除所有节点。

三、理论讲解

PS：这里会详细介绍上述的两种拓扑排序的方式

1.DFS回溯法

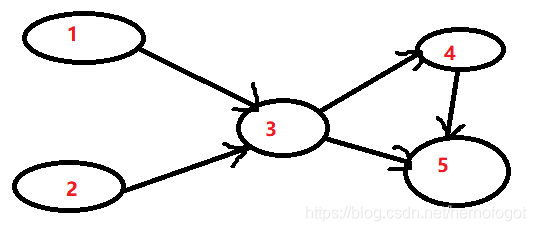
• 有如下有向无环图

• 利用DFS进行遍历可得遍历栈的顺序：５，４，３，１　２　（注意是否有逗号）
• 即出栈次序：５４３１２
• 可以得拓扑排序的序列之一为：２　１　３　４　５　，（注意遍历邻顶点时的随机性）　

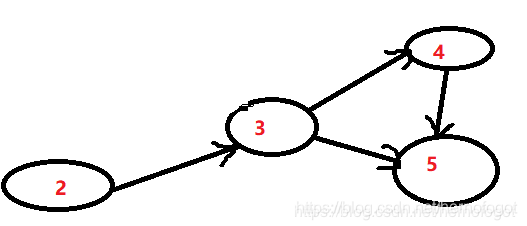
2. 减治法

• 首先删除没有输入边的节点 1，
• 然后删除 2 
• 删除 3                         
• 删除 4                 

   

• 删除5 得到：　１　2    ３　４　５

PS：可能会有人觉得两个结果怎么会不一样，这就时上面提到的随机性，先选择节点1和2 会得到不同的结果，其余节点有可能会发生这种情况，也就是说：拓扑排序和DFS一样序列可能有多个。

四、代码实例

PS：此处是转载 https://github.com/wangkuiwu/datastructs_and_algorithm/blob/master/source/graph/topsort/dag/java/ListDG.java

• 此处是利用DFS遍历进行拓扑排序的方式，另一种比较简单，留给读者思考哦

 

import java.io.IOException;
import java.util.Scanner;
import java.util.List;
import java.util.ArrayList;
import java.util.Queue;
import java.util.LinkedList;

public class ListDG {
    // 邻接表中表对应的链表的顶点
    private class ENode {
        int ivex;       // 该边所指向的顶点的位置
        ENode nextEdge; // 指向下一条弧的指针
    }

    // 邻接表中表的顶点
    private class VNode {
        char data;          // 顶点信息
        ENode firstEdge;    // 指向第一条依附该顶点的弧
    };

    private List mVexs;  // 顶点数组


    /*
     * 创建图(自己输入数据)
     */
    public ListDG() {

        // 输入"顶点数"和"边数"
        System.out.printf("input vertex number: ");
        int vlen = readInt();
        System.out.printf("input edge number: ");
        int elen = readInt();
        if ( vlen < 1 || elen < 1 || (elen > (vlen*(vlen - 1)))) {
            System.out.printf("input error: invalid parameters!\n");
            return ;
        }

        // 初始化"顶点"
        mVexs = new ArrayList();
        for (int i = 0; i < vlen; i++) {
            System.out.printf("vertex(%d): ", i);
            // 新建VNode
            VNode vnode = new VNode();
            vnode.data = readChar();
            vnode.firstEdge = null;
            // 将vnode添加到数组mVexs中
            mVexs.add(vnode);
        }

        // 初始化"边"
        //mMatrix = new int[vlen][vlen];
        for (int i = 0; i < elen; i++) {
            // 读取边的起始顶点和结束顶点
            System.out.printf("edge(%d):", i);
            char c1 = readChar();
            char c2 = readChar();
            int p1 = getPosition(c1);
            int p2 = getPosition(c2);
            // 初始化node1
            ENode node1 = new ENode();
            node1.ivex = p2;
            // 将node1链接到"p1所在链表的末尾"
            if(mVexs.get(p1).firstEdge == null)
                mVexs.get(p1).firstEdge = node1;
            else
                linkLast(mVexs.get(p1).firstEdge, node1);
        }
    }

    /*
     * 创建图(用已提供的矩阵)
     *
     * 参数说明：
     *     vexs  -- 顶点数组
     *     edges -- 边数组
     */
    public ListDG(char[] vexs, char[][] edges) {

        // 初始化"顶点数"和"边数"
        int vlen = vexs.length;
        int elen = edges.length;

        // 初始化"顶点"
        mVexs = new ArrayList();
        for (int i = 0; i < vlen; i++) {
            // 新建VNode
            VNode vnode = new VNode();
            vnode.data = vexs[i];
            vnode.firstEdge = null;
            // 将vnode添加到数组mVexs中
            mVexs.add(vnode);
        }

        // 初始化"边"
        for (int i = 0; i < elen; i++) {
            // 读取边的起始顶点和结束顶点
            char c1 = edges[i][0];
            char c2 = edges[i][1];
            // 读取边的起始顶点和结束顶点
            int p1 = getPosition(edges[i][0]);
            int p2 = getPosition(edges[i][1]);

            // 初始化node1
            ENode node1 = new ENode();
            node1.ivex = p2;
            // 将node1链接到"p1所在链表的末尾"
            if(mVexs.get(p1).firstEdge == null)
                mVexs.get(p1).firstEdge = node1;
            else
                linkLast(mVexs.get(p1).firstEdge, node1);
        }
    }

    /*
     * 将node节点链接到list的最后
     */
    private void linkLast(ENode list, ENode node) {
        ENode p = list;

        while(p.nextEdge!=null)
            p = p.nextEdge;
        p.nextEdge = node;
    }

    /*
     * 返回ch位置
     */
    private int getPosition(char ch) {
        for(int i=0; i='a'&&ch<='z') || (ch>='A'&&ch<='Z')));

        return ch;
    }

    /*
     * 读取一个输入字符
     */
    private int readInt() {
        Scanner scanner = new Scanner(System.in);
        return scanner.nextInt();
    }

    /*
     * 深度优先搜索遍历图的递归实现
     */
    private void DFS(int i, boolean[] visited) {
        ENode node;

        visited[i] = true;
        System.out.printf("%c ", mVexs.get(i).data);
        node = mVexs.get(i).firstEdge;
        while (node != null) {
            if (!visited[node.ivex])
                DFS(node.ivex, visited);
            node = node.nextEdge;
        }
    }

    /*
     * 深度优先搜索遍历图
     */
    public void DFS() {
        boolean[] visited = new boolean[mVexs.size()];       // 顶点访问标记

        // 初始化所有顶点都没有被访问
        for (int i = 0; i < mVexs.size(); i++)
            visited[i] = false;

        System.out.printf("== DFS: ");
        for (int i = 0; i < mVexs.size(); i++) {
            if (!visited[i])
                DFS(i, visited);
        }
        System.out.printf("\n");
    }

    /*
     * 广度优先搜索（类似于树的层次遍历）
     */
    public void BFS() {
        int head = 0;
        int rear = 0;
        int[] queue = new int[mVexs.size()];            // 辅组队列
        boolean[] visited = new boolean[mVexs.size()];  // 顶点访问标记

        for (int i = 0; i < mVexs.size(); i++)
            visited[i] = false;

        System.out.printf("== BFS: ");
        for (int i = 0; i < mVexs.size(); i++) {
            if (!visited[i]) {
                visited[i] = true;
                System.out.printf("%c ", mVexs.get(i).data);
                queue[rear++] = i;  // 入队列
            }

            while (head != rear) {
                int j = queue[head++];  // 出队列
                ENode node = mVexs.get(j).firstEdge;
                while (node != null) {
                    int k = node.ivex;
                    if (!visited[k])
                    {
                        visited[k] = true;
                        System.out.printf("%c ", mVexs.get(k).data);
                        queue[rear++] = k;
                    }
                    node = node.nextEdge;
                }
            }
        }
        System.out.printf("\n");
    }

    /*
     * 打印矩阵队列图
     */
    public void print() {
        System.out.printf("== List Graph:\n");
        for (int i = 0; i < mVexs.size(); i++) {
            System.out.printf("%d(%c): ", i, mVexs.get(i).data);
            ENode node = mVexs.get(i).firstEdge;
            while (node != null) {
                System.out.printf("%d(%c) ", node.ivex, mVexs.get(node.ivex).data);
                node = node.nextEdge;
            }
            System.out.printf("\n");
        }
    }

    /*
     * 拓扑排序
     *
     * 返回值：
     *     -1 -- 失败(由于内存不足等原因导致)
     *      0 -- 成功排序，并输入结果
     *      1 -- 失败(该有向图是有环的)
     */
    public int topologicalSort() {
        int index = 0;
        int num = mVexs.size();
        int[] ins;               // 入度数组
        char[] tops;             // 拓扑排序结果数组，记录每个节点的排序后的序号。
        Queue queue;    // 辅组队列

        ins   = new int[num];
        tops  = new char[num];
        queue = new LinkedList();

        // 统计每个顶点的入度数
        for(int i = 0; i < num; i++) {

            ENode node = mVexs.get(i).firstEdge;
            while (node != null) {
                ins[node.ivex]++;
                node = node.nextEdge;
            }
        }

        // 将所有入度为0的顶点入队列
        for(int i = 0; i < num; i ++)
            if(ins[i] == 0)
                queue.offer(i);                 // 入队列

        while (!queue.isEmpty()) {              // 队列非空
            int j = queue.poll().intValue();    // 出队列。j是顶点的序号
            tops[index++] = mVexs.get(j).data;  // 将该顶点添加到tops中，tops是排序结果
            ENode node = mVexs.get(j).firstEdge;// 获取以该顶点为起点的出边队列

            // 将与"node"关联的节点的入度减1；
            // 若减1之后，该节点的入度为0；则将该节点添加到队列中。
            while(node != null) {
                // 将节点(序号为node.ivex)的入度减1。
                ins[node.ivex]--;
                // 若节点的入度为0，则将其"入队列"
                if( ins[node.ivex] == 0)
                    queue.offer(node.ivex);    // 入队列

                node = node.nextEdge;
            }
        }

        if(index != num) {
            System.out.printf("Graph has a cycle\n");
            return 1;
        }

        // 打印拓扑排序结果
        System.out.printf("== TopSort: ");
        for(int i = 0; i < num; i ++)
            System.out.printf("%c ", tops[i]);
        System.out.printf("\n");

        return 0;
    }

    public static void main(String[] args) {
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        char[][] edges = new char[][]{
                {'A', 'G'},
                {'B', 'A'},
                {'B', 'D'},
                {'C', 'F'},
                {'C', 'G'},
                {'D', 'E'},
                {'D', 'F'}};
        ListDG pG;

        // 自定义"图"(输入矩阵队列)
        //pG = new ListDG();
        // 采用已有的"图"
        pG = new ListDG(vexs, edges);

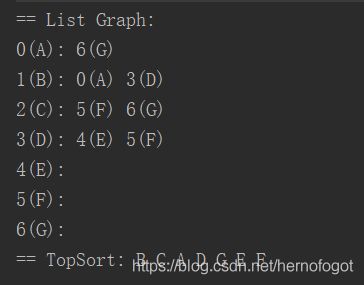
        pG.print();   // 打印图
        //pG.DFS();     // 深度优先遍历
        //pG.BFS();     // 广度优先遍历
        pG.topologicalSort();     // 拓扑排序
    }
}

 

 

执行的图和拓扑排序结果如下：

 

 

五、拓扑排序应用

1.拓扑排序通常用来“排序”具有依赖关系的任务。

比如，如果用一个DAG图来表示一个工程，其中每个顶点表示工程中的一个任务，用有向边 表示在做任务 B 之前必须先完成任务 A。故在这个工程中，任意两个任务要么具有确定的先后关系，要么是没有关系，绝对不存在互相矛盾的关系（即环路）。